“产生式”对数学概念定义理解教学的启示

杨召朋（江苏省南京市金陵中学龙湖分校）

“产生式”对数学概念定义理解教学的启示

杨召朋（江苏省南京市金陵中学龙湖分校）

良好数学认知结构的特征之一是具备稳定而又灵活的正向和逆向产生式.数学概念的定义都是关于概念的充要命题，定义作为概念的判断与性质在形式和实质上与正、逆向产生式一致.教师围绕产生式进行概念定义的理解教学，可以使学生更快、更好地掌握新知.

数学认知结构；特征分析；数学概念；产生式

著名数学教育专家曹才翰先生提出，数学认知结构，就是学生头脑里的数学知识按照自己的理解深度、广度，结合自己的感觉、知觉、记忆、思维、联想等认知特点，组合成的一个具有内部规律的整体结构.数学教学的根本任务在于造就学生良好的数学认知结构，以满足后继学习的需要，最终提高学生的问题解决能力.华南师范大学何小亚先生从问题解决出发，认为良好的数学认知结构的特征包括四个方面，即足够多的观念，具备稳定而又灵活的产生式，层次分明的观念网络结构，一定的问题解决策略等.这其中的“产生式”是指学习者在学习的过程中，其头脑里逐步贮存了一系列以“如果……，那么……”的形式表示的规则，这种规则称为产生式（production）（又称之为正向产生式），除此之外还有逆向产生式，是以“要……，就要……”的形式表示的规则，还有变形产生式（本文暂不讨论）等.显然，正、逆向产生式既可以帮助学生记忆所学知识要点，架构知识网络，又可以促使学生产生联想，变通使用知识，提升发散思维能力，培养学生分析和解决问题的能力.

一、定义作为概念的判定和性质的理解

学生对数学知识的学习往往都是从数学概念开始的，概念的定义则是揭示概念内涵的逻辑方法.一切定义都由被定义项（用DS表示）、定义项（用DP表示）和定义联项三部分组成.凡是定义，都是关于概念的充要命题，任何数学概念的定义都可由定义项得出被定义项（即概念的判定），理解成“如果DP，那么DS”的形式.也可由被定义项得出定义项（即概念的性质），理解成“如果DS，那么DP”的形式，此形式下分析问题思考成“要DP，就要DS”.这与正、逆产生式的规则一致.

例如，角平分线的定义是：把一个角分成两个相等角的射线叫做这个角的平分线.（1）定义作为判定.如图1，如果∠AOC＝∠BOC，那么OC是∠AOB的平分线.（2）定义作为性质.如图1，如果OC是∠AOB的平分线，那么

∠AOC＝∠BOC（分析问题时思考：要∠AOC＝∠BOC，就要OC是∠AOB的平分线）.

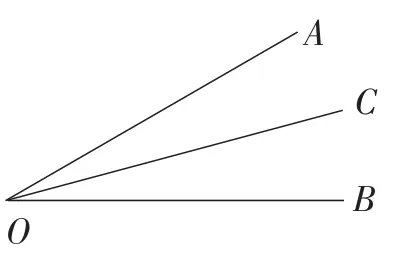
图1

学生掌握定义作为概念的判定和性质并不意味着已经具备相应的正、逆产生式.当学生看到图1及角平分线条件立即做出反应∠AOC＝∠BOC，此时该学生才具备产生式，而如果学生是被问到∠AOC与∠BOC的关系时才说出相等，则该学生并不一定具备产生式.逆向产生式则随着所掌握知识的增加而丰富.例如，要两角相等，就要角平分线（角平分线定义）或两边相等（等边对等角）或三角形全等（全等三角形的性质）或都等于另一角（等量代换）等.显然，具备稳定而又灵活的产生式越多，联想到的知识就可能越自然、越丰富，更利于理解和掌握更多的定义.

二、教学启示

1.感知产生式，加强明晰概念定义的结构

数学教育家徐利治先生认为，数学中的概念和方法都必须是构造性的.数学概念是构造的，其定义方式都是构造定义方式，这不仅能增强在学习上对数学的理解力，而且又可作为一种思维方式和方法.因此，学习数学新概念应抓住其定义的结构和本质属性，从中感知定义的产生式，再解决围绕定义设置的问题，弄清概念定义的结构，提高运用新定义的能力.

案例1：二次根式定义课堂建构活动.

活动1：填空：

（1）在Rt△ABC中，∠C=90°，AB=30 m，BC=am，则AC=_______.

（2）圆的面积为S，则该圆的半径是______.

（3）正方形的面积为b－1，则它的边长是____.

回答：上面三道题的结果中的代数式有什么共同特征？

活动2：你能给二次根式下个定义吗？

活动3：将二次根式的定义改写成“如果……，那么……”和“要……，就要……”的形式，并与同学交流.

活动4：独立完成：（1）找出下列各式中的二次根式：

上述建构活动引导学生从三个代数式的属性中得到二次根式定义中两个本质属性，即带二次根号和根号下的数（被开方数）不小于0.至于出现什么字母，来源于什么实际问题并不重要.在活动2、活动3中通过对定义的改写，可以得到产生式：如果一个代数式形如那么这个式子叫做二次根式；要使一个代数式是二次根式，就要这个式子满足的形式，进一步让学生明晰了结构，感受了产生式.活动所涉及的问题恰当地联系了数学概念的原型，有利于丰富学生的感性认识，激发起学生学习新定义的主动性和积极性.另外，教师会针对下节课的内容布置给学生预习作业，以便更好地开展教学，预习作业不应贪多求全，应贴合学生的最近发展区，围绕核心的基础知识，如概念的内涵而非外延.值得一提的是，当下的慕课、微课等，基本都配以讲解，最好不要让学生在预习时使用，否则会极大地削弱学生独立自主学习新定义的能力和意识.

2.领会产生式，关注运用类比思想释疑

类比是一种思维形式，是由两个或两类思考对象在某些属性上的相同或相似，从而推出它们在另一属性上也相同或相似的一种推理方法.有些概念的定义较为复杂和抽象，需要教师在课堂中着力去帮助学生理解和认识.运用类比，能找出可供与新概念对比的旧概念，指出它们各自定义的相同点和不同点，领会产生式，更好地理解新定义.

案例2：不等式的解的定义课堂教学片断.

师：什么叫方程的解？请举例说明.

生1：使方程左右两边相等的未知数的值叫做方程的解.例如，3是方程x－3=0的解.

师：很好，那通过昨天的预习，不等式的解又是怎样定义的呢？

生2：我自己的理解是使不等式左右两边不等关系成立的未知数的值.

师：自己的理解，好，那你为什么这么理解呢？

生2：我觉得它与方程的解的定义应该类似，因为它只是将“方程”换为“不等式”，“相等”换成“不等”而已.

师：（面向全体）说得很好，他用类比的方法，说出了它们的相同之处，那不同之处呢？

学生思考、交流.

生3：应该是解的个数不同.例如，x＋1＞3中的x值可以有3，4，5等，很多.

师：的确是这样.我们来看不等式的解的定义.

投影：使不等式成立的未知数的值叫做不等式的解.

师：在定义中，如果未知数的一个取值使得不等关系成立，那么这个值就叫做不等式的解.反之，要求不等式的解，就要找使不等关系成立的未知数的值.

至此，学生通过对比不难认识到：方程的解是使方程左右两边相等的未知数的值，不等式的解是使其成立的未知数的取值范围.从使原式成立来看，方程的解与不等式的解的意义是一致的.显然，教师最后对定义作为概念的判定和性质的剖析起到了画龙点睛的作用，学生在此基础上，领会了定义的产生式，也建构了定义，更由此推测，在数轴上方程的解是数轴上的一个或几个点，不等式的解则是无数个点.

3.强化产生式，突出应用概念定义的范例解读

例题是数学知识转化为基本技能的附体，揭示解题的思路和方法，通过例题的学习，可以理解和巩固数学基础知识.在概念教学中应突出定义的应用示范，选择可直接利用定义解题的例题，引导学生对概念定义的理解，强化学生对其产生式的认识，提升学生阅读理解和自主学习的能力.

案例3：一道范例的解题过程.

例重心有很多美妙的性质，如有关线段比、面积比就有一些“漂亮”结论，试完成如下问题.

（1）若O是△ABC的重心（如图2），连接AO并延长交BC于点D，证明：

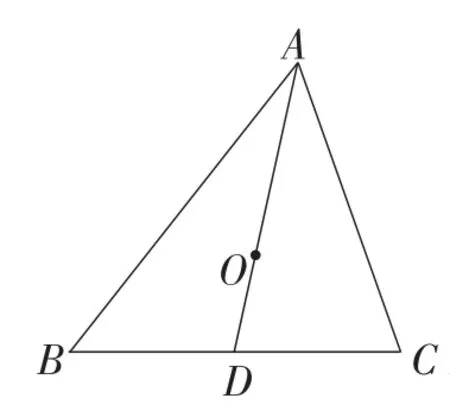
图2

（2）若AD是△ABC的一条中线（如图3），O是AD上一点，且满足试判断点O是△ABC的重心吗？如果是，给出证明过程；如果不是，说明理由.

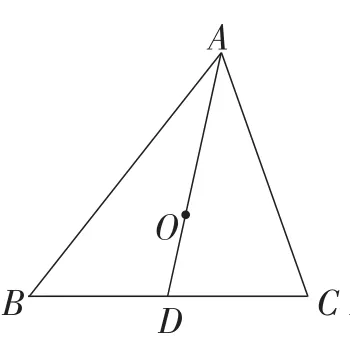
图3

（3）若O是△ABC的重心，过点O的一条直线分别与AB，AC相交于点G，H（均不与△ABC的顶点重合，如图4），S四边形BCHG，S△AGH分别表示四边形BCHG和△AGH的面积，试探究的最大值.

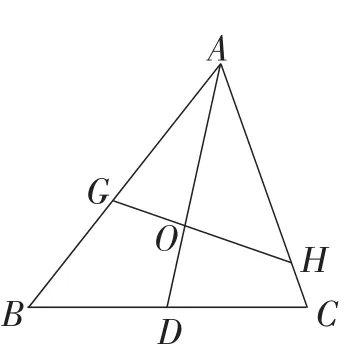
图4

分析：《义务教育数学课程标准（2011年版）》添加了三角形重心的概念.第（1）小题是正向产生式：如果点O是△ABC的重心，那么△ABC的三条中线交于一点；第（2）小题是逆向产生式：要点O是△ABC的重心，就要△ABC的三条中线交于一点.第（3）小题略.

解：（1）如图5，连接CO并延长交AB于点P，连接PD.

因为点O是△ABC的重心，所以P是AB的中点.

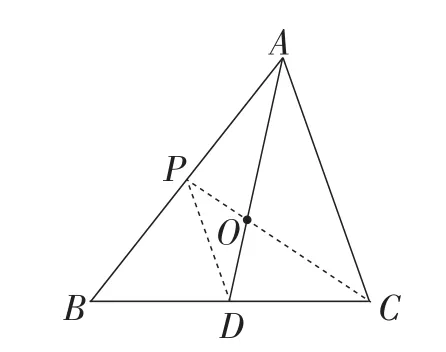
图5

可得AC∥PD.

所以△OPD∽△OCA.所以

（2）如图6，作△ABC的中线CP，与AB边交于点P，与△ABC的另一条中线AD交于点Q，

则点Q是△ABC的重心.

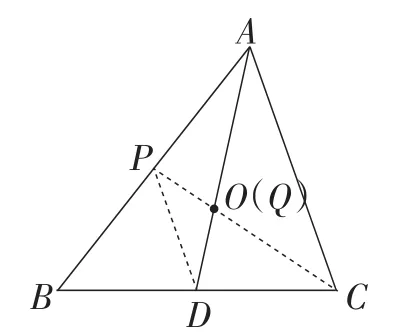
图6

所以点Q与点O重合（是同一个点）.

所以点O是△ABC的重心.

（3）略.

学生对新知识的接纳有个吸收和消化的过程，利用新学定义直接解决问题，可以让学生体会到解题关键在于对定义的正确认识和理解.这既可以提升学生的学习兴趣，积极地把习得的方法和形成的能力迁移到新定义中，又可以创造应试的氛围，让学生深刻理解定义的产生式对解决新问题的影响和作用.而学生对定义的分析和应用能力并非一日养成，平时对教材中每一个新概念的预习和学习正是能力培养的最佳时机.

4.迁移产生式，重视设置悬念拓展概念

悬念是欣赏戏剧、电影或者其他文艺作品时的一种心理活动，即关切故事发展和人物命运的紧张心情.在教学中设置悬念则是在知识的某一部分设置疑问或矛盾冲突，激发学生的探索兴趣.教师在学生已经理解相关概念并巩固后，应在课堂小结的环节对定义进行拓展，恰当设置悬念，突出对产生式的迁移，帮助学生举一反三、触类旁通，为后续学习打下基础.

案例4：一次函数概念的课堂小结教学片断.

师：下面我们对本节课知识做一个小结.

投影1：如果一个函数的表达式为y＝3x－1，那么它是____函数.

投影2：（1）要使一个函数是正比例函数，它的表达式就要符合的______形式，如_____；

（2）如果要给二次函数和反比例函数下定义，你会怎么做？

生：我觉得不难吧，因为二次函数与一次函数只是一字之差，这让我想到一元二次方程与一元一次方程的定义的联系和区别.

师：很对，大家可以尝试解决这个问题.

教师在课堂中带领学生进行小结，在学生以为知识的学习即将翻篇时，设置悬念激发起学生的学习兴趣和主动性，使其在新的高度上把握所学定义，达到迁移产生式，拓展概念的目的.例如，教材中知识的呈现是螺旋式上升的，苏科版教材在八年级上册中安排了一次函数，八年级下册中安排了反比例函数，而二次函数则被安排在九年级下册，这就为学生知识的积淀和能力的提升提供了操作和思维空间.教师在学生学习了一次函数及正比例函数后，让学生分别尝试定义反比例函数、二次函数，并探究它们的图象和性质.

数学概念的学习是整个数学学习的前提和重要环节，概念定义的学习则是概念学习的必经之路，首当其冲.正所谓，好雨知时节，……，润物细无声.由良好数学认知结构中的正、逆产生式做引导，强化概念定义的正、逆产生式教学，不仅有助于增强学生在定义学习上对知识的理解能力和应用能力，把概念更好地按自己的理解深入、拓宽，更可将由产生式学习新知作为一种思维方式，学会从感觉、知觉、联想等去认知.逐步将上述思维方式用在基本事实、定理、公式、法则等知识的学习上，形成由因及果、执果索因的意识和能力，帮助学生更好地理解和掌握新知识，不断促使学生更快、更好地构建良好数学认知结构.

［1］曹才翰，蔡金法.数学教育概论［M］.江苏：江苏教育出版社，1989.

［2］潘玉恒，杨珂玲.论数学概念的定义方式［J］.数学教育学报，2012，21（4）：32-35.

［3］沈吉波.“无理数”概念教学思考：由一道错例引发的思考［J］.中学教学参考（中旬），2012（8）：11-12.

2016—09—08

杨召朋（1979—），男，中学一级教师，主要从事初中数学教学研究.