一类分块形式的范德蒙行列式的求值

郑志熳，何超林，吴康

（华南师范大学数学科学学院，广东广州510631）

一类分块形式的范德蒙行列式的求值

郑志熳，何超林，吴康

（华南师范大学数学科学学院，广东广州510631）

对范德蒙行列式进行了推广，定义了一类分块形式的范德蒙行列式，并运用行列式的性质，分块矩阵的运算和技巧，Laplace展开定理以及对称多项式的性质，得出该类分块形式的范德蒙行列式的求值计算公式.

分块形式的范德蒙行列式；行列式的性质；分块矩阵的运算；Laplace展开定理；对称多项式

0 引言

范德蒙德行列式是线性代数中一个很重要的行列式.在数学领域中，范德蒙行列式在行列式计算、微积分、多项式理论、线性变换理论、向量空间理论等方面都有广泛的应用；在其他工程技术领域如计算机技术、自动化技术等也有许多应用.如：文献[1-4]研究第二、三、四类的广义范德蒙行列式，并得出其化简求值的结果；文献[5-11]对范德蒙行列式进行再推广并得到相关的计算公式，依次研究最后一行元素次数为m（m为大于阶数的正整数）的第二类范德蒙行列式，第k（k为正整数）类广义范德蒙行列式，连续缺m（m为小于阶数的正整数）行的广义范德蒙行列式，间断缺m（m为小于阶数的正整数）行的广义范德蒙行列式，每一行的次数为互不相关的正整数的广义范德蒙行列式，合流范德蒙行列式；文献[12-13]分别研究E-范德蒙行列式，分块形式的范德蒙行列式（准范德蒙行列式）.然而在分块形式的范德蒙行列式这方面的研究基本没有继续深入.本文在前面所述研究的基础上，利用分块矩阵的运算和范德蒙类行列式的良好性质，对缺一行的分块形式的范德蒙行列式（准-跳行范德蒙行列式）进行了研究，并得出其求值计算公式.

1 预备知识

1.1 定义说明

定义1设Aj（j＝1，2，3，…，n）为m阶方阵（m，n∈N*），E为m阶单位矩阵，则称

为n阶缺第i＋1行的准-跳行范德蒙行列式，其中1≤i≤n－1且i∈N*，约定.

定义2设Ak，Ak＋1，…，Ak＋i－1为两两可交换的m阶方阵（k∈N，m，i∈N*），定义矩阵的以Ak为首项的i元j次对称多项式为：

其中j∈N，约定Mk（i，0）＝E.

定义3设Ak，Ak＋1，…，Ai为两两可交换的m阶方阵（m，k，i∈N*且k≤i），定义矩阵的i＋1－k元j次初等对称多项式为：

其中j∈N*，约定σj＝0（j＞k＋i-1）.

1.2 主要引理

引理1[11]设Aij（i，j＝1，2，3，…，n）和B均为m阶方阵（m是任意正整数，n∈N*），则

引理2[15]设A，B分别为r，s阶方阵，C为s×t矩阵，那么

引理3Mk（i，j）－Mk＋1（i，j）＝（Ak－Ak＋i）·Mk（i＋1，j－1）.（i∈N*，k，j∈N）

证明：由定义2知，

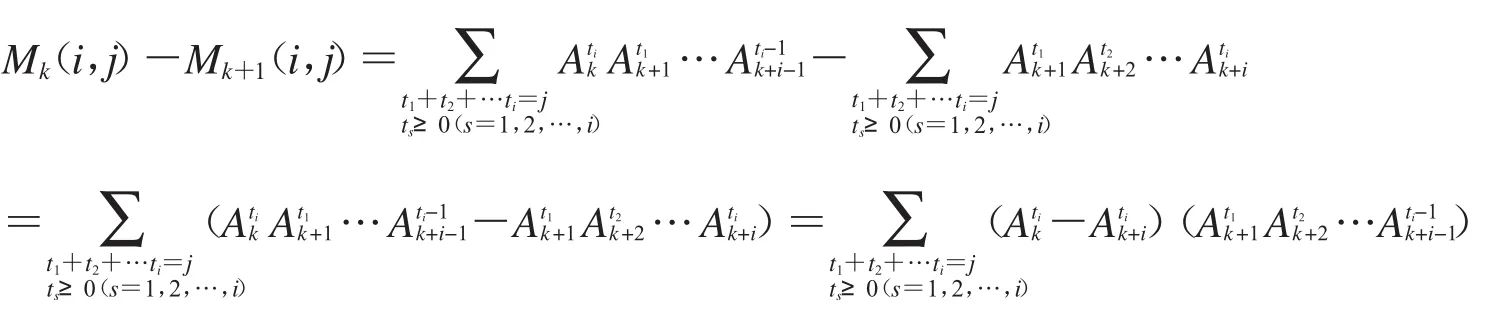
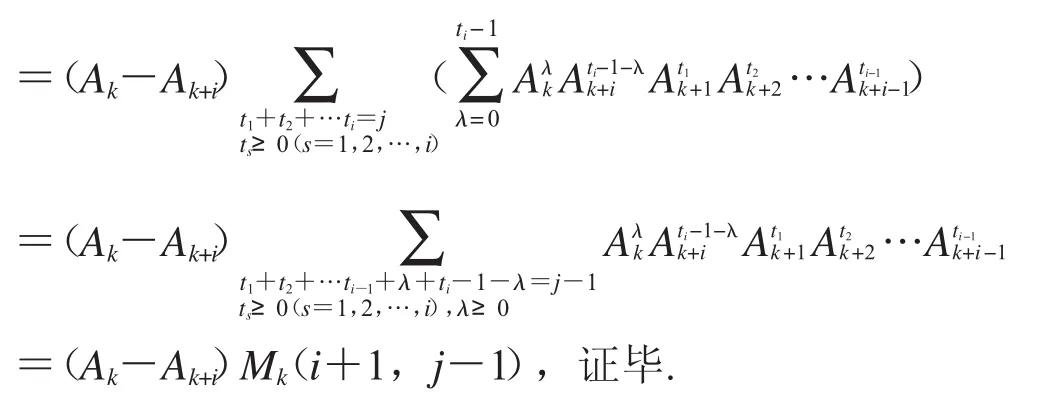
引理4[16]设Aij（i，j＝1，2，3，…，n）和B为m阶方阵（m，n∈N*），E为m阶单位矩阵，a，b＝1，2，3，…，n，则

引理5若E是m阶单位矩阵（m为任意正整数），A是[m（n-1）]×[m（n-2）]阶矩阵，B、C是[m（n-1）]×m阶矩阵，第一个O矩阵是m×[m（n-2）]阶矩阵，第二个O矩阵是m阶矩阵，则

证明：由Laplace展开定理可得.

注：由于引理6中的fk是在定理2中的推导过程中得到的，因此，本文把补充引理——引理6安排在定理2的证明过程中.

2 主要结论

定理1设Ai，Aj（i，j＝1，2，3，…，n）为两两可交换的m阶方阵（m，n∈N*），E为m阶单位矩阵，则

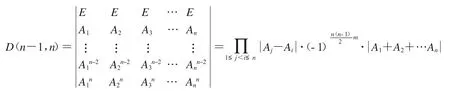
证明：由定义2知

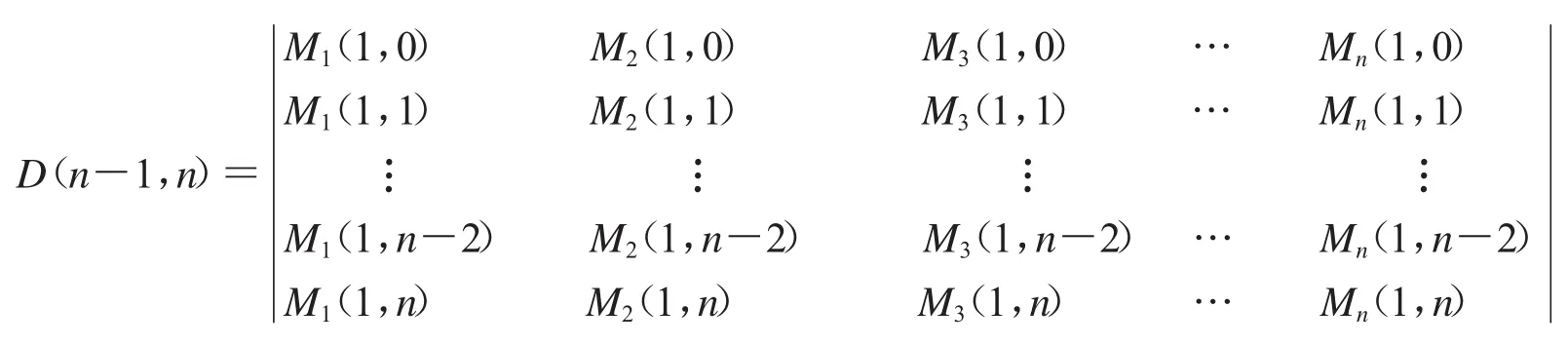
又由行列式性质得

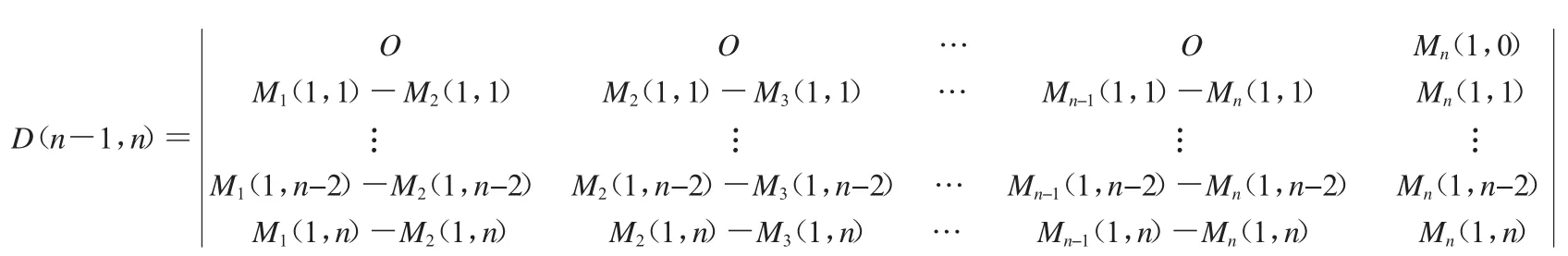
由引理1和引理3以及Ai，Aj（i，j＝1，2，3，…，n）两两可交换得

由引理2得

同理，以此类推有

定理2设Aa，Ab（a，b＝1，2，3，…，n）为两两可交换的m阶方阵（m，n∈N*），E为m阶单位矩阵，则

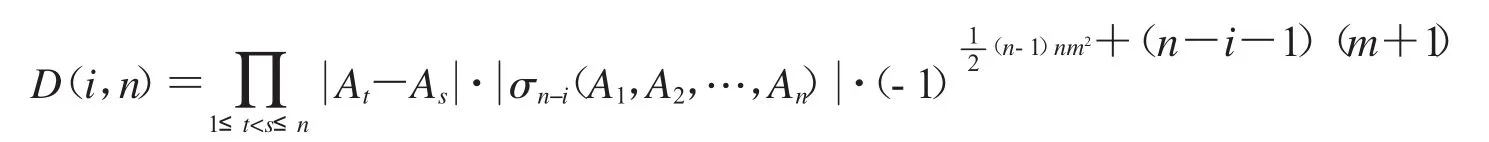
证明：由定义2有

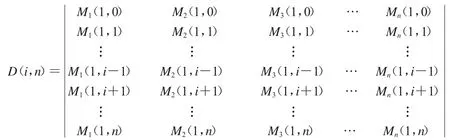
根据引理3和定理1，上式可化为含有n－i阶行列式的式子，如下：

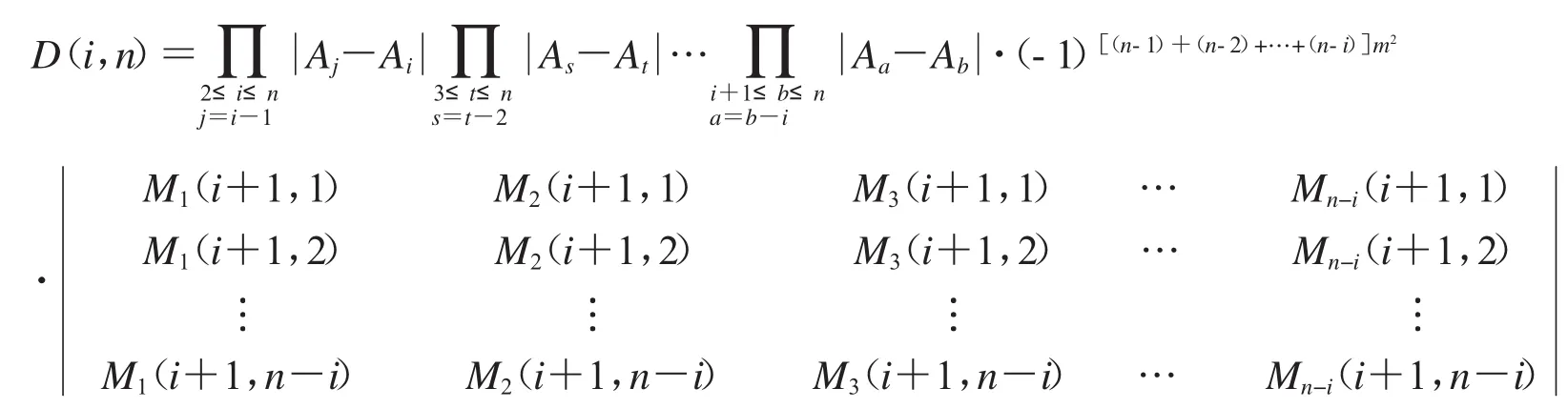
运用定理1的方法，相邻两列所对应的矩阵作差一次，由引理3和引理1得

此时，上式所得到的行列式的第一行除了最后一项的每个元素不再是零矩阵，而是单位矩阵，故前n－i－1列再次作差得

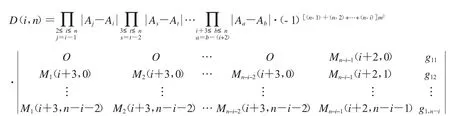
由引理4知，第n－i－1列乘以－g11加到第n－i列得

由引理5有

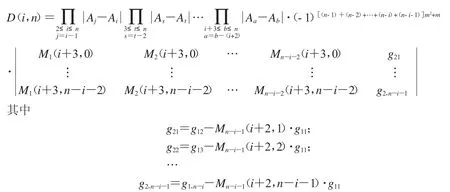
再由行列式性质，引理1和引理3得

由引理4知，第n－i－2列乘以－g21加到第n－i－1列，有

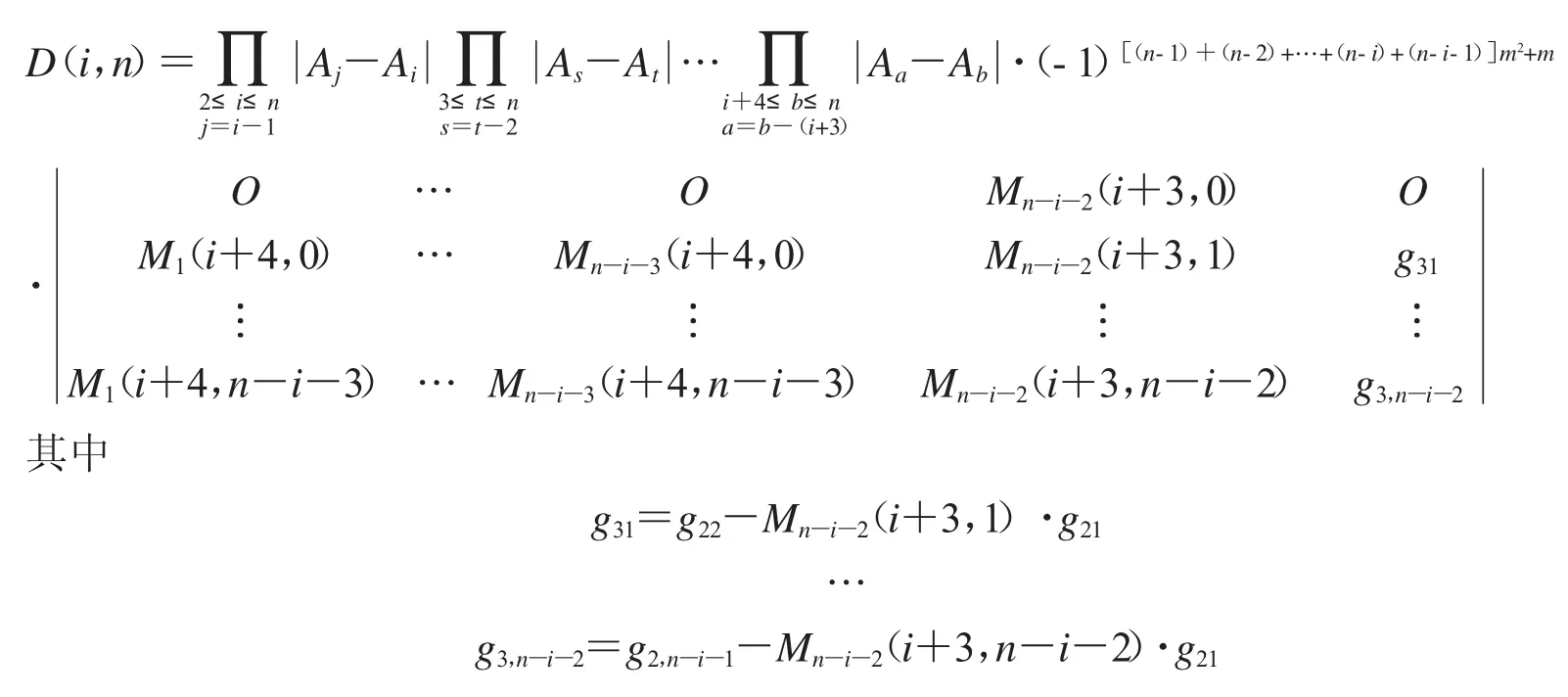
再由引理5有

令f1＝g11；f2＝g21；f3＝g31；…；fk＝gk1；…（k∈N*且1≤k≤n－i），则对上述fk有以下引理：

其中Mn－i（i＋1，k），Mn－i－t（i＋t＋1，k－t）均满足定义2，Aa，Ab（a，b＝n－i－t＋1，…，n）为两两可交换的m阶矩阵，m，n，i∈N*且1≤i≤n－1，k∈N*且1≤k≤n－i.

证明：要证

下面先证，n＝2，3时，对所有满足条件的i，k成立.

当n＝2时，i＝1，k＝1，左边＝M1（2，1）＝A1＋A2＝M0（3，1）·σ1（A1，A2）·（-1）0＝右边，命题成立；

当n＝3时，需证对于i＝0，k＝1，2和对于i＝1，k＝1时，命题成立；

当n＝3，i＝1，k＝1时，左边＝M2（2，1）＝A2＋A3＝M1（3，0）·σ1（A2，A3）·（-1）0＝右边；

当n＝3，i＝1，k＝2时，左边＝M2（2，2）＝A22＋A2A3＋A32

＝（A1＋A2＋A3）（A2＋A3）－（A1A2＋A1A3＋A2A3）

＝M1（3，1）·σ1（A2，A3）·（-1）0＋M0（3，0）·σ2（A1，A2，A3）·（-1）1＝右边；

当n＝3，i＝2，k＝1时，

左边＝M2（3，1）＝A1＋A2＋A3＝M1（4，0）·σ1（A1，A2，A3）·（-1）0＝右边；

所以，当n＝2，3时，对所有满足条件的i，k命题成立.

再证，若n＝n'时命题成立，则当n＝n'＋1时命题也成立.

假设n＝n'时命题成立，则

1）由D（i，n'）与D（i，n'+1）行列式的结构知，当n＝n'＋1时，

2）下证i＝n'，k＝n'＋1－i＝n'＋1－n'＝1时上式也成立.

当i＝n'，k＝1时，左边＝M1（n'＋1，1）＝A1＋A2＋A3＋…＋An'＋1

＝M0（n'＋2，0）·σ1（A1，A2，A3，…，An'＋1）·（-1）0＝右边；

对于1≤i≤n'，1≤k≤n'＋1－i成立.

故由1）和2）得，当n＝n'＋1时命题也成立.

从而由上述n＝2，3时对所有满足条件的i，k命题成立，由数学归纳法可得，对于任意正整数n（n≥3），命题成立.引理6证毕.

故由引理5知，fk＝σk（An－k－i＋1，…，An）（-1）k－1，故fn－i＝σn－i（A1，A2，…，An）（-1）n－i－1，通过递推可得，

定理2证毕.

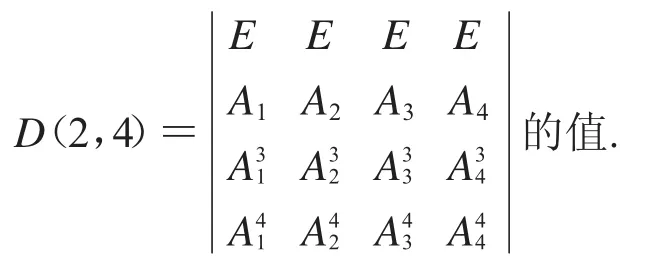
解：由A1，A2，A3，A4可交换及定理3得：

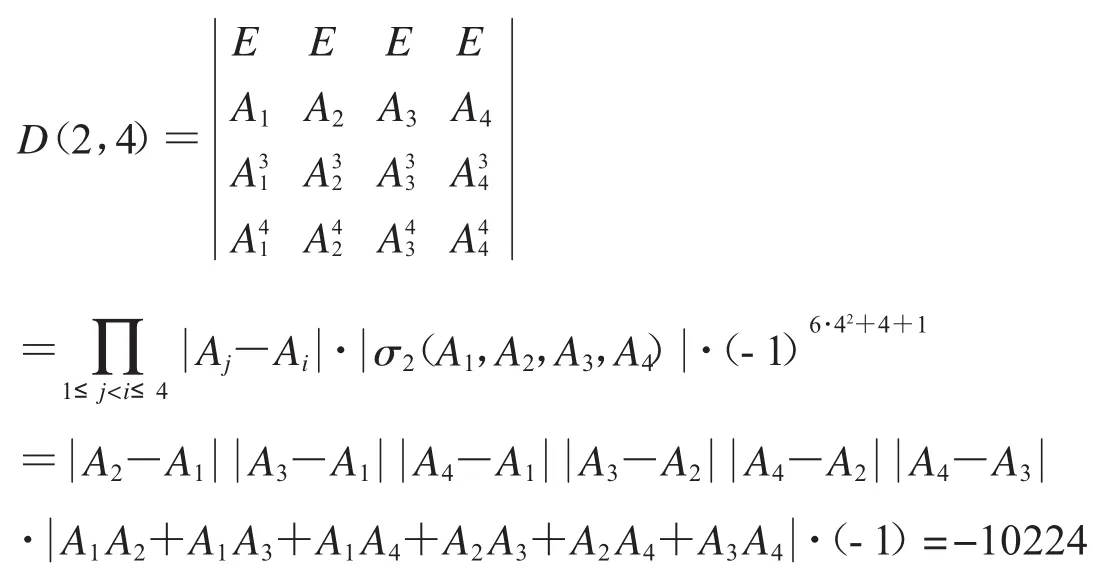
参考文献

[1]苏翃，邱利琼，田坚.二类广义Vandermonde行列式的计算[J].大学数学，2008，24（1）：135-137.

[2]陈祥恩，程辉，刘仲奎，等.第三类广义Vandermonde行列式的计算[J].大学数学，2012，28（1）：162-164.

[3]郭艳凤，张明俊，熊维玲.构造辅助函数计算准Vandermonde行列式[J].数学的实践与认识，2013，43（3）；254-259.

[4]何樱.第四类广义Vandermonde行列式的计算[J].浙江外国语学院学报，2013（4）：53-56.

[5]苏化明，潘杰.对一道线性代数习题的探讨[J].高等数学研究，2008，11（6）：13-15.

[6]汤健儿，范舒羽.广义范德蒙行列式[J].高等数学研究，2010，13（4）：48-49.

[7]蔡南莲.推广的范德蒙行列式的某些结果[J].集美大学学报（自然科学版），2013，18（4）：291-296.

[8]凌征球，廖珊莉.广义范德蒙行列式的定义及其计算[J].高师理科学刊，2015，35（9）：5-7.

[9]尤兰，王振.Vandermonde行列式的一类推广[J].科教文汇，2014（28）：49-50.

[10]李琳，陆全，徐仲，等.范德蒙类矩阵与合流范德蒙矩阵的行列式[J].数学的实践与认识，2009，39（10）：176-179.

[11]邱建霞.增次广义Vandermonde矩阵[J].大学数学，2005，21（3）：85-90

[12]刘长河.E-Vandermonde类方程组的快速算法[J].辽宁师范大学学报（自然科学版），2011，34（3）：272-277.

[13]齐登记.准Vandermonde行列式[J].合肥工业大学学报（自然科学版），2006，29（2）：254-256.

[14]张禾瑞，郝鈵新.高等代数[M].5版.北京：高等教育出版社，2007.

[15]张燕.分块矩阵行列式的性质及其应用[J].高等函授学报（自然科学版），2010，23（6）：31-33.

[16]张顺华.分块矩阵的性质及应用[J].山东水利专科学院学报，1992，4（1）：45-49.

Calculation of a K ind of Partitioned Vandermonde Determ inant

ZHENG Zhiman,HE Chaolin,WU Kang
（School of Mathematics,South China Normal University,Guangzhou 510631,Guangdong,China）

The calculation of Vandermonde Determinant is generalized,giving the definition of a kind of partitioned Vandermonde determinant.The calculating formula is obtained by using the property of determinant,methods and skills of partitioned matrices,Laplace expansion,and the property of symmetrical polynomial.

partitioned Vandermonde determinant;property of determinant;operation of partitioned matrices;Laplace expansion;symmetrical polynomial

O151.2

A

1001-4217（2016）04-0040-09

2015-11-11

郑志熳（1992—），女，汉，广东揭阳人，研究生在读，主要研究方向：数学教育；E-mail：444751832@qq.com