可拉伸梁方程一致紧吸引子的存在性

王素萍，邵旭馗

（陇东学院数学与统计学院，甘肃庆阳745000）

可拉伸梁方程一致紧吸引子的存在性

王素萍，邵旭馗

（陇东学院数学与统计学院，甘肃庆阳745000）

考虑了当外力项h满足条件C*（而非平移紧时），利用一致条件（C）证明了非自治可拉伸梁方程在强拓扑空间D（A）×V中一致紧吸引子的存在性.

可拉伸梁方程；一致条件（C）；条件C*；一致吸引子

0 引言

假设Ω⊂R2是具有光滑边界∂Ω的有界区域.本文将讨论并详细证明下面非自治的非线性梁方程

一致吸引子的存在性.其中α，β，γ，k均为正常数，h（x，t）和g（u）是外力项.若γ＝0，g（u）＝0且h（x，t）≡0，方程（1）由Woinowsky-Krieger在1950年提出，u（x，t）描述了可拉伸梁的横向偏斜.1973年，Ball[1]在文中讨论了这类问题解的存在性，唯一性，正则性及古典解的存在性，随后作者在文献[2]中利用拓扑方法及半群的弱连续性又获得了这类方程解的存在性及渐进性.而文献[3]给出了梁方程指数吸引子的存在性，文献[4-5]获得了梁方程在强拓扑空间中全局吸引子的存在性，文献[6]证明了可拉伸梁方程在弱拓扑空间E0＝V×H中的一致吸引子的存在性.类似问题的研究可参考文献[7-13].本文利用一致条件（C）证明方程（1）在强拓扑空间E1＝D（A）×V中一致紧吸引子的存在性.

1 预备知识

假设非线性函数g满足下面条件：存在常数C1＞0，使得

令H＝L2（Ω），，H和V的内积和范数分别用(·,·)，，它们的内积被分别定义为

根据Poincare不等式，我们有

定义1[7]若∑是一参数集，，σ∈∑称作Banach空间E上的过程族，如果是一个过程，即就是双参数的映射族从E到 E满足

定义2[8]过程族满足一致（关于σ∈∑）条件（C），如果对任意固定和ε＞0，存在和E的有限维子空间Em，使得

其中dimEm＝m和Pm∶E→Em是一有界投影，记B（E）是E的所有有界子集的集合.

i）T（r）∑＝∑，∀r∈R；

定理1[8]在假设I下，过程族，σ∈∑有紧一致（关于σ∈∑）吸引子，它满足，如果它有

i）一致有界吸收集B0；

ii）满足一致条件（C）.而且，如果E是一致凸的Banach空间，则逆也成立.

引理1[9]如果，则对，则下面的结论成立

定理2[6]（E0中有界一致吸收集的存在性）假设（F1）—（F3）成立，如果，则（1）式在E0中有一致吸收集.即就是，存在μ0＞0，对任何有界集B⊂E0，存在，使得

为方便起见，我们引进符号E0＝V×H，E1＝D（A）×V.

2 E1中的一致吸引子

2.1 E1中的一致有界吸收集

定理3假设（F1）—（F3）成立，如果，则（1）式在E1中有一致吸收集.即就是，存在μ2＞0，对任何有界集B⊂E1，存在，使得

用Av＝Aut＋εAu乘以（1）式在H中作内积

由（4）式，定理2，Hölder不等式及Young不等式，得

根据（F2），定理2和Sobolev嵌入定理，有g（u），g′（u）在L∞上一致有界的，即就是，存在常数K3＞0，使得

结合（8）-（12），由（7）式得

由ε的任意小，取ε＞0足够小，使得

并令α－εγ＝δ，则由（13）式可得

根据（9）可得

即有

因此我们得到E1中的一致吸收集B1.证毕.

2.2 E1中的一致吸引子

引理2[10]设g∈C2（R，R）且满足（F2），则g∶D（A）→V是紧连续的.

其中B1是E1中的一致（关于h∈H（h0））吸收集.

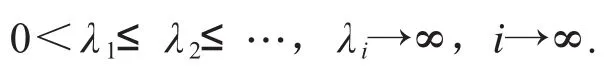
其中Qn∶D（A）→Gn都是正交投影，对任意的（u，ut）∈E1，作如下分解

取0＜σ0＜1，用Av2＝Au2t＋σAu2与方程（1）相乘，并在H中作内积可得

[1]BALL J M.Initial-boundary value problems for an extensible beam[J].J Math Appl，1973，42（1）：61-90.

[2]BALL J M.Stability theory for an extensible beam[J].J Differential Equations，1973，14（3）：339-418.

[3]王素萍，马巧珍，邵旭馗.梁方程的指数吸引子[J].西南大学学报（自然科学版），2011，33（9）：29-35.

[4]马巧珍，孙春友，钟承奎.非线性梁方程强全局吸引子的存在性[J].数学物理学报（A辑），2007，27（5）：941-948.

[5]陈小豹，马巧珍.非线性可拉伸梁方程强全局吸引子的存在性[J].西北师范大学学报（自然科学学报），2008，44（6）：1-6.

[6]李志宇，马巧珍.非线性可拉伸梁方程的一致吸引子[J].西南师范大学学报（自然科学版），2012，37（4）：34-38.

[7]CHEPYZHOV V V，VISHIK M I.Attractors for equations of mathematical physics[M].Providence RI：Colloquium Publications American Mathematical Society，2002.

[8]ZHONG C，WU H，LU S，et al.Atrractors for non-autonomous 2d navier-stokes equations with normal external forces[J].Discrete Contin Dyn Syst，2005，13（3）：701-709.

[9]MAS，ZHONGCK.The attractors for weaklydamped non-autonomous hyperbolic equations with a newclass of external forces[J].Discrete Contin Dyn Syst，2007，18（1）：53-70.

[10]MAQZ，ZHONGCK.Existence ofstrongsolutions and global attractors for the suspension bridge equations [J].Nonlinear Anal，2007，67（2）：442-454.

[11]MAQZ，WANGSP，CHENXB.Uniformcompact attractors for the coupled suspension bridge equations[J]. Appl Math Comput，2011，217（14）：6604-6615.

[12]马巧珍，钟承奎.吊桥方程全局吸引子的存在性[J].四川大学学报（自然科学版），2006，42（2）：271-276.

[13]ROBINSONJ C.Infinite-dimensional dynamical systems.An introduction todissipative parabolic PDEs and the theory of global attractors[M].Oxford：Cambridge University Press，2001.

Existence of Uniform Compact Attractors for the Tension Beam Equation

WANG Suping，SHAO Xukui
（School of Mathematical and Statistics,LongdongUniversity,Qingyang745000,Gansu,China）

When forcing term h only satisfies condition（C*）,the existence of uniform compact attractors for the non-autonomous extensible beam equations is proved in a strong topology space E1＝D（A）×V by using the uniform condition（C）.

extensible beam equations;uniform condition（C）;condition（C*）;uniform attractors.

O175.15

A

1001-4217（2016）04-0057-07

2015-12-17

王素萍（1981—），女，甘肃庆阳人，副教授.研究方向：无穷维动力系统及偏微分方程的研究. E-mail：shwangsp@163.com

国家自然科学基金资助项目（11161402）；甘肃省高等学校科研项目（2015A-147）；陇东学院青年科技创新项目（XYZK1401）．