三角形几何量的秩序图和量级图初探

刘保乾

（西藏自治区组织编制信息管理中心，西藏拉萨850000）

三角形几何量的秩序图和量级图初探

刘保乾

（西藏自治区组织编制信息管理中心，西藏拉萨850000）

以不等式自动发现与判定程序agl2010为工具，通过对已知不等式进行隔离研究，提出了研究三角形几何不等式的有向图表示方法，并绘制了三角形中部分几何量的秩序图和量级图；讨论了秩序图和量级图的数据描述结构；隔离了一些著名不等式结果；提出了待解决的不等式问题.

有向图；三角形几何不等式；不等式自动发现；量级

0 引言

三角形几何不等式数目繁多，内容丰富，特别是由于机器证明软件的出现（如DISCOVERER程序[1]，Bottema软件[2]和agl2010程序[3]等），使这类不等式的发现呈现出井喷的态势.如何理出这些大量的、形式各异的不等式之间的关系和秩序，进而剖析其规律，是一个十分有价值的工作.本文以不等式自动发现与判定程序agl2010为工具，通过对ΔABC中的不等式

进行隔离研究，在对众多隔离结果进行分析和研究的基础上，提出了用有向图研究三角形几何量之间关系的一种思路和方法，为数量研究三角形提供了新的视角和课题.

以下约定ΔABC三边上的中线为ma，mb，mc，高为ha，hb，hc，角平分线为wa，wb，wc，旁切圆半径为ra，rb，rc，类似中线为ka，kb，kc，内切圆半径为r，外接圆半径为R，半周为s.用表示循环和.

1 过滤等价式

要用agl2010程序得到不等式的隔离式，首先要构造数据集，数据集中元素的数目及元素的形式将影响分隔结果的多少及形式.为了得到较为精确的隔离式和提高运算效率，需要过滤掉数据集中的冗余元素.文献[4]曾编写过一个等价式过滤程序，但由于程序功能比较简单，难以处理形式复杂的三角形表达式.为此需要探讨新的算法.

过滤等价式，从本质上讲是判断两个表达式是否恒等.在agl2010程序中，判断两个非根式型几何量表达式相等的方法是，先将表达式代数化，再进行比较，具体命令是：

如果执行的结果是零，则表示ex1＝ex2是恒等式.对一些根式型几何量（如角平分线wa，半角三角函数等），则要将其化为等价的锐角三角形表达式，然后再代数化，具体命令是factor（aptoxp（subs（lsta，ex1－ex2）））.但这种方法最大的缺点是判定过程容易出错，且效率不高.为了建立对任何表达式都适用的通用算法，可用赋值验证的方法，即对两个表达式赋若干组数值（本文取了3组数据），如果用这些数值能够验证两个表达式相等，则暂且认为它们是恒等的，这样就可以通过程序将等价式初选出来，最后再对搜索出来的恒等式进行验证确认，以得到正确的结论.具体通过如下程序csxd来实现：其中语句2排除了分母为零的情况，语句3分别测试了三组数据[2，3，4]，和[11，473，5001]，如果测试通过，则返回1，否则返回－1.

调用csxd模块就可以编写过滤等价式程序trghds.程序trghds对一个数据集ex中的等价式进行过滤，并打印出过滤过程中产生的副产品——恒等式；程序的返回值是一个过滤掉等价式的数据集.

例1在ΔABC中，构造一个零次对称数据集，并过滤掉其中的等价式.

解键入命令：

经测试知，数据集ls中共有165个元素，这些元素中已经没有冗余数据.为了输出发现的恒等式，可键入指令bf：＝glpfhds（hd），最后在bf变量中得到77个较有意义的三角形恒等式，如

2 不等式（1）的隔离与几何量的秩序图

agl2010程序有现成的隔离不等式命令，具体地说，隔离不等式M≥N的命令是：

其中d是参与隔离的数据集；bz表示何种类型的不等式，bz＝0表示3元代数不等式或者三角形几何不等式；xs表示隔离结果是否实时显示，xs＝1表示显示.程序trg_fgs的功能是对不等式M≥N进行隔离，返回值是一个数据集{qi}，并且有不等式链M≥qi≥N，称qi为不等链的节点.为了减少数据量，现取ΔABC中最基本的元素a，ha，ra，ma，wa，R，r，s和三内角的正弦、余弦，进行简单的求和与求商运算构造数据.具体命令如下：

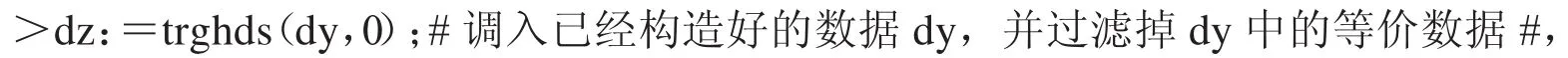
这样就得到了数据集dz.为了隔离不等式（1），运行如下命令：

这表示已经开始在数据集dz中搜索不等式（1）的隔离式.经过148.762 s运算后，输出隔离式集，现选其中若干优美的几何量，构成集合df＝{qi}，qi的具体表达式如下（限于篇幅，有些表达式这里没有给出）：

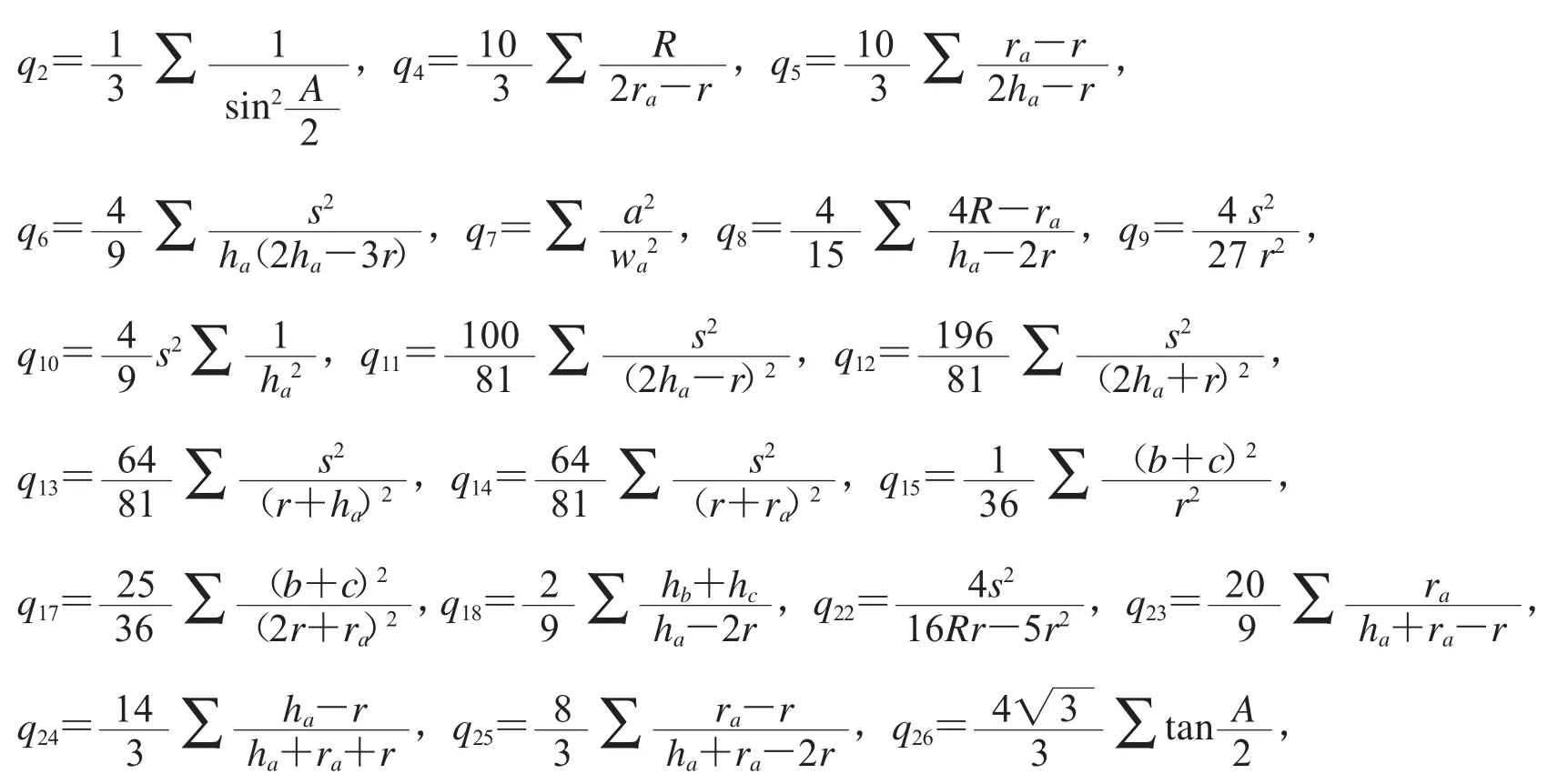
注意这些不等式之间的关系是平行的，还没有构成不等式链.为了进一步隔离不等式（1），下面对各节点再进行隔离.键入命令：

则输出集合{q6}，这说明有不等式链q1≥q6≥q2.接着键入命令：

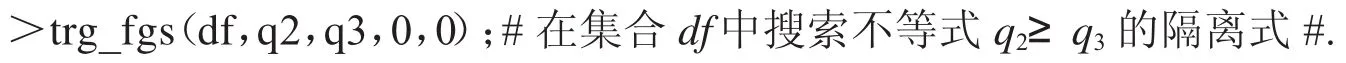
则输出集合{q8，q16，q19}，这说明有不等式链

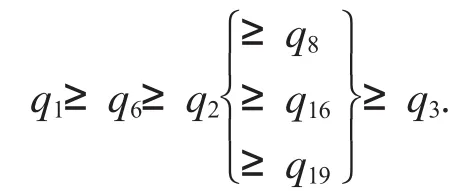
为了确认q8，q16，q19之间的大小关系，现用不等式自动发现与判定程序agl2010的随机数验证程序otf直接进行测试（返回值是1表示表达式是非负的），这样就可以进一步得到不等式链q1≥q6≥q2≥q19≥q8≥q16≥q3≥q0.键入命令：

则输出集合{q2，q11，q17，q19}，这说明有不等式链

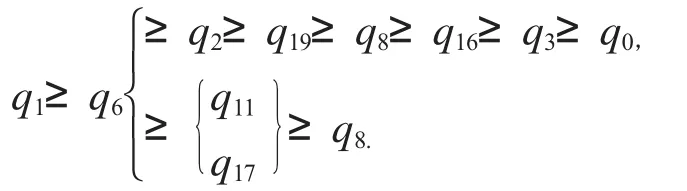
用otf程序测试q11和q17之间的大小关系，上不等式链可修改为

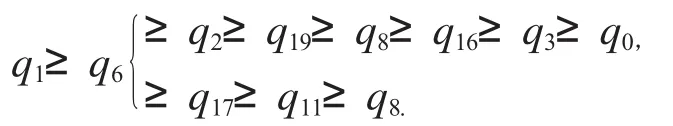
这样就可以用程序trg_fgs和随机数验证程序otf交替使用的方法得到隔离式.但随着分隔链的加长，节点数目会越来越多，这样用不等式链表示会遇到困难.为了解决这个问题，下面用有向图来描述不等式链之间的关系（有向图等概念请参阅文献[5]）：图中的每个顶点对应一个几何量，有向图的边代表几何量的大小关系.如不等式M≥N可表示为M→N，这样就可以把不等式链中的诸节点连起来.如果两个表达式大小关系不确定，则不产生边.按这些原则，上不等式链就表示为图1.

图1

由于这个有向图直观地反映了各个分隔点中几何量的位置关系和顺序，故称此图为几何量的秩序图.由于qi的次数是零次的，故也称此图为几何量的零次秩序图.分隔不等式（1）的一个较完整的零次秩序图见图2（为了标识方便，用ID号i直接表示qi）.

图2

秩序图直观地反映了一个不等式与其它不等式的强弱关系.在秩序图中，从某顶点开始沿着有向边的方向出发，到达另一个顶点所经过的路程称为由该点到另一个顶点的路径，开始的点称为路径的始点，终止的点称为路径的终点；每个边中箭头所指的顶点所代表的不等式强于箭头发出者的那个顶点，即每一个路径都代表一个不等式链；如果顶点之间没有边连接，则表示这些顶点之间构成的不等式不分强弱.找出一个图2中的最长路径（即包含的边数最多）很有趣.

另外，在秩序图中顶点之间的连接情况各异，一些顶点可能与多个顶点相连，而一些顶点则比较特殊.如果一个顶点只有后继点而没有前驱点，则称该点为左孤立点，在图2中，q1就是一个左孤立点.如果一个顶点只有前驱点而没有后继点，则称该点为右孤立点；在图2中，q0就是一个右孤立点.如果一个点没有边与秩序图中的任何一个顶点连接，则称该点为秩序图的孤立点.随着秩序图上顶点（几何量）的增加，一些孤立点可能会转化为非孤立点，并且产生新的孤立点.

如果不等式M≥N一旦确定，则几何量M和N可看作是一个参照系中的两个参考点，以这两个参考点作比对，其它同量纲的几何量总可以找到自己在参照系中的位置.这也可看作是对秩序图的一种直观解释.

解由于有不等式q57≤4，故q57和q0之间边的方向是从q0指向q57（此时q0由右孤立点转化为非孤立点）.为了在秩序图上反映出这类几何量，可考虑对更弱的不等式

进行隔离，就是说秩序图是完全开放的.

例3在图2中，有路径30→22→25→24→23→37→0（注意图2中有些顶点未标出），这说明有不等式链q30≥q22≥q25≥q24≥q23≥q37≥4，具体的不等式链是

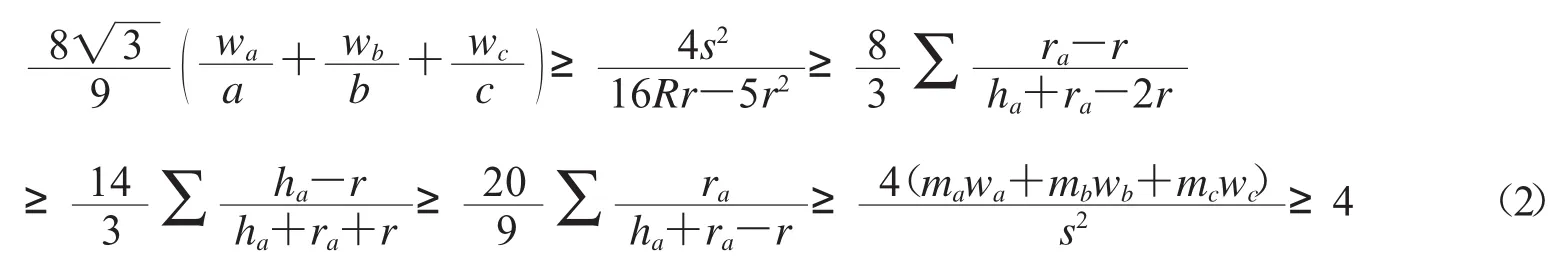
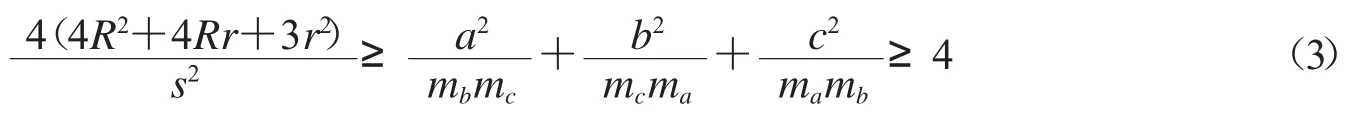
不等式链（3）隔离了Gerretsen不等式4R2＋4Rr＋3r2≥s2，十分优美.

类似可得到O·Kooi不等式R（4R＋r）2≥2s2（2R－r）的隔离式

3 量级图

如果把秩序图中的几何量qi按量级[6]大小进行分类，对分类后的量级进行有向图表示，则可以对秩序图进行简化，具体是：图中的各个顶点对应一个量级，有向图的边代表量级的大小关系，从而得到量级图.

为了对秩序图上的几何量qi进行量级分类，键入命令：

执行上述语句后按量级大小将qi分成12个子集，每个子集中的元素是几何量的ID号.具体情况是：

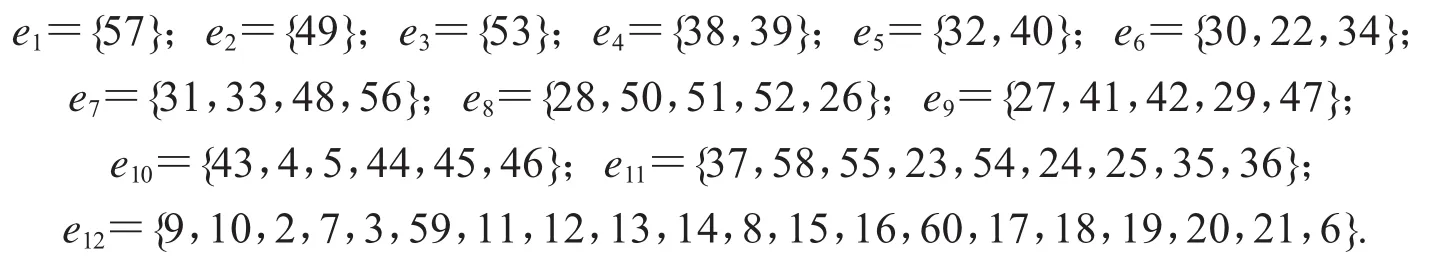
这些量级用R，r，s表示的参照式是（具体量级推导过程此略）：

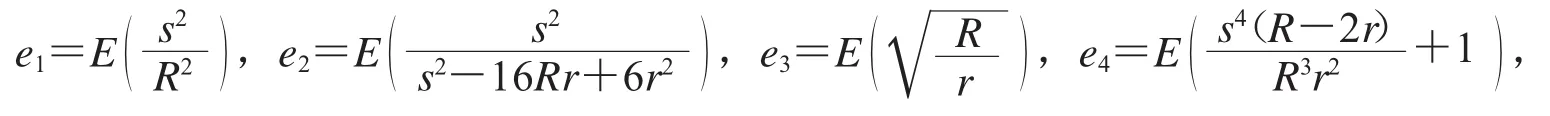
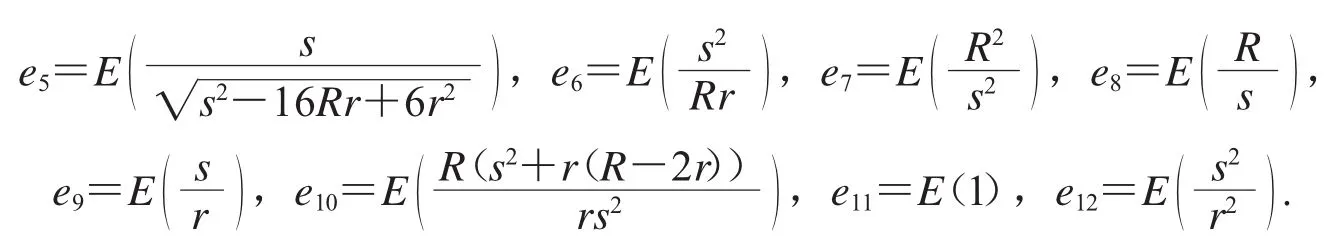
这些量级可用有向图3表示如下（为了简便，用ID号i表示ei）：

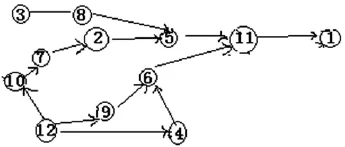
图3

由于这个有向图直观地反映了各顶点中量级的位置关系和大小顺序，故称此图为几何量的量级图.由于ei的次数是零次的，故也称此图为几何量的零次量级图.在量级图中，e12和e3的入度为零，是这个量级图中的最大量级；e1的出度为零，是这个量级图中的最小量级.

4 几何量秩序图和量级图的数据描述

当有向图中的顶点（几何量）很多时，要画出图就很复杂甚至不可能，即使画出来也会很凌乱（如图2中有些顶点虽未标出，但已经足够复杂），为此就需要用数据的方法对图形进行描述，这样做不仅解决了庞大图形的表示问题，而且可以为进一步研究奠定基础.

要确定一个顶点在有向图P0上的位置，只需要描述出该顶点的前驱点和后继点即可.如果某顶点qi∈P0，则可用一个列表数据描述其位置，这个列表数据是[{lj}，{rt}]，其中{lj}表示顶点qi的前驱点集，{rt}表示qi的后继点集，称列表[{lj}，{rt}]为qi在P0图上的坐标数据（也可简称为坐标），可记为qi（{lj}，{rt}）.由于有向图中的每个顶点可用其ID号标识，故qi点的坐标也可写成qi（{j}，{t}）的形式.有向图上所有顶点的坐标数据和ID号构成有向图的数据集，具体格式是{[i，{j}，{t}]}，即数据集中的每个元素是一个列表，每个列表由顶点的ID号和坐标构成.给定一个数据集，就可以绘出一张惟一的有向图；同样，从一张有向图也可得到一个惟一的数据集，即有向图和它的数据集是一一对应的，或者说是等价的.一个有向图既可以由一个具体绘出的图形表示，也可用一个数据集表示出来.

例4图2的数据集如下：

由这个数据集可知，q1为左孤立点，q0为右孤立点.

例5一个有向图S的数据集如下：

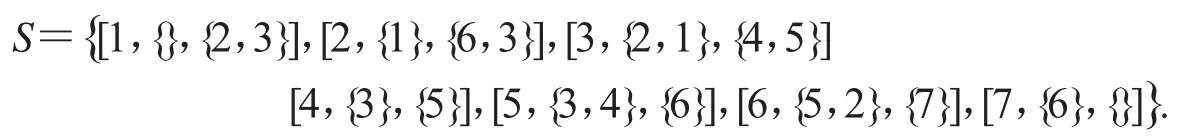
试画出S的有向图.

解根据题目中给出的数据集，画出S的有向图，得到图4，在路径3→4→5中，由于顶点3和顶点5直接相连，故是冗余边，应删除.同理知1→3边也是冗余的.删掉冗余边，最后得到图5.

图4

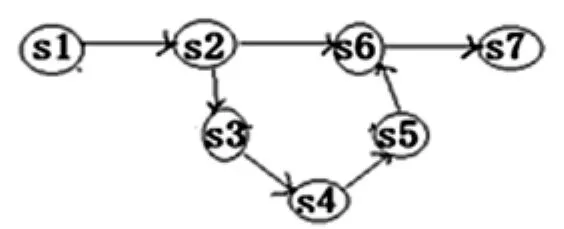
图5

例5说明，在一个有向图中，如果某个路径中的两个节点直接相连，则必是冗余的.利用这个结论可以快速绘出有向图.

前驱点集和后继点集中的几何量之间必不可分大小，利用这个特点可以查找有向图中的错误.程序crdbfdx可以判定一个集合中的元素之间是否不分大小，如果是，则返回1，否则返回－1，同时打印出能够分大小的几何量的ID号.调用crdbfdx，可以编写对一个有向图数据集进行查错的程序ddpas.事实上，图2就是借助于程序ddpas化简得到的.crdbfdx的源程序如下：

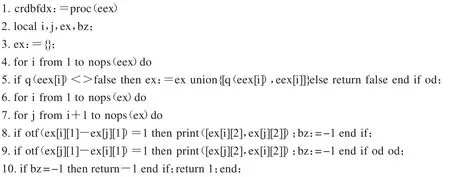
程序crdbfdx的输入参数是一个集合，集合的元素是顶点的ID号.语句5通过命令q将ID号转化为顶点所代表的几何量，并置入集合变量ex中，ex中元素的数据格式是[几何量表达式，ID号].语句8和语句9测试表达式正性，并设置返回标志，如果表达式为正，则打印出ID号.

例6查找如下图6中的错误（约定顶点上几何量的含义同于图2）：

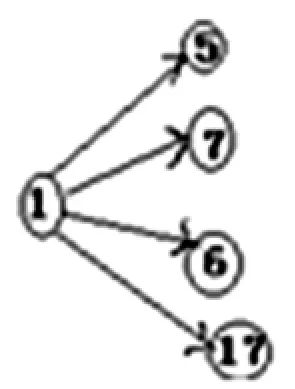
图6

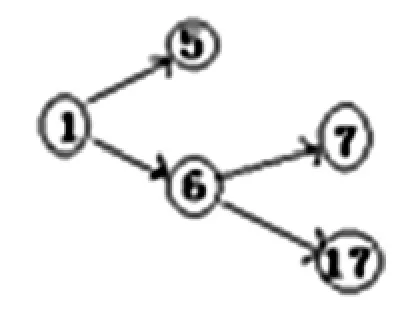
图7

解在图6中，q1有后继点集{5，6，7，17}，键入命令

输出-1，同时打印出[6，7]和[6，17]两个数据，这说明图6中有错，且提示可能存在路径6→7和路径6→17.用随机数验证程序otf测试知，图6可修改为图7.

解先将q62以数据集约定的格式录入秩序图的数据集变量中，即按[几何量，ID号]的格式录入.接着链入命令

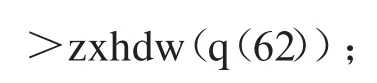
则显示3组数据

其中xy的含义是所有大于q62的几何量的ID号集合.找出xy集中每个元素在图2中可能存在的所有路径，每个路径的终点所构成的集合，即{29，27}形成q62的前驱点集.

dy的含义是所有小于q62的几何量的ID号集合.找出dy集中每个元素在图2中可能存在的所有路径，每个路径的始点所构成的集合，即{24，35}形成q62的后继点集.由此得到q62在图2中的坐标（bf的含义是一些与q62大小不确定的几何量的ID号集合）.

例7其实提供了在秩序图上增加顶点的一种方法，但要把这种方法转化为实际算法，还有许多工作要做.

5 结语

文献[6]曾指出，数量研究三角形的任务就是找出几何量的量级归宿，最终完善量级图.由本文可知，除量级图外，三角形几何量的大小关系秩序图也很重要，这两种图形整肃了三角形几何量的秩序，以直观生动的形式呈现了三角形几何量的一些特征和面貌，所以量级图和秩序图（简称为两图）构成了数量研究三角形的基础图形.任何一个已知的或未知的三角形几何不等式，都可在“两图”上找到自己的位置；有了“两图”，我们不仅可以认知单个孤立的几何量或不等式，而且还可以了解它左右邻旁的信息.树立这种观念是有益的，这不仅提高了发现不等式的主动性和效率，而且还可以指导我们径直走向目标.在“两图”的背景下，如果某个研究对象一旦出现，很快就会被一连串的关系式锁定.所以进一步研究和完善“两图”是十分重要的.最后再提2个问题：

问题1本文是用手工测试结合程序帮助的办法得到“两图的”.如何用图论的理论和算法研究“两图”，并用程序自动生成“两图”？

问题2给定一个有向图S的数据集，如何插入一个新的顶点，使插入新顶点后数据集自动更新？又如何输出S的一个最大路径？

[1]杨路，侯晓荣，夏壁灿.自动发现不等式型定理的一个完备算法[J].中国科学（E辑），2001，3（3）：273-288.

[2]杨路，夏壁灿.不等式机器证明与自动发现[M].北京：科学技术出版社，2008：117-142.

[3]刘保乾.不等式的自动发现原理及其实现[J].汕头大学学报（自然科学版），2011，26（2）：3-11.

[4]刘保乾.磨光集及其应用[J].汕头大学学报（自然科学版），2015，30（2）：44-55.

[5]方世昌.离散数学[M].3版.西安：西安电子科技大学出版社，2009.

[6]刘保乾.用对称性和量级研究三角形中的非负对称量[C]//杨学枝.不等式研究（第1辑）.拉萨：西藏人民出版社，2000：200-222.

Prelim inary Study of Order and M agnitude Graph of Triangle Geometrics

LIU Baoqian
（Information Management Center,Department of Organizational Information,Lasa 850000,Xizang Autonomous District,China）

The representation of directional graph of triangle geometrics is proposed for triangular geometric inequalities.It is achieved by separate examinations of known inequalities based on the program of Ag12010 for automatically finding and determining of inequalities.The data representation structures of order and magnitude graphs are s tudied.Several known inequalities are separated and open questions are also raised.

directional graph;triangle inequalities;automatically finding of inequalities; magnitude

O 122.3

A

1001-4217（2016）04-0030-10

2015-10-24

刘保乾（1962—），男，陕西凤翔人.E-mail：wshr987@163.com.