因势利导 顺其自然——以余弦定理的一个教学片断为例

赵娴静

(江苏省南京师范大学附属中学， 210003)

因势利导 顺其自然
——以余弦定理的一个教学片断为例

赵娴静

(江苏省南京师范大学附属中学， 210003)

学生对数学概念课常常有枯燥和索然无味的感觉．用什么方式进行概念课教学成为很多教师研究的课题，对此，笔者也进行了一些探索和研究.根据多年来的教学实践，笔者认为，概念课教学不管是问题情境式,还是学生探究式,这些方式都离不开以学生为主体．在解决问题时将学生的思维引入课堂,允许学生用他们自己的思路和关心的对象来解决问题,才能将“数学探究”在概念课中体现出来．

本文以余弦定理第一课时教学的一个片断为例,谈谈对“因势利导,顺其自然”教学方法的理解和反思．

一、教学片断

从这章标题“解三角形”入手,解三角形就是已知三角形中的一些量,求其他量的过程．正弦定理的学习中,已知一条边和两个角,可以解出三角形．那么，知道哪些量,就能确定三角形呢?

生:已知两条边及其夹角,可以解出三角形．

师:为什么?

生:根据初中学过的“边角边”来判断的．

师:很好，还有吗?

生:已知三条边,也可以解三角形,因为初中学过的三条边相等,两个三角形全等．

师:那么今天,我们就先研究:已知两边及其夹角,如何解三角形的其他量．

问题 在∆ABC中,已知AC=b,BC=a,∠ACB=θ,求解三角形.

看到题目后,学生很快都拿起笔,动手算起来了．笔者让学生停下笔,先不着急做,而是想一想:一是解决这个问题,你打算用什么方法?二是你可以尝试用学过的哪些知识来帮助解决这个问题?

提出这两个问题,主要是很多学生解题前,缺少对问题的思考与分析.正如波利亚“怎样解题”的第一步,有的甚至都没有审清题目,就匆匆动笔．正如工匠制作之前,先看看有哪些材料,即题目的已知条件是什么;再看看有哪些工具,即有哪些相关知识点,定理能帮助解决该问题，这样，制定出相关的计划后,再动笔实施．

在笔者的启发下,学生很快有了以下想法:

生1:可以尝试“作高”．

师:怎么想到的?

生1:这样，就可以将斜三角形转化成直角三角形,而且这个方法在上节课推导正弦定理时,就用到过．

生2:可以用向量这个工具来解解看．

师:怎么想到的?

生2:向量是既有长度,又有方向的量,它正好可以反映三角形里的边和角．正弦定理的推导过程中,向量也是一种方法．

生3:可以用正弦定理试着做．

师:怎么想到的?

生3:上节课刚刚学过的,可以用它帮助解决．

生4:我想用“圆”来做做看．

师:怎么想到“圆”的?

生4:上节课,正弦定理就可以用外接圆来证明,那么今天这个问题是不是也可以尝试用“圆”来解决．

学生在不到三分钟内就想出了四种思路．应当说,前两条思路是课本中的常规解法,也是我备课时准备好的,在意料之中．而后两种想法,出乎意料!但仔细想来,一个是用新学过的知识解决,一个是用之前类似的方法尝试解决,都合乎情理．

在和学生充分地分析、考虑后,大家再动手尝试着解决问题．经过大约十分钟的时间,很多学生都解决了问题,其中思路1和2的解法,在这里就不赘述了．而提出思路3和4学生,也有了演算过程,过程如下:

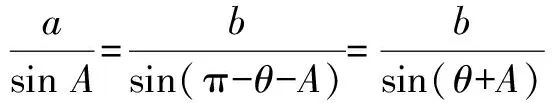
交叉相乘,展开得

asinθcosA+acosθsinA=bsinA，

所以 asinθcosA=(b-acosθ)sinA，

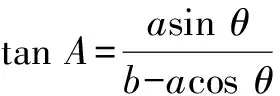
因为A∈(0,π),所以∠A唯一确定,进而求出∠B,

再由正弦定理,求出边c.

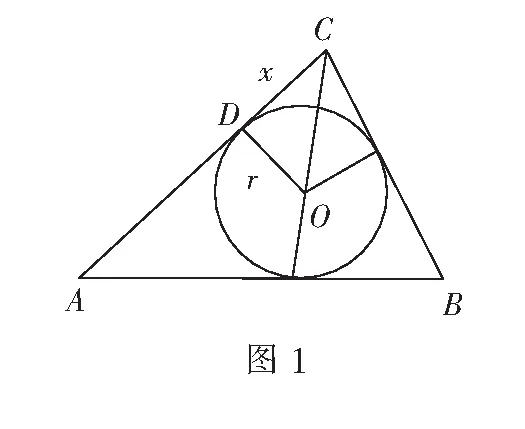
思路4 如图1,设∆ABC内切圆半径为r,CD=x,则有

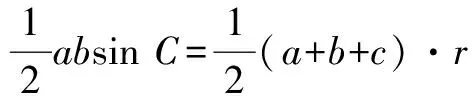
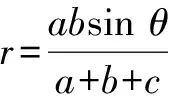
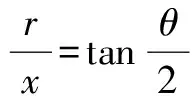
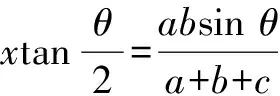
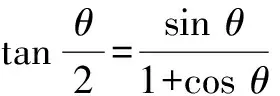
化简,得(a+b)2-c2=2ab(1+cosθ)，

即 c2=a2+b2-2abcosθ.

对于思路3,虽然没有直接推出这节课的“余弦定理”,似乎偏离了教学目的,但余弦定理的学习,不就是为“解三角形”而产生的吗?

对于提出思路4的学生,当他将演算展示出来时,大家都觉得新奇,在新奇的目光下,笔者将课堂交给学生,畅所欲言!

生5:我能看得懂,但想不到．

(下面有不少学生也有同感)

生6:刚才有同学提出的“圆”的方案,指的是外接圆,而怎么想到用内切圆来解决的呢?

生4:外接圆和内切圆都是三角形常用到的两种圆,我在尝试了外接圆,没有解决后,就试了试内切圆,而且刚学的面积公式,也和内切圆半径相关．

师:他不仅想法大胆,而且敢于尝试!这正是我们在今后各方面的学习、研究所需要的!

应当说,这也是新课程中探究式学习所需要的．

二、几点反思

1.关于教学设计

认知心理学家指出有意义的学习的三个重要条件(R.E.Mayer,1987)是接受、有效性和活动．当教师将学生的注意力集中在一个问题上,提供给他们一个所期望的场景或先行组织者时,接受和有效性条件相吻合(Glover&Corkill,1990)．通过模型化询问的过程和熟练解决问题的技巧,教师达到了活动的条件．当学生发展了探询和问题解决这两个方面的技能时,教师逐渐淡化帮助,让学生自己去承担越来越多的学习任务．

这节课的教学目的,是要推导出余弦定理.备课时，笔者上网查了许多“余弦定理”的教学案例,有以问题情境引入的,有告知学生定理内容,让学生证明的．考虑到目前测量工具的先进性,如果再用“挖隧道”,“凿山洞”等问题情境引入,显得与时代不同步，而直接让学生证明余弦定理,则缺少探究的过程．于是笔者借着上节课正弦定理,继续提供给他们一个解三角形的场景,让学生利用问题引导,来探索和发现余弦定理．

2.关于学生活动

这节课采用课堂教学常用的对话方式开始,鼓励学生调动他们自己的经验和已学知识与当前主题相联系,而不是通过呈现预先设计好的材料来促使学生对于学习任务的理解．很多时候,学生拿到数学问题,首先就是动笔做,多数人还没理清思路,甚至还没有看清题意,就着急动笔演算了,想一步,算一步,算了这步,不清楚接下来求什么．因此,学生的活动要有针对性,要有目的,这就需要教师为他们的自主活动搭建舞台,让他们在舞台上尽情展现．那些提出思路的学生应该算“先行的组织者”了，他们把这节课要解决的问题和现有的知识联系起来,从不同的角度,提出了合理的设想,为解决问题打下了基石．因此,教学中利用学生的思路,是获得重要概念、模式和抽象理论的手段．

其实，笔者的教学设计中并没有第三和第四种解法,而学生既然提出了这些既合情又合理的想法,为什么不试一试呢?于是借着学生的思路,把课堂交给了学生．

很庆幸,这节课学生提出的四种思路,都能解决该问题．其实,在很多时候,有些合情合理的想法,不一定能解决问题,这就需要教师在教学中适时地加以引导,以寻求合适的解决方法．