一题多解话审题

刘均锋

(广东省高州中学，525200)

一题多解话审题

刘均锋

(广东省高州中学，525200)

审题是为了正确解题而进行阅读、理解题目所涉及的数学知识,明确题目所给出的条件和要求,并试图找出条件和结论之间的关系而进行的思维活动．审题时要善于观察,多方联想、学会构造、合理转化,以发现知识的内在联系,从而寻找合理的解题途径．本文以一道三角题的研究性学习为例,窥探审题的奥秘．

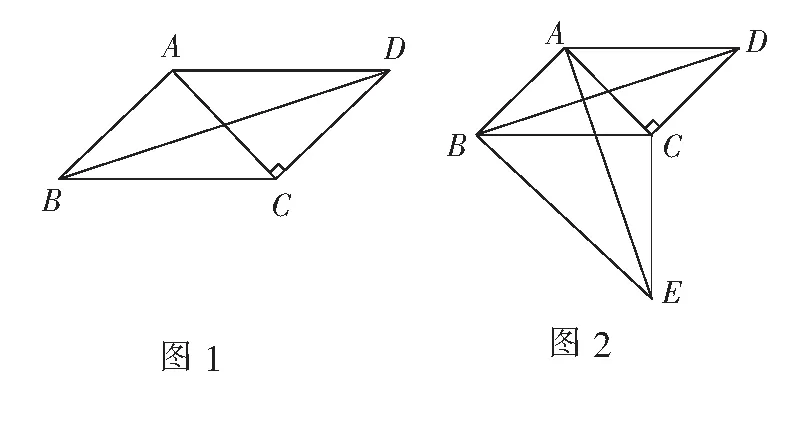
学生在分组合作探究研讨的基础上得出如下解法:

解法1 如图2,作CE⊥ BC,CE=BC，

则

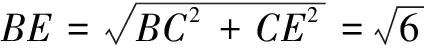
∠ACE=∠DCB.

又CE=BC,AC=CD,

∴∆BCD≌∆ECA,

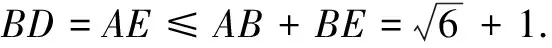
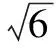
评注 条件是解题的主要材料，充分利用条件间的内在联系是解题的必由之路．审视条件要充分挖掘每一个条件的内涵和隐含的信息，发挥隐含条件的解题功能．本解法依据初中知识构造全等三角形,把BD转化为∆ABE的边AE,再据三角不等式求得BD最大值．这是在充分审视已知条件AC⊥CD,AC=CD的基础上引发联想产生的妙解．

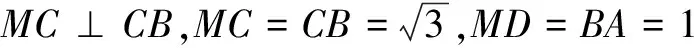
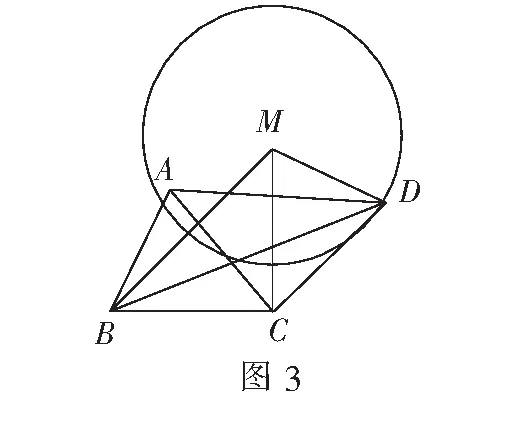
评注 结构是数学问题的搭配形式，某些问题已知数式结构中常常隐含着某种特殊的关系．审视结构要对结构进行分析、加工和转化以实现解题突破．本解法在审视图形结构基础上,把∆BAC 绕点C顺时针旋转90度到∆MCD位置,使AC与CD重合,得点D在以M为圆心,半径为1为的圆上,在∆BDM中用三角不等式求得BD最大值．联想的触发点依然是AC=CD, AC⊥CD这一已知条件．

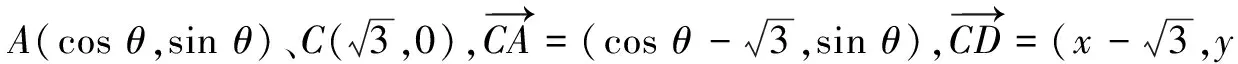
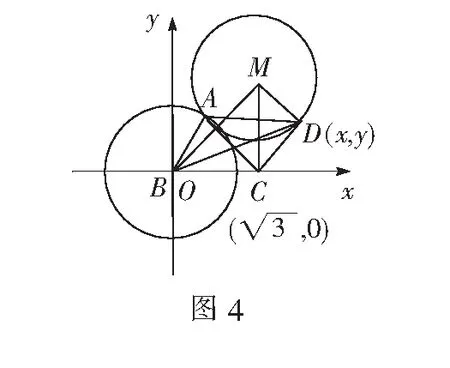
因为AC=CD, AC⊥CD,

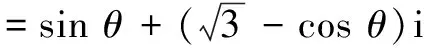
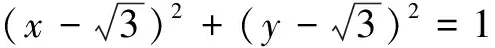
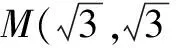
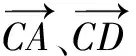
解法4 由平面几何的托勒密定理:四边形对角线的乘积小于或等于两组对边的乘积之和,当且仅当四点共圆时取等号，可得

AC·BD≤AB·CD+BC·AD.

记AC=CD=m, 则

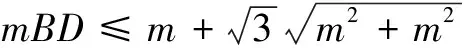
当且仅当A、B、C、D四点共圆时等号成立．

评注 结论是解题的最终目标，解决问题的思维很多情形下都是在目标意识下启动和定向的．审视结论要探索已知条件和结论间的联系与转化规律，善于从结论中捕捉解题信息，确定解题方向．本解法在学生自学平面几何的托勒密定理基础上,审视已知条件与结论,对号入座,直接运用定理快速得出结果．

解法5 参照图1, 记∠ACB=α,∠ABC=θ.

∆ABC中,由正弦定理，得

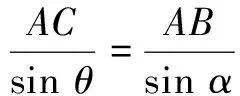
∴ACsin α=ABsin θ=sin θ.

∆BCD中,由余弦定理，得

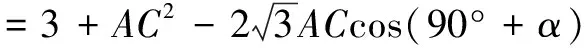
评注 范围是对数学概念、公式、定理中涉及的一些量以及相关解析式的限制条件，审视范围要适时利用相关量的约束范围从整体上把握问题的解决方向．本解法充分挖掘题中已知条件,在∆ABC、∆BCD中分别运用正弦定理、余弦定理产生边与角的联系,把问题转化为求三角函数的最值问题,一环扣一环,水到渠成．

解法6 如图5、图6,记∠ABC=θ,θ∈(0°,180°).

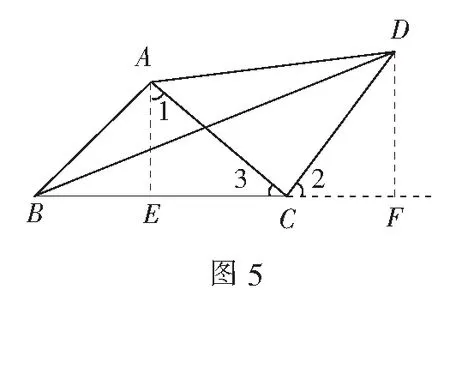
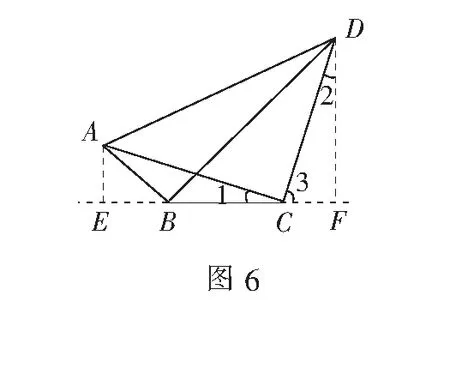
当0°≤θ≤90°时,作AE⊥BC于点E,作DF⊥BC于点F.

因为AC=CD, AC⊥CD,所以

∠1=∠2=90°-∠3,

所以Rt∆AEC≌Rt∆CFD.

从而有CF=AE=ABsin θ=sin θ,

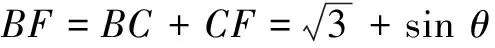
BE=ABcos θ=cos θ,

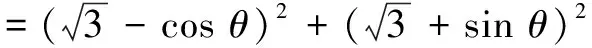
当90°<θ<180°时,同理可得

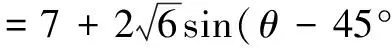
∴θ=1350时,

评注 形象是数学问题的几何形式，审视形象要把握形象的本质特征或赋予问题中的某些代数关系以几何意义,借助图象作出透彻分析，从而提供解题途径．本解法在充分审视已知图形形状基础上,大胆构造三角形全等,结合解三角形知识,厘清BD与∠ABC=θ的联系,把问题转化为求三角函数的最值问题,显得新颖别致．

从以上解法分析我们可以看到:审好题是解好题的重要一环．在一些复杂的数学问题里,有的条件往往不是那么醒目,而是以隐藏的形式存在．它们有知识性隐含条件(如解法1、解法2、解法3用到的三角不等式)、临界条件性隐含条件(如解法5、解法6中角θ的取值范围)、数据性隐含条件(如解法2、解法3中由MD=1、AB=1联想到单位圆)等．把隐含条件挖掘出来,常常是解题的关键所在．我们对题目隐含条件的挖掘,要从给出的条件出发,展开联想的翅膀,大胆构思,才能创造性地解题．

(本文为广东省教育科研“十二五”规划2012年度研究项目《“立体引学”模式在教学中的应用研究》,课题审批号2012YQJK219成果)