函数概念教学的若干思考

杨 梅

(江苏师范大学数学与统计学院,221116) (河南省商丘市夏邑实验中学,476000)

函数概念教学的若干思考

杨 梅

(江苏师范大学数学与统计学院,221116) (河南省商丘市夏邑实验中学,476000)

函数是现代数学的重要内容,也是世界各国中学数学课程的重要内容.函数的概念是高中数学的重要概念之一,同时也是学生进入高中阶段遇到的第一个难点,对函数概念的理解也将会影响学生对函数后续内容的学习和理解.因此,有必要探讨如何更好地优化函数概念的教学设计,促进学生对函数概念的本质理解.以下是笔者在构思教学设计时的一些思考.

一、对教学目标的思考

教学目标是教学设计的出发点,也是一切教学过程和教学活动的根本归宿，因此,在教学设计前,有必要厘清本节课的教学目标. 本节课是函数的第一节课,函数概念的抽象造成了其难懂、难学.因此,本节课应当通过大量丰富的实例展示函数概念的形成过程,帮助学生深刻理解函数概念的本质在于对应,引导学生在大量丰富的实例的支撑下用集合语言归纳函数的概念,并通过有效的例题帮助学生进一步加深对函数概念本质的理解. 因此,本节课的教学目标应定位于以下两点:

一是在大量丰富的函数实例的支持下,让学生经历函数概念的形成过程,并能用现代集合语言归纳函数的概念.

二是运用例题帮助学生进一步加深对函数概念的认识和函数概念本质的理解.

二、对教学过程的思考

纵观历史上函数概念的发展,众多数学家从集合、代数、对应、集合的角度不断赋予函数概念以新的内涵,从而推动了整个数学的发展. 函数概念的一次次提出、一次次推翻、一次次修正、一次次完善,是后人对前人思维的一次次突破. 因此,教师可以还原函数概念发生的历史过程,当然这里所说的历史过程应当是函数概念发生过程的课堂浓缩,而不是现实版的历史过程. 从函数概念发生、演变的历史过程中选取若干有代表性的观点并结合有关实例编织函数概念的发生、发展线路图. 如下表:

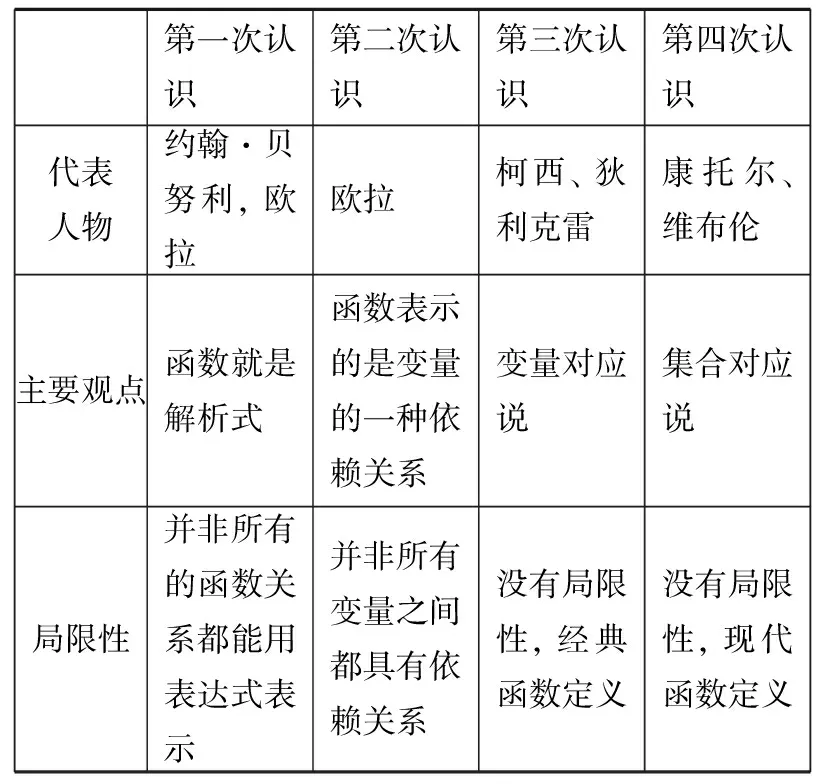
第一次认识第二次认识第三次认识第四次认识代表人物约翰·贝努利，欧拉欧拉柯西、狄利克雷康托尔、维布伦主要观点函数就是解析式函数表示的是变量的一种依赖关系变量对应说集合对应说局限性并非所有的函数关系都能用表达式表示并非所有变量之间都具有依赖关系没有局限性，经典函数定义没有局限性，现代函数定义

还原函数概念的发生、发展和形成过程,意图有两点:

其一,以学生的已有认知作为新知的重要生长点.所谓知识的生长点,是指“对学习新知识起支持作用的原有知识,或者能使所获得新知识被固定在认知结构中某一部位的那些知识.” 现代学习理论中的认知同化理论认为,数学学习主要是有意义的学习,如果原有认知结构中的某些观念能与新知识发生实质性的、非人为的联系,可根据新旧知识的逻辑关系,把原有的认知结构主动地与新知识相互作用,形成新的认知结构. 因此,在教学前,要充分了解和分析学生的原有认知结构中是否具有适当的能够与新知识建立联系的知识生长点,找到知识生长点有助于找到新知识的源头活水,才能使探求新知识成为可能. 学生初中阶段所学的“函数的变量对应说”(函数的经典定义)是新知识“函数的集合对应说”的知识生长点.

其二,渗透数学文化,引导学生体会数学的理性精神.函数概念的整个历史进程中,经历了无数数学家“一次次的提出概念、一次次的推翻概念”的探究过程,不断地引发更多的数学家在函数概念和函数本质问题上进行更深层次的思考. 这是必然现象,因为人类在探索自然规律的过程中必然有各种假设,虽然后来发现某些假设是错误的,但正是前人的失败才使后人的思考走上了正确的道路. 通过明晰数学概念的发生、发展的过程,可以引导学生体会数学的人文价值、应用价值和科学价值,开阔学生的视野,加强学生对数学的宏观认识和整体把握,领会数学学科独有的理性精神

三、对例题选取的思考

本课的目标在于引导学生建构函数的概念,并能对函数的概念及其本质有较为深刻的认识. 因此,本节课的例题选取应摒弃大量技巧性繁杂的求函数定义域和求值域问题,而要把精力稳稳地放在帮助学生对于函数概念及其本质的通透理解上. 在例题选取时,笔者认为应注意以下两点:

其一,既要呈现函数概念的正例,以突出概念的本质属性;也要呈现函数概念的反例,以消除函数概念非本质属性的干扰.

例1 判断下列对应是否为函数:

(2)x→y,这里y2=x,x∈N,y∈R；

(3)x→1,x∈R;

(4)x→y,这里y=x-1,x∈N*,y∈N*.

其中(1)(3)的对应是函数,符合函数概念的本质属性;而(2)(4)不符合函数概念的本质属性,对应都不是函数,通过正例和反例的双向作用,更有效地突出函数概念的本质属性.

其二,选取教材的习题作为进一步加强学生对函数概念本质理解的例题.

例2 已知集合A=R,B={-1,1},对应法则f如下:当x为有理数时,f(x)=-1;当x为无理数时,f(x)=1.该对应是从集合A到集合B的函数吗?

例3 已知集合A={1,2,3,4},B={1,3,5},试写出从A到B的两个函数.

例4 请写出3个不同的函数y=f(x)的解析式,满足f(1)=1,f(2)=4.

例5 已知一个函数的解析式为y=x2,它的值域为{1,4},这样的函数有多少个?试写出所有可能的函数.

例6 已知一个函数的解析式为y=x2,它的值域为[1,4],这样的函数有多少个?试写出其中两个函数.