例谈二阶导数几何意义的应用

李思聪

(江苏省无锡市辅仁高级中学，214123)

○解题研究○

例谈二阶导数几何意义的应用

李思聪

(江苏省无锡市辅仁高级中学，214123)

函数f(x)在x=a处的导数f ′(a),其几何意义为f(x)的图象在该点处切线的斜率,通常用来描述函数上升或者下降趋势,是高中数学研究的重要内容.而函数f(x)的二阶导数f ″(x)在课程标准教学要求中并未出现,但是如果能够了解函数二阶导数的几何意义,在数学解题中恰当地加以运用,往往可以起到事半功倍的作用.

下面试举几个例子来体现二阶导数的应用.

一、直接用于解答填空题,获取正确结果

例1 已知a为正的常数,若不等式

对一切非负实数x恒成立,则a的最大值为______.

解析 依题意,可将a分离出来,构造函数,利用所构造函数单调递增的性质求其最小值,即可求得a的最大值.但是此方法计算复杂,如果不能合理地运用换元的技巧,则很难得到正确结果.

但是如果从二阶导数的几何意义入手,利用图形,可以得到如下的解法:

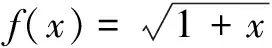
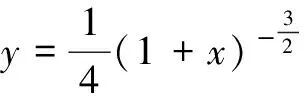
此例中,利用函数图象在x=0处函数值与导数值相等,根据函数图象上升的速度,得出不等式成立的充分条件是二阶导数f ″(x)>g″(x)；得到充分条件a≤8后,再检验必要性,从而得到a的最大值,不仅简化了计算过程,也是一个易于操作的解法.

二、提供解题的思考方向,简化解题的思维过程

函数凹凸性虽然不是高中数学的主要内容,但是教材中有相应的例题和习题,如果我们了解函数的凹凸性与函数二阶导数的关系,往往能对一些难以考虑的问题提供一个思考方向,在解题时简化思维的过程.

例2 已知函数f(x)=ln x-ax2-x,a∈R.

(1) 若函数y=f(x)在其定义域内是单调增函数,求a的取值范围;

(2) 设函数y=f(x)的图象被点P(2,f(2))分成的两部分为C1,C2(点P除外),该函数图象在点P处的切线为l,且C1,C2分别完全位于直线l的两侧,试求所有满足条件的a的值.

解析 第(1)问是基本问题,应用导数的方法容易解决.

第(2)问结合凹凸性思考可以得知,满足题意的点P,其必要条件是该点为函数凹凸性的分界点.由于二阶导数大于零函数下凸,二阶导数小于零函数上凸,因此点P满足题意的必要条件为函数在点P处二阶导数为零.

此例中,由题意根据图象可知函数在点P处二阶导数为零为满足题意的一个必要条件,但是由于这里的结论依赖图象,所以缺少必要的证明过程.在实际考试中,能得出答案甚至得分的同学寥寥无几,如果在解答过程中,从二阶导数,函数的凹凸性角度思考,不失为一个有益的尝试.

三、 探知压轴题的内涵,揭示压轴题的本质

有些压轴题,学生往往对题目背景比较陌生,做完之后还不能体会题目中蕴含的数学本质.

例3 已知数列{an}是首项为1,公差为d的等差数列,数列{bn}是首项为1,公比为q(q>1)的等比数列.

(1)若a5=b5,q=3,求数列{an·bn}的前n项和;

(2)若存在正整数k(k≥2),使得ak=bk.试比较an与bn的大小,并说明理由.

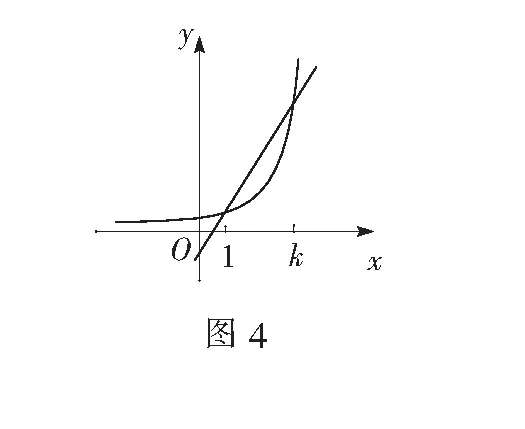
解析 第(2)问标准答案采取作差的方式,分类讨论得到结论,当1bn;当n>k时,an

如果从函数的角度考虑,可设an为一次函数f(x)图象上的点,bn为指数函数g(x)图象上的点.由于a1=b1,ak=bk且q>1,结合图形可知本题的结论被函数的凹凸性所决定.

由于g(x)为下凸函数,由图4可知:

当1bn;当n>k时,an

此题的本质,是函数凹凸性,学生往往对题目的本质没有把握好,或者缺乏一些思路而使得解答困难.如果我们在平时的教学中加入这些思路,可以拓展学生的思维,在数学教学中,知道一点永远比一无所知要好的多.

综上所述,在一些与导数有关的问题中,合理运用二阶导数的几何意义,有的可以为我们确知答案,有的可以给我们提供解题思路,有的还可以帮助我们探知题目内涵.在教学中,尤其是高三的复习教学中,可以进行适当训练,拓展学生的思维,让学生做到高屋建瓴,以达到一览众山小的境界.