求解无理函数值域的教学思考

☉江苏省西亭高级中学 马宇杰

求解无理函数值域的教学思考

☉江苏省西亭高级中学 马宇杰

函数是中学数学的一个重点，而函数值域（最值）的求解更是一个难点，能熟练掌握函数值域求法就显得十分的重要.笔者在高三的一轮复习中发现学生在求无理函数值域时只会做老师讲过的题目，题目略加变形学生就无从下手，针对这种情况，笔者进行了认真的反思：原来老师对这类例题的功能、本质没有完全把握.我们从几个例题来体会这类问题的实质及解决方法及今后在例题教学中如何发挥例题的功能，师生如何在挖掘例题的本质中提高学生的归类问题、分析问题、解决问题的思维能力.

方法一、整体换元

此类题将无理式整体换元，注意式子的结构和新变量的范围，否则将会发生错误.

点评：学生在解决本题时只记住了老师的解法（换元法），但不知为什么采用这种方法，更不知何时使用这种方法，所以解题思维、解题能力没有得到任何提高.本题应该这样教给学生入手：观察结构发现本函数的最高次是一次的，最低次是次，回想我们学过的函数中恰有一元二次函数中的次数呈现出二倍的关系，所以怎样转化为一元二次函数是首要解决的事情，所以通过换元达到了把次直接升幂的效果.此时学生学会了换元升

方法二、三角换元

观察无理式子内若含有一个常数减去一个变量的平方，则可以联想同角三角函数关系换元.

解：令x=cosα，α∈［0，π］，所以本题就转化为我们熟知的接着用辅助角公式就解决了.

点评：本题的实质都是一次的，故不要通过整体换元达到升幂的效果，观察根号中的结构（一个常数减去一个变量的平方）可以联想sin2α+cos2α=1.

方法三、配方法

若无理式下含有二次函数以及能通过换元法等转化为二次函数的题型可以用配方解决.

解：不妨设f（x）=-x2+4x（f（x）≥0），配方得

f（x）=-（x-2）2+4（x∈［0，4］），

利用二次函数的相关知识得f（x）∈［0，4］，

从而得出：y∈［-2，2］.

点评：在求解值域（最值）时，遇到分式、根式、对数式等类型时要注意函数本身定义域的限制，如本题的定义域要求为：f（x）≥0.

方法四、直接平方

方法五、有理化

若无理式直接平方不能使变量都集中在根号中，也无法通过以上的手段达到升幂的效果，此时就从函数的性质角度思考，对式子进行有理化.

方法六、利用几何意义

有的式子具有明显的几何意义，那可以考虑利用式子的几何意义解决，如可以转化为两点间距离.

解：本题可通过整体平方转化为一元二次方程在区间［0，2］上的有两解的情况，但是这个角度包含的运算太麻烦，从两点间的距离几何意义角度可以看成y=与y=kx+k的交点问题，而y2=1，且y≥0，表示以（1，0）为圆心以1为半径的上半圆，y=kx+k表示过定点（-1，0），故本题就转化为了过定点（-1，0）的直线与这个圆的上半圆有两个不同交点的问题.

方法七、利用数形结合

对无理式可以先换元，再根据数形结合的思想解决，下面结合几种形式展开介绍.

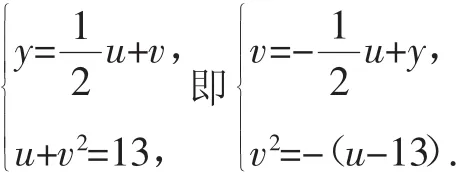
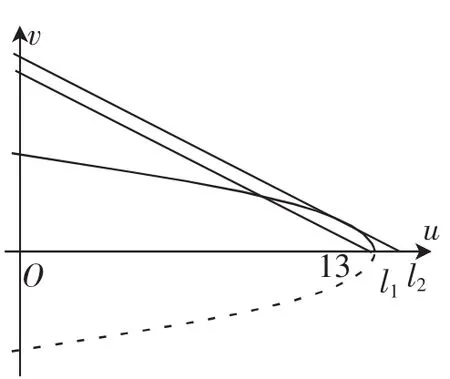
图1

如图1，显然，直线与抛物线相切时ymax=7，直线过（13，0）时

研究直线与抛物线相切及过某特殊点的直线就成了处理此类函数值域的一般性方法.

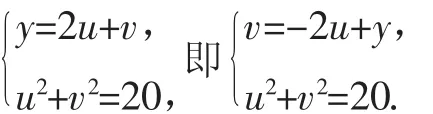
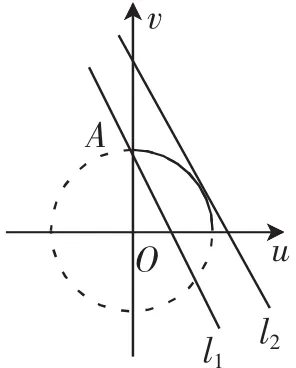
图2

所以ymax=10，过点的直线的纵截距显然为y的最小值.

图3中l1及l2两条直线所对应的y值为最大值和最小值.

2所以

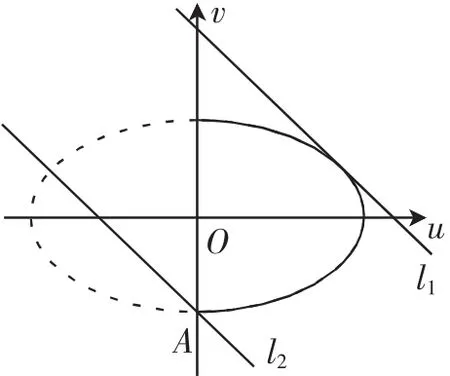
图3

现在求直线与椭圆相切时l1所对应的y2的值.由已知斜率的椭圆切线方程可知在v=-u-4+y中，所以

为促进规模化、标准化种植，提升农民的种植效率，日本政府提出生产资料购置补贴政策，鼓励农民按照相关标准进行种植生产。对规模化养殖、温室蔬菜种植，政府予以相关设施购买费用的补贴，其中由中央和地方财政补贴75%，剩余25%的费用可通过特定的金融机构进行贷款。2007年开始实施“跨品种经营稳定政策”，改革稻米生产调整及价格补贴，针对特定骨干农户，不分品种地对其整体经营收入进行补贴支持，加大对农地、水资源、环境保护等的政策支持。

则u、v同时满足

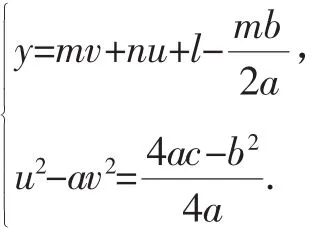
这时求函数值与问题转化为直线与曲线的位置关系问题，只需研究直线与曲线相切及过曲线某特殊点的直线即可.

方法八、构造向量

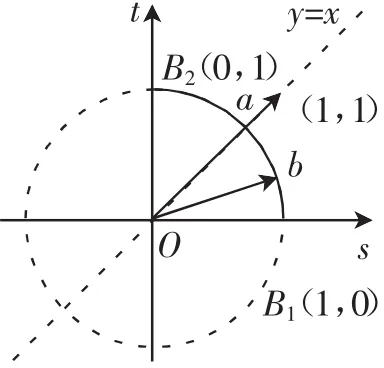
图4

点评：这类无理函数求值域的解题过程，实质上归结于简单的线性规划问题.约束条件：向量终点的集合，常向量是目标函数的法向量.与解析几何法的本质相通的.但相对而言，计算量比解析几何法求切线要小得多，学生出错的概率更小.

总之，解题教学不应重视一招一式，而应注重方法的自然性、普适性以及解题后的反思、提炼.讲一例题，学生记一个，学生在解决这类问题时仍然是不知从何下手，因此，解题教学中，教师的主要职能在于怎样帮助学生做好解题后的反思，充分挖掘例题本身的功能，做到“授之以渔”.对于无理函数的值域的求解，需要学生特别是在解题后进行分析、比较、反思、提炼，使这类例题的解题思维成为一种能力.