题不在多 启发思维则灵

☉西安交通大学苏州附属中学 单景丽

题不在多 启发思维则灵

☉西安交通大学苏州附属中学 单景丽

众所周知，数学教学离不开解题.但是近年来随着应试压力的加大，新课程标准提倡的让学生学会学习数学的教学更多成为一种理想状态，究其原因还是数学抽象、形式化的特点与学生认知、思维成长不能同步造成的.从初中数学到高中数学，数学知识的形式化程度一下提升了不少，诸如对于函数概念的界定抽象了不少，很多学生一直无法抓住函数概念更深层次的理解.

笔者认为，这也不能完全怪学生，造成这样的现状还是多方面的.因此，这也造成了教师用最直接粗暴的方式——题海训练对学生进行训练和巩固，只要训练各种各样的问题，势必对数学知识的运用起到一定的辐射效果，而且在短期内有很大的效果.这也是当下基础教育在理想和现实层面无法回避的矛盾.笔者也不敢否定这种训练的模式，至少其存在还是有一定的合理性.但从长期来看，这种方式势必对学生思维的培养有一定的阻碍作用，数学教学不能只做题而不思考、不能只训练而不总结，因此笔者认为在一定程度上需要做一些总结性的思考，特别是在有典型问题的解决上，要以“山不在高有仙则灵”的精神去引导教学，提高自身专业化水平的发展，发展学生的思维.

笔者认为，好的试题往往不止一个角度切入，这样的试题在追求知识运用的广度上有着非常全面的拓展，有助于学生通过一个数学问题的解答，获得更多知识整合运用的能力.这样的试题对于学生思维的启发往往是全面的、深刻的、多样的，值得教学深究和探索，这远比做一些杂乱无章的数学问题来的有效和更具思考.

例题 在平面直角坐标系中，A、B分别是x轴和y轴上的动点，若以AB为直径的圆C与直线2x+y-4=0相切，则圆C面积的最小值为____________.

分析：本题改编自2015年江西高考真题.该题是求圆的面积最小值，可转化为求半径的最小值.解决本题的关键就是找到圆的半径所满足的条件.通过分析题意可得到结论：圆心C到A、B、O三点的距离与到直线2x+y-4=0的距离都相等且都是半径.因此可以从不同视角去思考问题.

思维1：引导学生思考：为何到定点的距离等同于到定直线的距离？从这一条件入手是哪个基本知识点的运用？显然是抛物线的定义！因此问题这样思考：由已知得点C的轨迹为以O为焦点，直线2x+y-4=0为准线的抛物线，所以将问题转化为求抛物线上的点到焦点的距离的最小值.如图1，设原点O到直线2x+y-4= 0的距离为d，则点C到直线2x+y-4=0的距离是圆的半径r

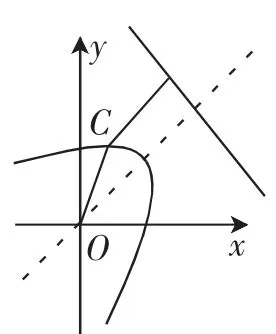
图1

思维2：考虑到抛物线并不在标准形态下，此时很多学生未必会使用思维1中的定义去思考，因此教师也可以利用第二种思维引导学生，即能否通过代数化的手段首先解决点C的轨迹问题？这应该是很多学生的第一想法，与学生共同探讨尝试.由已知得点C（x，y）的轨迹方程是化简整理得，曲线E：x2+4y2-4xy+ 16x+8y-16=0，将所求的问题转化为求曲线E上的一点到直线2x+y-4=0的距离最小值，此时只需将直线2x+y-4=0向曲线E平移，当与曲线E相切时，切点P（x0，y0）到直线2x+y-4=0的距离就是半径r的最小值.如图2，设切线方程为2x+ y+t=0，由消去y0得由于相切，所以Δ=（20t）2-4×25×（4t2-8t-16） =0，解得t=-2，此时，从而得到等式r=min

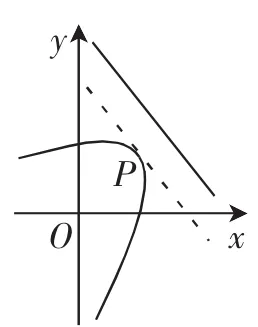
图2

思维3：圆是解析几何中最简单的二次曲线，相比椭圆、双曲线、抛物线而言，圆中的很多问题都有独特的解决方式.教师教学中引导学生思考，圆中的很多问题并非是完全使用解析几何代数化运算的方式解决的，可以利用哪种更为有效的途径？学生的思维迅速向几何方式靠拢，显然从几何方式的角度去思考与圆相关的问题，往往来得更为有效.这里教师向学生渗透了解析几何中不同曲线的解决思路：圆中的问题更倾向于几何方式，椭圆等曲线的解决方式更倾向于代数化的途径，思维的转化从这里得到了巩固和提升.设圆C与直线2x+y-4=0相切于点P，则由已知得圆C过点A、B、O、P，且有CP垂直于直线2x+y-4=0，如图3，显然当O、C、P三点共线时圆C半径取最小值，此时点O到直线2x+y-4=0的距离是圆C的直径.

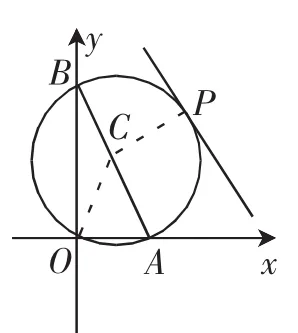
图3

思维4：圆是一种特殊的二元二次曲线，其不仅有充足的几何意义，也有非同一般的参数角度——三角函数.我们知道，圆方程的参数就是三角换元，利用圆的参数方程非常方便地解决与之相关的最值问题，这与三角函数求最值的简洁性密不可分.因此教师以三角函数设计代数化思维：设圆C的半径为r，点C的坐标为（rcosθ，（舍去）.

思维5：哥伦比亚大学教授张寿武先生说：“我的数学学习之路都是由运算铺成，我喜欢最质朴的想法，发自内心的道路，这时往往运算才是问题解决的关键.”笔者认为，很多学生能想到圆方程的一般形式，结合一般形式去思考、解决，运算势必成为最大的瓶颈.引导学生解决好圆的一般方程涉及的运算是关键：由已知可设圆C的方程为x2+y2+Dx+Ey=0，则联立方程组消去y整理得5x2-（2E-D+16）x+4E+16= 0，由已知得Δ=（2E-D+16）2-4×5（4E+16）=0（E≥-4），即所 以 圆 的 半 径r=由于t≥0，当时，r取最小值

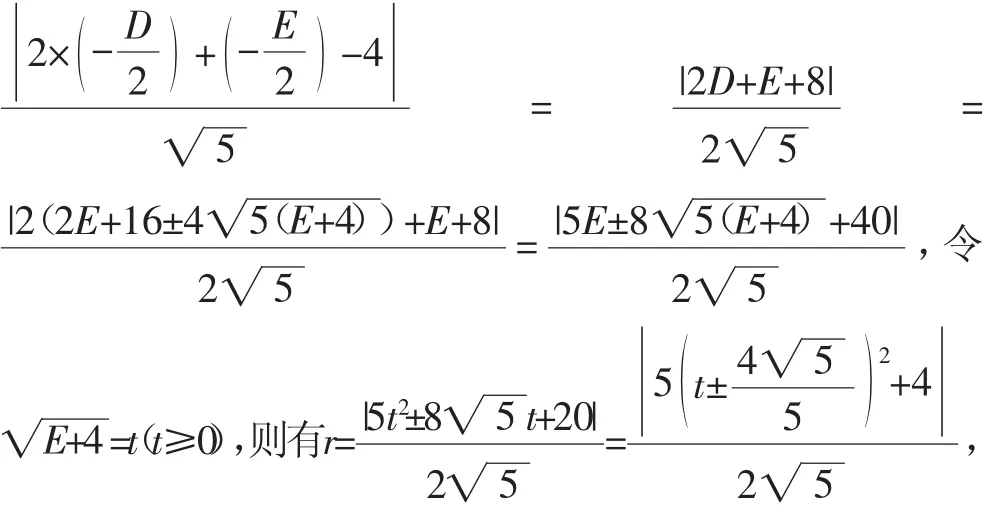
说明：解析几何中求最值的问题，已成为高考的热点和难点，其解题方法一般有两种解题思路：其一是几何法，即找出最值的几何意义，利用平面几何性质求解.最值的几何意义，常见的有：（1）最值的几何意义是求圆锥曲线上的点到焦点的距离的最值，其几何性质是顶点到焦点距离时取最值（比如解法1）；（2）最值的几何意义是求曲线上一点与直线距离的最小值，其几何性质是曲线上离直线最近的点到直线的距离取最小值（比如解法2）；（3）最值的几何意义是求有同一端点的两条线段之和（或差）的最值，其几何性质是三点共线时取最值（比如解法3）；其二是代数法，即找出所求的问题的函数关系表达式，把所求最值的问题转化为求函数的最值问题（比如解法4或解法5）.总之，对于解析几何中求最值的问题，一定要具体情况具体分析，不宜拘泥于代数法或几何法，宜灵活运用.从这一典型的问题中，我们不难启发学生所需要用的解决问题的基本思维和思想方法：

（1）思维的第一层次：做出问题解决方向的判断，一般从思想层面去思考，即代数方式解决还是几何含义下手，这是典型的思维起始之路.

（2）思维的第二层次：从思想层面入手思考的第二阶段即具体实施问题解决过程，代数的角度往往是运算倡导主导地位，其中所有问题都可以看成是某一变量x的函数，有时也能从特殊的自变量去尝试问题的解决（比如以角度为自变量的三角函数进行解决）；几何角度往往是图形化策略的思考，这里可以是一维状态下的几何意义，也可以是二维坐标系中的图像，都是几何方式最好的呈现，最典型的案例是求函数f（x）=|x-1|+|x+1|的最小值，既可以绝对值的几何含义下手，也可以从图像去思考解决.

（3）思维的第三层次：能从一种方式解决问题，还要学会从更多的角度去思考问题，这样思维才会有延伸性，若仅仅是解决问题、扔掉问题、不断重复，那么这样的学习过程依旧停留在浅显的表层，不具备深刻性，因此题不在多，具备启发思维则灵.因此，对典型问题的解决倡导进行多元化角度的思考，这远远比不断进行题海训练、不思考、不归纳来得高效和有深度.

1.付静.高三数学多变复习教学的有效策略［J］.中国数学教育，2014（9）.

2.鲍建生，等.浅谈数学问题串教学研究［J］.数学教学，2013（1）.