整体思想在高中数学解题中的应用

☉江苏省常熟市浒浦高级中学 胡 静

整体思想在高中数学解题中的应用

☉江苏省常熟市浒浦高级中学 胡 静

整体思想作为一种重要的数学思想，可以简化繁杂、抽象的数学问题，提高学生解决高中数学问题的能力，同时也可以使学生触类旁通、举一反三，使学生形成正确的解题思路.特别是随着新课标对高中数学教学提出了更高要求，提升学生解题能力刻不容缓.本文以整体思想为研究对象，着重探讨了其在高中数学解题中的具体运用，以期全面提升高中学生的数学解题能力.

一、树立整体意识，培养发散思维

在传统的高中数学解题训练的过程中，大多数数学教师都会为学生讲解多种形式的解题方法，尤其是教师会重点引导学生从局部到整体、从简单到复杂来简化数学解题过程，深化学生对于有关数学教学知识点的理解和认识，同时也有助于借助数学解题训练的过程中来巩固学生所掌握的解题技巧和能力.但是随着新时期教学改革进程的推进，传统的教学模式和解题思想已经无法满足现代化高中数学教学的需求，所以改变传统教学模式，引导学生逐步树立整体意识等整体思想解题观念，以为高中数学教学有效性的提升奠定扎实基础.但是为了确保学生可以灵活地运用整体思想来解决有关的高中数学问题，教师必须要先引导学生树立整体意识观念，培养学生的发散思维.比如，在讲解高中函数图像这部分数学知识的时候，教师需要先为学生讲解函数概念，接着再引导学生对函数图像的特征进行探索，以便使学生了解和掌握函数图像的对称性、周期性、奇偶性和单调性等基本函数特性.另外，在开展教学的过程中，教师也要加强整体思想等解题思想的培养，加快树立整体意识，以便帮助学生更好地解决有关的数学问题.

例1 已知某长方体六个表面面积总和为24，十二条棱的总长为24，求该长方体对角线的长度.

分析：如果在求出该长方体的三条棱长之后再求对角线的长度，那么实际的效率比较低，并且学生很容易在繁杂的计算过程中出现计算误差，不仅费时费力，实际的解题准确度也不理想.而此时如果学生可以在解题的过程中合理引入整体思想，那么就可以显著简化该问题的求解过程，下面就整体思想在该道例题中的具体应用进行分析.

解：假设该长方体的长、宽、高分别为a、b和c，那么由已知条件可得：2（ab+bc+ac）=24，4（a+b+c）=24，由此可求得：a+b+c=6，进而可得d2=a2+b2+c2=（a+b+c）2-2（ab+

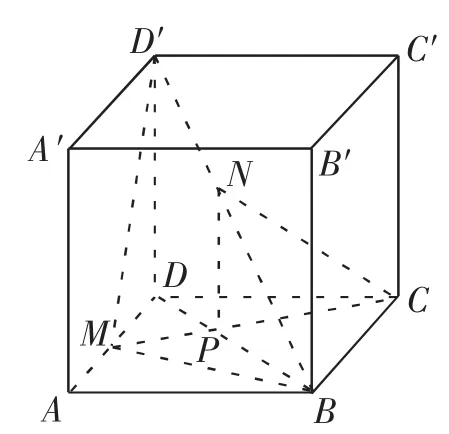
图1

例2 如图1所示，正方体ABCD-A′B′C′D′的边长为a，M是边长AD的中点，N是正方体边长BD′上某点，且已知边长BD和MC相交于P点，NB∶D′N= 2∶1.

（Ⅰ）证明：直线NP⊥平面ABCD；

（Ⅱ）求平面CC′DD′和平面PNC二者的夹角？

解析：针对该道例题的第一问，为了证明直线NP⊥平面ABCD，教师可以尝试引导学生证明直线NP⊥平面ABCD中的任意一条直线，可以为BD、CD和AB等，然后需要结合已知条件来逐步证明该结论，但是更为关键的是要引导学生可以从整体角度来入手，从繁杂的图形中去探寻问题解决的关键，提升学生的解题质量和效率.如此一来，就可以借助整体思想的合理应用来简化学生的解题步骤，提升学生的解题效果.

由此可知，通过在解题过程中合理运用整体思想，可以极大地提升学生的解题质量和效率，培养学生的整体思想和意识，使他们可以灵活地将整体思想合理应用于数学解题中来，从而充分发挥整体思想在提升学生解题能力和效率方面的积极作用.

二、丰富应用方式，提升解题效率

整体思想在数学解题中的应用，关键在于暂时忽略将复杂的局部，从整体角度来解决有关的数学问题，其可以极大地简化解题流程，降低解题的难度，提高学生解题的准确率.但是整体思想的应用方式众多，不单单局限于某一种单一的应用方式，所以在学生充分了解和掌握整体思想来解题的方法之后，为了进一步提升学生的解题效率，就必须要丰富整体思想的实际应用方式，具体包括代入、配对、变形和换元等方式，但是无论采用何种应用方式，必须要从整体角度来对待求解的数学题目进行仔细观察和分析，同时需要确保计算过程中问题转化的等价性，避免因不等价的转化而影响实际的解题效果，下面结合具体的例题来详细地探讨整体思想的具体应用效果.

（1）整体思想在补全式子中的应用，其主要是将整体思想合理应用于数学问题的解题中，通过补充题干中尚未完整的式子来达到简化待求解问题的目的.

例3 求sin220°+cos250°+sin20°cos50°的值.

分析：该道三角函数的题目看似只是简单的函数值求解问题，如果单纯地用配方或者万能法来进行逐个分解、组合来求解，那么需要涉及大量计算，并且会增加计算的出错率，此时如果可以借助整体思想的合理运用，那么就可以通过将该公式补充成三角函数计算的标准形式，从而达到简化解题的目的，具体解题过程如下：

解：假设A=sin220°+cos250°+sin20°cos50°，

B=cos220°+sin250°+cos20°sin50°，那么可知：

（2）整体思想在参数代换中的应用，其主要是将整体思想合理应用于数学问题的解题中，通过替换题干中相应公式的某些参数来达到简化待求解问题的目的.

分析：该道题目是一道典型的三角函数代换问题，其中涉及到x和y两个参数，单纯地采用配凑法那么会影响解题的效率，增加出错的概率，此时如果可以合理运用替换法，那么就可以极大地提升该道例题的解题质量和效率.

解：假设μ=cosx+cosy，分别平方已知式和待求式，那么可得：然后将两式进行相加可得

另外，针对上述问题，如果单纯地依靠自身条件无法求解，可以尝试采用整体代换的方法来进行问题的求解.

（3）整体思想在换元中的应用，其主要是将整体思想合理应用于数学问题的解题中，通过采用换元的方法来达到简化待求解问题的目的.

例5 已知x，y∈R+，x2+y2=1，求x+y+xy的最大值.

分析：该道例题是一类求解函数值的问题，其中由于涉及到“平方”和“1”这些敏感的题干信息，所以此时教师可以引导学生来合理运用三角换元等方法来达到简化解题的目的.

（4）整体思想在配方中的应用，其主要是将整体思想合理应用于数学问题的解题中，通过采用拼凑等配方方法来达到简化待求解问题的目的.

分析：针对该种类型的数学问题，需要先转换解题思想，找到解题突破口，然后需要采取整体的配方，采用放缩法来对有关的问题进行合理解决.

（5）整体思想在求导中的应用，其主要是将整体思想合理应用于数学问题的解题中，通过采用求导等方法来达到简化待求解问题的目的.

分析：该道题目是一道典型的函数问题，并且涉及到恒成立的问题，此时如果单纯地进行函数简化运算，或者数形结合等方法来求解，计算量均比较大，但是此时如果教师可以引导学生运用整体思想，则可以帮助学生深入挖掘解题的重要信息，使学生快速找到突破口，以便达到解决问题的目的.

由此可知，该类问题涉及到参数和不等式恒成立问题，此时教师要告诫学生一定要做好相应的分类讨论工作，并在此基础上来罗列相应的解题不等式，在其中贯彻整体思想观念来达到提高解题有效性的目的，增强学生学习知识的兴趣，提升他们的学习效果和创新能力.

（6）整体思想在转化中的应用，其主要是将整体思想合理应用于数学问题的解题中，通过采用转化方法来达到简化待求解问题的目的.

例8 求tan20°+tan25°+tan20°tan25°的值.

分析：该道题目也是一道典型的三角函数题，其中涉及到的角度都是不常见的角度，所以无法进行单个进行计算，必须要从整体上考虑这些角度之间的关系.通过观察不难发现，其中20°和25°之和为45°，所以需要就如何将它们联系起来来进行思考.而通过整体思想的贯彻，可知需要先转化有关的读数来求出相应的函数值.

解：已知tan45°=tan（20°+25°）=1，并且tan（20°+25°）由此可知：

tan20°+tan25°+tan20°tan25°=1.

针对上述类型的高中数学类型题，教师在平时要注重整体思想的贯彻，同时要做好相应的针对性训练，以便可以更好地提升学生应用整体思想来解决有关数学问题的熟练度，提升学生的解题能力.

总之，高中数学知识涵盖的内容多、范围广，并且其中有大批高难度的抽象型数学问题，此时如果学生缺乏科学的解题思路以及高超的解题技能，那么势必会影响学生的解题效果.而整体思想在高中数学解题中的合理渗透，可以逐步帮助学生树立科学的解题思路，优化学生解题流程.但是为了充分发挥整体思想在提升学生解题能力的积极作用，教师必须要结合教学内容和学生学习情况下综合确定，从而全面提升学生解题能力.