例谈构造函数证明不等式问题的若干途径

☉浙江省诸暨市湄池中学 蔡旦燕

例谈构造函数证明不等式问题的若干途径

☉浙江省诸暨市湄池中学 蔡旦燕

中学数学中的一个难点是不等式问题，近几年的高考热点中不等式所占的比例也一定程度上在增加.而函数思想已成为整个中学数学的重点和高考的热点.有些不等式采用常规方法难以解决，若能巧妙地构造函数将不等式问题转化为函数的问题，通过研究辅助函数的单调性、极值、最值等问题，常能使问题获得简捷明了的解决.笔者通过平时的教学实践从以下几个方面加以解读，试图破解此类问题.

一、根据式子特征联想构造函数证明不等式

很多不等式证明题的结构有一定的特征，经常可以根据式子特征构造函数.数列的递推公式是给出数列的一种方式，其实这其中也蕴含着函数，数列就是由这个函数来发生的，若能联想到这个函数往往也能抽象的数学问题变得简单直观.

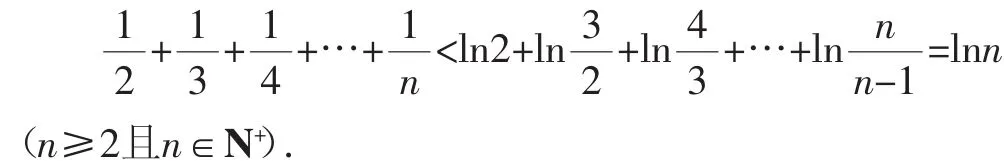
点评：不等式两边是n-1项和的形式，而lnn是Sn的形式为了消除这种形式上的不和谐，我们尝试把“lnn”还原成n-1项和的形式，设Sn=lnn，则an=Sn-Sn-1=lnn-ln（n-1）=从而我们就探寻是否有的成立？

二、构造“带参数型”函数利用导数求最值

0cosx0-c=0.

x （0，x0） x0 x0，π 2（）g′（x） → 0 →g（x） ↗ ↘

因为g（x）在区间［0，x0］上是增函数，所以g（x0）＞g（0） =0.进一步，“g（x）＞0对任意恒成立”当且仅当0，即

三、利用换元构造函数证明不等式

有的不等式具有某些函数类似的结构特征，使人很自然地联想到某类函数，通过换元能使函数特征更加清晰，故称其为“换元法”.

点评：我们知道，当F（x）在［a，b］上单调递增，则x＞a时，有F（x）＞F（a）.如果f（a）=φ（a），要证明当x＞a时，f（x）＞φ（x），那么，只要令F（x）=f（x）-φ（x），就可以利用F（x）的单调增性来推导.也就是说，在F（x）可导的前提下，只要证明F′（x）＞0即可.

四、分清主次，选择主元构造函数证明不等式

有的题目字母繁杂，若分不清主次，则显得扑朔迷离，不得要领，但只要确定一个字母为主变量，即主元，则辅助函数唾手可得，问题便迎刃而解，故称之为“主元法”.

例4 已知函数g（x）=xlnx，设0＜a＜b，证明：0＜g（a）+

证明：对g（x）=xlnx求导，则g′（x）=lnx+1.

当0＜x＜a时，F′（x）＜0，因此F（x）在（0，a）内为减函数；

当x＞a时，F′（x）＞0，因此F（x）在（a，+∞）上为增函数.

从而当x=a时，F（x）有极小值F（a）.

因为F（a）=0，b＞a，所以F（b）＞0，即g（a）+g（b）-

当x＞0时，G′（x）＜0.因此G（x）在（0，+∞）上为减函数.

因为G（a）=0，b＞a，所以G（b）＜0，即g（a）+g（b）-

点评：对于多变量型问题绝大部分学生都会望而生畏.学生的困惑主要就在于不能直接使用所给函数.如果能挖掘一下所给函数与所证不等式间的联系，想一想大小关系又与函数的单调性密切相关，由此就可过渡到根据所要证的不等式构造恰当的函数，利用导数研究函数的单调性，借助单调性比较函数值的大小，以期达到证明不等式的目的.

五、利用二次求导构造函数证明不等式

在一些问题中，一次求导后函数的单调性、极值等性质还不明显，必须构造函数进行二次求导判断.

（Ⅰ）若f（x）在R上为增函数，求a的取值范围；

（Ⅱ）若a=1，求证：x＞0时，f（x）＞1+x.

解：（Ⅰ）f′（x）=aex-x，

因为f（x）在R上为增函数，所以f′（x）≥0对x∈R恒成立，即a≥xe-x对x∈R恒成立.

构造函数g（x）=xe-x，则g′（x）=e-x-xe-x=（1-x）e-x，

当x＞1时，g′（x）＜0，当x＜1时，g′（x）＞0.

故g（x）在（-∞，1）上为增函数，在（1，+∞）上为减函数，所以当x=1时，g（x）取得最大值，即所以即a的取值范围是

则F′（x）=ex-1-x.

令函数h（x）=F′（x）=ex-1-x，则h′（x）=ex-1.

当x＞0时，h′（x）＞0，所以h（x）在（0，+∞）上为增函数，

又h（x）在x=0处连续，所以h（x）＞h（0）=0，

即F′（x）＞0，所以F（x）在（0，+∞）上为增函数.

又F（x）在x=0处连续，

所以F（x）＞F（0）=0，即f（x）＞1+x.

点评：当函数取最大或最小值时不等式都成立，可得该不等式恒成立，从而把不等式的恒成立问题可转化为求函数最值问题.不等式恒成立问题，一般都会涉及到求参数范围，往往把变量分离后可以转化为m＞f（x）或m＜f（x）恒成立，于是m大于f（x）的最大值或m小于f（x）的最小值，从而把不等式恒成立问题转化为求函数的最值问题.因此，利用导数求函数最值是解决不等式恒成立问题的一种重要方法.

六、通过等价转化，间接构造函数证明不等式

数学问题的复杂多变使函数的构造方法呈现出多样化的特点，因此，我们必须开阔视野，随机应变，其中一个重要的策略就是转化，等价转化也是极为重要的一种数学思想.

大家知道，用导数研究函数的单调性、极值、最值等问题是高考中常考的内容，在这类大题的考查中常常会伴有不等式证明，以及解不等式.用构造函数，运用导数的方法，来解（证明）不等式，会使这类表面抽象、相对复杂的题目变得直观和简单.

（Ⅰ）讨论函数f（x）的单调性；

（Ⅱ）证明：若a＜5，则对任意x1，x2∈（0，+∞），x1≠x2，有

这里，仍然只研究第（Ⅱ）问.

解析：（Ⅰ）略.

所以只需要证明函数g（x）=f（x）+x在（0，+∞）单调递增即可.这样，便有以下解题思路：

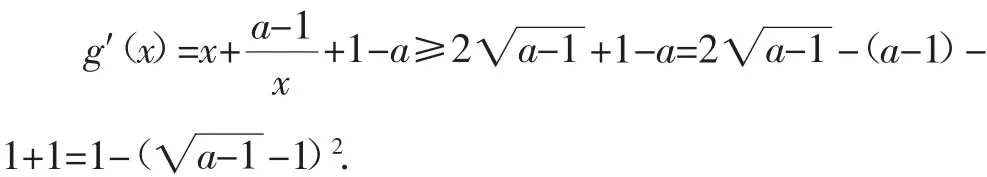
因为1＜a＜5，因此g′（x）＞0，所以g（x）在（0，+∞）内单调递增，

从而当x1＞x2＞0时，有g（x1）-g（x2）＞0，也就是f（x1）-f（x2）+x1-x2＞0，

点评：从上例的解题过程，我们不难发现，只要从需要证明的或已知条件给出的不等式入手，将不等式的一边化为0，另外一边分母是x1-x2，分子中的函数即是要构造的函数.当我们构造出了适当的函数，再运用函数的单调性就能很好地解决这样的问题了.通过这道例题，我们也看到：借助第一个问题来构造具体函数，顺利解题，不失为一种解题的好方法.

总之，构造函数具有一定的创造性，需要相当的技巧，一般来说可以从待证不等式形式变化的角度和所含“元”的个数来考虑构造方法.如果面对的是另类的陌生情境，题目本身没有给出所用方法的暗示，那么我们就需要根据问题的特征机智巧妙地迁择证法.总之，在面对一个个具体问题时，我们不应肓目地套用已有模式，而应根据题目，灵活变通，多管齐下，多法并用.