“动中寻静，动静结合”破解高中数学动态难题

☉江苏省姜堰中学 李 彦

“动中寻静，动静结合”破解高中数学动态难题

☉江苏省姜堰中学 李 彦

从哲学的角度来看，动与静是相对矛盾的统一体，动态问题是高中数学教学中的难点问题，在处理高中数学的动态问题时，采取“动中寻静，动静结合”的处理方法与手段，能够有效突破思维障碍，准确把握切入点，弄清解题的方向；笔者根据自身的教学实践，以高中数学动态问题为探究载体，采取理论与案例相结合的方式，重点阐述紧抓运动中的不变量，采取动静结合与转换的具体实施方式，希望能给读者带来一定的参考与借鉴.

一、动中寻静，以静制动

运动是绝对的、永恒的，而静止却是相对的，自然界的万物都是处于运动之中；在数学领域之中，数量关系与空间形式变换体现运动的特征，但在运动的、变化的过程中蕴含着静止的、不变的因素；实践表明，以数量关系与空间形式中的不变量为解题的突破口，能够提升处理数学动态问题的实际效率.

例1 如图1所示，正四棱锥P-ABCD可以绕AB边任意旋转，AB⊂平面α，已知点P在平面α上的射影为O，试求：|OC|的最大值.

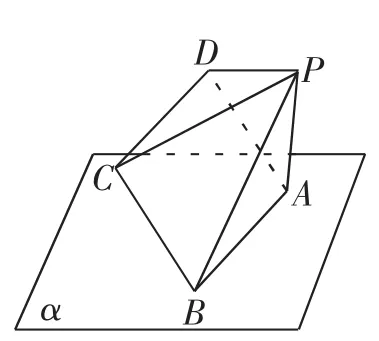
图1

图2

解法1：根据题意作出如图2所示的辅助线，E、F、M分别为AB、CD、PE的中点，点O为P点在平面α上的射影且在线段AB的中垂线上，CD⊥面OEF，正四棱锥绕AB边旋转的过程中，OM和MF的长度保持不变且|OM|=在 Rt△OFC中，|OC|2=|OF|2+|CF|2，由于|OF|≤|OM|+|MF|，则，则当O、M、F三点共线时，|OC|取得最大值且

解法2：正四棱锥P-ABCD在绕AB边旋转的过程中，向量和的模，以及与、与之间的夹角均为确定值，令∠PEO=α，根据几何关系知∠PEF=60°，则当2θ=90°，即θ=45°时，|OC|2取最大值且

点评：本题主要涉及立体几何动态旋转中的极值问题，由于动点O和C位置的不确定性，从而导致不少学生难以准确找到解题的突破口；解法1中解题的关键在于从运动旋转中不变量OM和MF入手，构建直角三角形进行求解，体现了“动中寻静，以静制动”的处理手段；在求极值时特别要注意一种错解的情况：|OC|≤|OM|+|MF|=3（此时取等号的情况不成立）；解法2中，借助于向量的分解进行运算，形成“以静制动”的解题效果，能够有效化解动态旋转难题.

二、动静转换，化繁为简

从物理学的角度来看，运动和静止具有一定的相对性，参照物的不同运动的特征也不相同，在数学数量关系中A相对于B运动（A动B静止）可以看成B动A静止；对于数学中的动态问题，完全可以利用这种动静之间的相对性进行处理，往往能够达到意想不到的效果.

例2 在平面直角坐标系中，存在如图3所示的圆M：（x-3）2+（y-3）2=4，E为圆内接正方形ABCD边AB上的中点，若正方形ABCD绕圆心M转动的同时点F在边AD上运动，试求：的最大值.

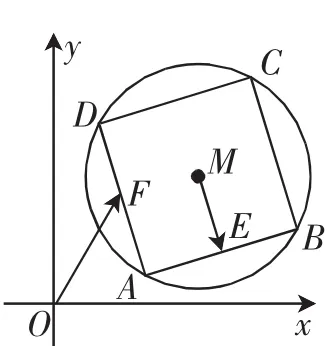
图3

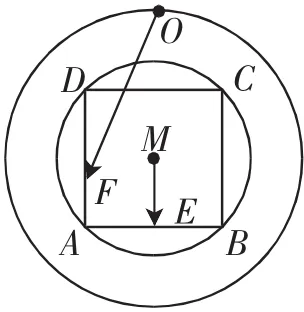
图4

解法2：原题中正方形ABCD绕圆心M旋转，坐标原点O不动；这里可以看作正方形ABCD固定不动，坐标原点O以M为圆心，OM为半径做圆周运动，如图4所示，从数量积的几何意义角度分析，当O、M、E三点共线且F点运动至A点处时，向量在向量方向上的投影值最大，则此时取最大值，即

点评：本题主要考查向量中的极值问题，解法1的主体思想是进行向量的分解与转化，过程复杂烦琐，对学生的向量运算和思维能力要求较高，部分学生难以准确、快速地处理本题，显得“力不从心”，而解法2将研究对象进行有效转换，将多点运动的问题转化为单点运动的问题，卸下复杂外衣，化繁为简，极大地降低原题的难度，从而实现从“疑无路、柳暗”向“花明”的有效转化.

三、动静结合，事半功倍

运动与静止是矛盾的统一体，同时存在，同时制约，两者还可以相互转化；实践表明，灵活处理好数学问题中的“动”与“静”之间的关系，能够准确把握住数学问题的本质，加深对问题的进一步理解，提纲挈领，顺利解题，从而达到“事半功倍”的效果.

例3 已知函数f（x）=x2+mx-1满足在x∈［m，m+1］上使得f（x）＜0均成立，试求：实数m的取值范围.

例4 已知0＜x1＜1，0＜x2＜1，0＜x3＜1，试求证：x1+x2+x3-x1x2-x1x3-x2x3＜1.

证明：令x3=x，f（x）=（1-x1-x2）x+x1+x2-x1x2，则命题变为证明：f（x）＜1，若1-x1-x2=0，则f（x）=x1+x2-x1x2=1-x1x2＜1；若1-x1-x2≠0，由于函数f（x）是单调性函数（一次函数）且f（0）=x1+x2-x1x2=（1-x2）（x1-1）+1＜1，f（1）=1-x1x2＜1，综上可得f（x）＜1，即x1+x2+x3-x1x2-x1x3-x2x3＜1.

点评：函数是高中数学教学中的重点、难点和热点问题，例3中主要是针对二次函数最值问题的考查，这里是采取“轴动——‘动’，取值区间定——‘静’”的手段进行处理，“一动一静，动静结合”的方式，结合二次函数的性质可知，二次函数的最大值出现在取值范围的端点处，这样能给有效避免分类讨论，化繁为简，让问题“迎刃而解”；例4中，涉及的参数变量比较多（三个变量），直接利用不等式的性质进行解题几乎是无从下手，毫无头绪，给不少学生带来解题的麻烦，这里若固定变量（x1和x2——“静”），有效引入新的变化参量x（令x=x3——“动”），将原题转化成函数问题，再利用函数的性质进行分析证明结论.

总而言之，“动静结合”是一种典型的数学思想和解题方法，实践表明，利用动静结合的数学思想方法分析实际问题时，能够有效转化问题的实质，有助于探寻高中数学动态难题的入手点和突破口，有利于把握数学问题的本质规律；作为一线的高中数学教师，在平时的教学中，应该有意识地培养学生“动中寻静、化动为静、动静转换、动静结合”的数学思想方法，促进学生个性品质的快速发展，进而提升高中数学课堂教学效益.