一道数学高考选择题的破解感悟

☉湖北省监利县第一中学 张江松 苏贤昌

一道数学高考选择题的破解感悟

☉湖北省监利县第一中学 张江松 苏贤昌

深入研究数学高考选择题，不仅能提高我们解题的技能技巧，优化解法思路，还能夯实基础，促进创新思维，拓展知识视野，提升解题能力.考基础，考能力，一直倍受数学高考命题者的重视与青睐.2016年新课标（Ⅰ）理数学高考试题第12题就是一道考基础、考能力的典型试题.该题立足教材，涉及知识点多，综合性强，匠心独妙，解法要求独特.现将本题的几种破解思路的感悟——活算、细算、验算、测算，与读者分享.

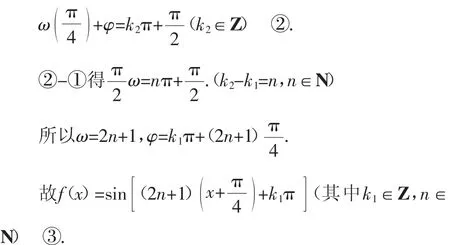
由函数的单调性得

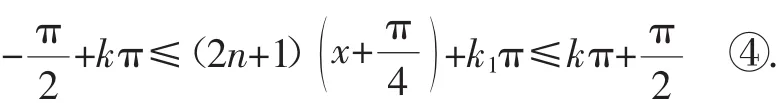
结合选项易知，（2n+1）必为36的因数，由此可得n= 4.

至此便可确认ω=9.

所以选B.

解法2：上接④，得

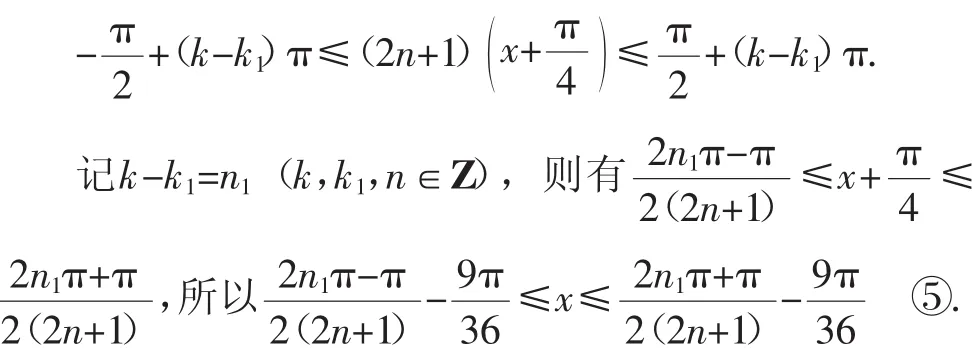
因为ω=2n+1，于是，结合选项可得n∈［1，5］.

由此不难发现，当n=4，n1=3时，⑤式可变为

所以选B.

此时x0正好是区间右端点.

至此，便可作选择了，故选B.

结合选项知，n的范围是1≤n≤5.

所以ω的最大值为9，故选B.

解后反思：本题主要考查三角函数图像的零点、对称轴及单调性，考查运算能力及推断能力.

实际上，作为完整的解答，在（※）式后应加上：当n= 4时，区间的左端点为

解法2抓住③式探究，获得⑤式，并由此推得函数f（x）的单调区间为再确认所给的区间是它的子集而获解.思维严谨，颇有逼上梁山之意.体现了“细算——支干关系若明了，直接演算巧推导”的战术思想.

解法3是以对称轴为主，用希望的眼光来探究的，在求解时并未面面俱到，一解到底，体现了“测算——假设猜想助思考，目测试探亦为招”的战术思想.

解法4思路的来源，是在求出ω=2n+1后，为了避开对条件“（fx）在上单调”直接推理而产生的.这种作法充分体现了“验算——由干推支不易表，反推筛选亦是道”的战术思想.

不难发现，对n=5时的情形的处理，还可从对称轴（或极值）的角度来考查，从而获得如下解法.

“活算”、“细算”、“验算”、“测算”是解答本选择题的基本方法.当然对数学选择题的解法还有：估算、图算、巧算及逻辑分析法等，这些有待读者去探究.