从一道试题的挖掘谈试题结构分析

☉山东省青岛第九中学 段旭东

从一道试题的挖掘谈试题结构分析

☉山东省青岛第九中学 段旭东

众所周知，数学学习成绩的提高离不开试题的训练.回头望望，传统的成绩提高训练离不开大量试题的训练，即所谓的题海训练战术.这在新知教学以及高一、高二教学中的确起到了一定的作用，也是很多教师屡试不爽的教学法宝之一.随着数学知识难度的增加，这种题海训练模式的弊端迅速在高三教学中显现出来，其一是各种各样的试题太多，学生的学习时间有限，不可能把所有的试题面面俱到地解答一遍，而且很多试题没有价值，浪费了时间和精力；其二是没有思考的训练，没有挖掘的练习，往往导致了学习的低效性，这些现象的改变需要在学习中精选问题，在有限的时间内做好高效复习.

近期笔者在一次课后提问中，尝试了对一个问题的深入思考和探索，与同学们一起研究试题处理的角度和多样性，深刻体会了罗增儒教授所描述的“题不在多，有深究则灵”这一话语，让笔者对于如何思考问题、解决问题以及对问题培养专研精神有了更多的收获.

问题：已知（fu）=u2+au+（b-2），其中x≠0），若a，b可使方程f（u）=0至少有一个实数根，求a2+b2的最小值.

当4-|a|≥0和a2-4（b-2）≥0时，则2|a|≥b+2，若b+2≥ 0，则即当若b+2＜0，则a2+b2＞4（舍去）.

当4-|a|＜0和a2-4（b-2）≥0时，a2+b2＞16（舍去）.

评析：本题是笔者在复习中，引入的一个函数零点问题.这是标准答案提供的解法，仔细一看该解法也比较工整，推理也比较严密，分类切入也比较合理，是一个不错的解决方案.但有的同学会问笔者：这个方法要求根，很啰嗦，有没有更好的解法呢？笔者陷入了思考.我们解决问题有时因为种种原因，总是陷入标准答案之中，用他人的思考替代了自己的思维，这种“照搬答案”的解法自然是无法吸引同学们积极学习数学的兴趣，因为笔者认为应该从一个值得研究的问题入手，合理探究、共同探讨，培养问题思考角度的多样性和探究的理性精神.

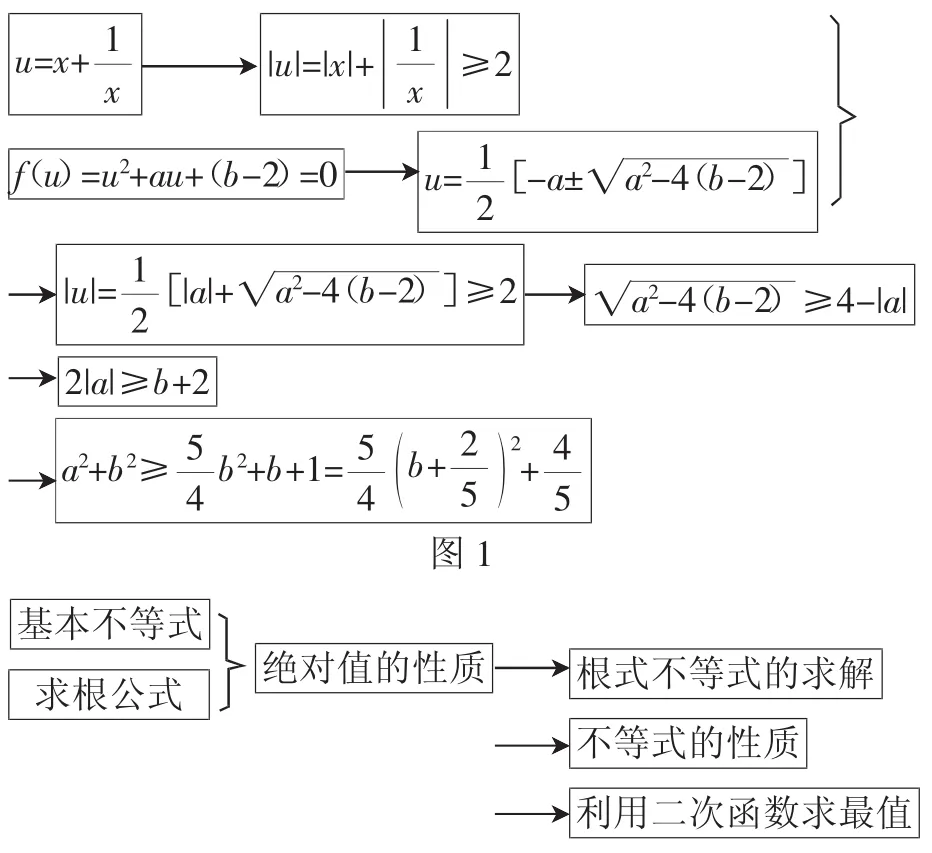
重新思考：本题的变量较多，但是按照次序和整体性而言，首先应该考虑u，从这一字母出发，进而思考a，b，最后解决a2+b2.即（1）求出u的值域；（2）从f（u）=0的根u的范围来得到a、b所满足的条件；（3）求出a2+b2的最小值.笔者将知识处理的流程用框架结构展示出来（如图1所示），大家可以清楚地看到问题处理所需要的流程，以及所运用到的基本知识和基本技能（如图2所示）.

结构分析：（1）上述解法采用了最直接的思路，利用f（u）=u2+au+（b-2）=0的根得到绝对值不等式，进而转化为无理根式不等式解决问题，但是无理根式处理的难度较大，一般学生只能放弃，因此从理论上可行但是学生实际操作困难重重；（2）上述解答中第二问起到了承上启下的作用，是关键步骤；（3）上述解法是从正面入手，环环相扣.

解题反思：从正面角度入手，思维量比较简单，但是运算比较复杂，很明显同学们很难从这样的运算中得到最终的答案.那么我们应该思考另一个问题：是不是有更佳的入手角度呢？从哲学角度来说，解决途径正难则反易，是不是换一个角度来得更为容易呢？

从上面的结构分析中可以看到，原解法中有三个未知数，a、b、u，在原解法中突出了u的地位，强调了u的优先使用权，a，b退居二线，所以我就以它们的地位不同得到下面的结构特征.

第一问的情况较简单，我们分析的重点放在第二问和第三问，在第二问的解决中始终围绕f（u）=u2+au+（b-2）=0至少有一实根，它的结构特征的探讨如下：

特征1：u2+au+（b-2）=0看成关于u的一元二次方程，在这里突出u的地位.

特征2：f（u）=u2+au+（b-2）看出二次函数y=f（u）与u轴的交点的个数至少有一个，在这里还是突出u的地位.

特征3：u2+au+（b-2）=0处理成一个恒等式问题，a，b，u地位是相同的.

特征4：u2+au+（b-2）=0关于a，b的直线方程，把u看成常数，a，b地位突出.

与此同时，第三问a2+b2的最小值的解决办法将决定整个解题的方向，下面a2+b2的最小值就本题而言体现选取的策略如下：

特征5：a2+b2的最小值转化为二次函数问题来解决.

特征6：利用基本不等式来求解a2+b2的最小值.

特征7：利用a2+b2的几何意义来解决a2+b2的最小值.

在这里多种特征方式的出现，体现了知识间结构的清晰度和连通性，同时也开辟了解题途径的多样性，为我们下面的新解法做好基础性的铺垫.从我们的上述分析的主要本质步骤和第二问中的特征1、2、3、4以及第三问的特征5、6、7重新组合为更接近问题的深层结构的新解法.

评析：本题的解法是特征3和特征5、6的资源重组，利用恒等式的恒等变化为关于a的一元二次函数来求解，最后利用基本不等式来求解，最大的优点避开了烦琐的分类讨论，但在式子上过于复杂，没有扎实的基本功是解不出来的.

所以得到f（u）=0至少有一根在平面直角坐标系中表示的区域为（*），其中（*）为表示区域的补集.

利用线性规划知（*）表示的线性区域如图所示：图中阴影部分表示a、b的满足的范围，由几何意义知a表示点（a，b）到原点距离的平方.从图像观察，原点到线形区域上的点（a，b），是点到直线2a+b+2=0或者2a-b-2=0的距离的平方最短.易由解析几何知识知d2=时取等号.

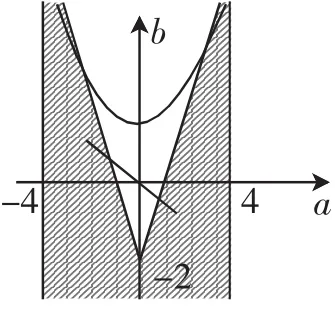
评析：此题的解法是常规解法，大部分师生做到第二问的a，b所满足的（*）式，接下去求a2+b2的最小值感觉无能为力，如果没有对a2+b2的最小值的探索是得不到这个解法的.所以我们感到有必要实施解题分析.从而我们另辟新径利用a2+b2的几何意义，结合线形规划知识（本质是数形结合），使问题得以顺利解决.

评析：此题的解决是在新解1和新解2的前提下，寻求的新的解法.题目的解决关键是把u2+au+（b-2）=0看成关于a，b的直线方程.这正是由于我们对题目反思的结果.既简化计算，又是思维清晰.不失为一种最佳答案.

小结：根据上面的分析，我们可以感到解题分析的重要性和功效.也初步了解了如何进行解题分析.下面简单概括以下几点.

（1）确定一个分析的视角：分析的角度可以是多方面的，本例的分析角度选取了这样一个模式：提出问题—问题特征—策略选择—资源配置—反思回馈.

（2）解题分析的收获：我们从上面的分析可以得到以下几个方面的成果.

从微观层面上，将有助于理解问题的深层结构，不仅能简化过程、完善解题，而且会产生陈题新解、难题简解、佳题巧解等效果；

从宏观层面上，将有助于数学解决问题能力的提高，具体表现为问题的识别和结构特征，将有助于解题思路的主动设计，方法的灵活运用；

总之，解题后一定要进行解题分析和解后思.一思，解决对的问题，二思，解决优化，三思，解决通法.在分析和反思的过程中不断总结方法、技能以及经验教训，真正领悟到数学思想和本质问题，优化认知结构，提高思维能力，从而更大的发挥和提高同学们的智力和潜能.