一道无理型三角形不等式及其衍生

☉浙江省湖州市双林中学 李建潮

一道无理型三角形不等式及其衍生

☉浙江省湖州市双林中学 李建潮

问题1（《数学通报》2015年9月号问题2263 以下称问题2263）在△ABC中，求证：

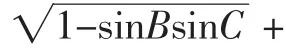
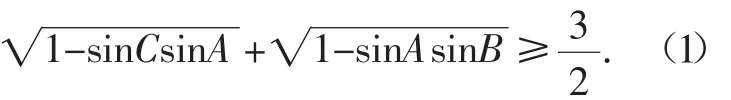
本人在对问题2263的证法探究中不经意间获得了它的加强；“无意插柳”间优化了数学通报的其他个别问题；在类比中，衍生出新的无理型三角形不等式……

一、问题2263的新证与加强

新证：在△ABC中，

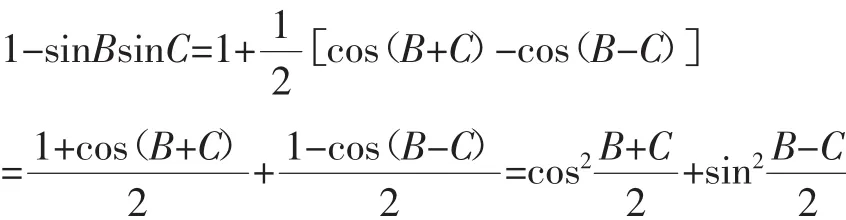
结合二维柯西（Cauchy）不等式（a2+b2）（c2+d2）≥（ac+bd）2，有

同理

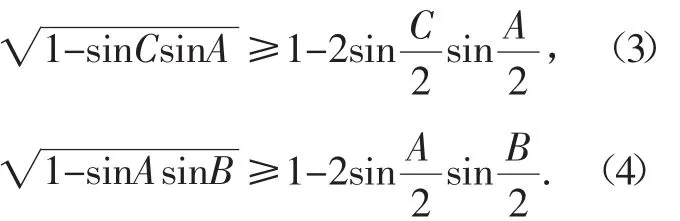
（2）+（3）+（4），并利用文［1］三角形不等式：

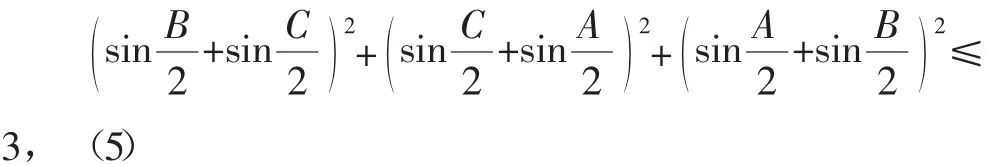
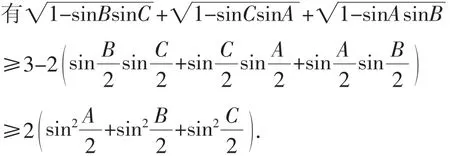
据此，问题2263加强为：

定理1 在△ABC中，有

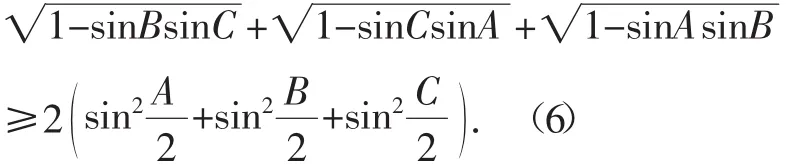
二、问题2263的弦“外”之音

问题2 设△ABC的外接圆和内切圆半径分别为R、r（本文下同），证明：

（《数学通报》2007年8月号问题1779）

问题3 在△ABC中，求证：

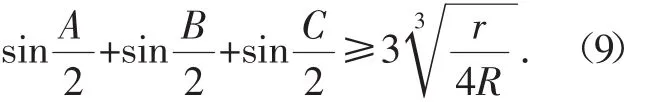
（《数学通报》2012年9月号问题2083）

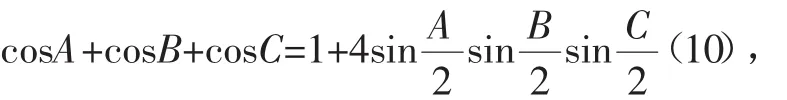
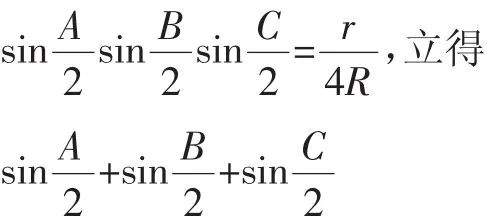
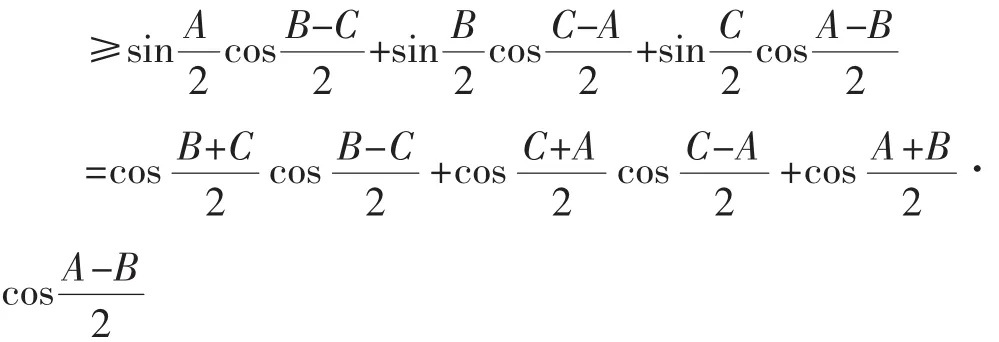
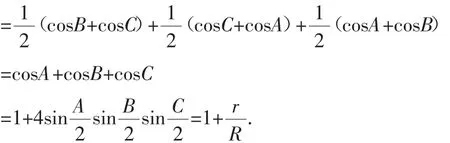
所以，问题2与问题3可一并优化为：

结论1 在△ABC中，有

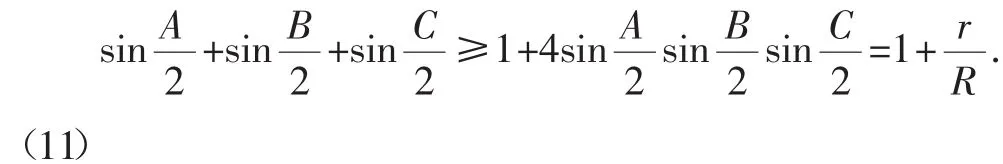
顺水推舟，看下述问题：

问题4 在锐角△ABC中，试证：

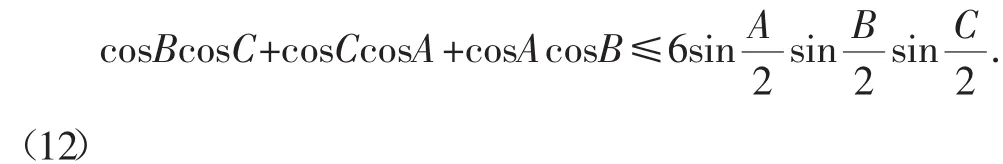
（《数学通报》2005年7月号问题1561）

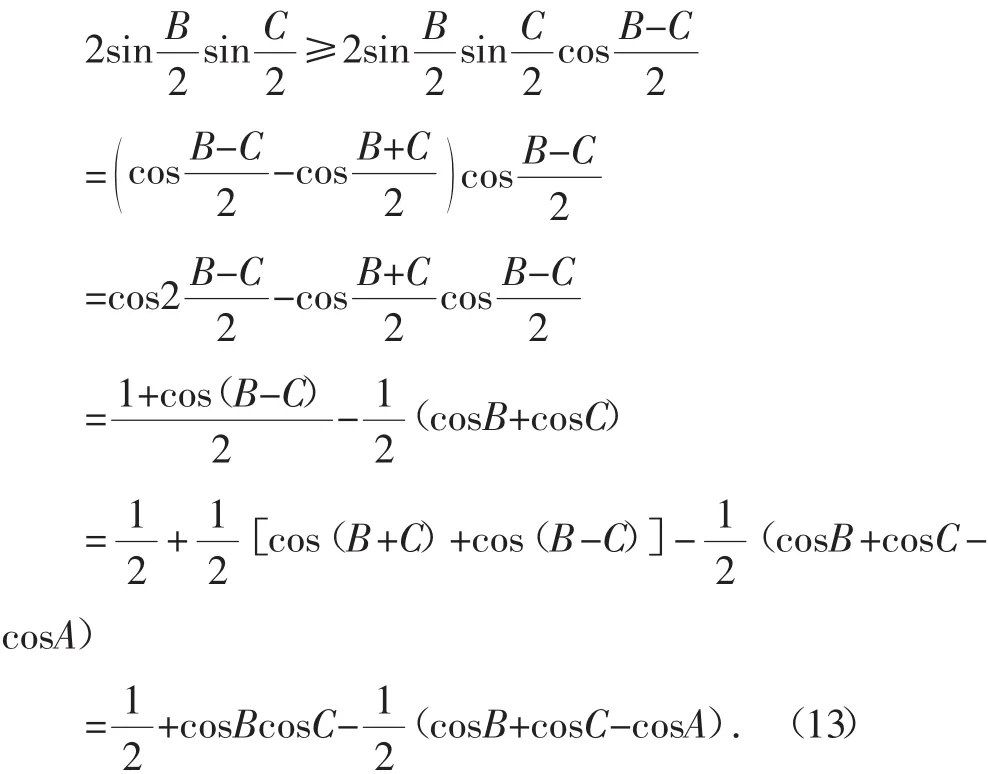
同理

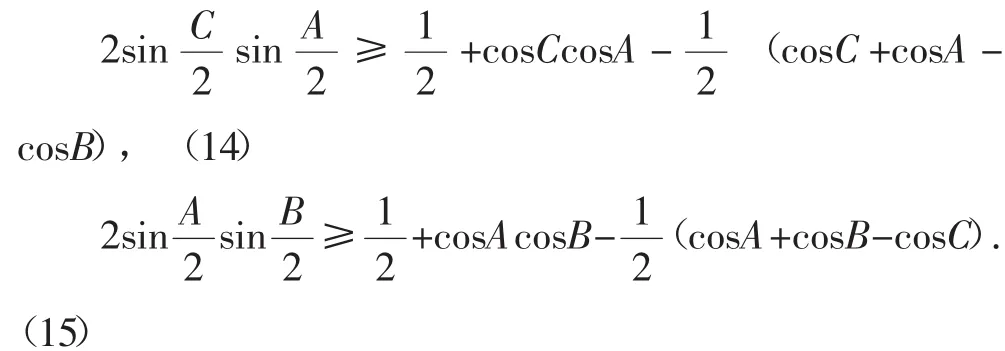
（13）+（14）+（15），并应用（5）、（7）与（10）三式，可得

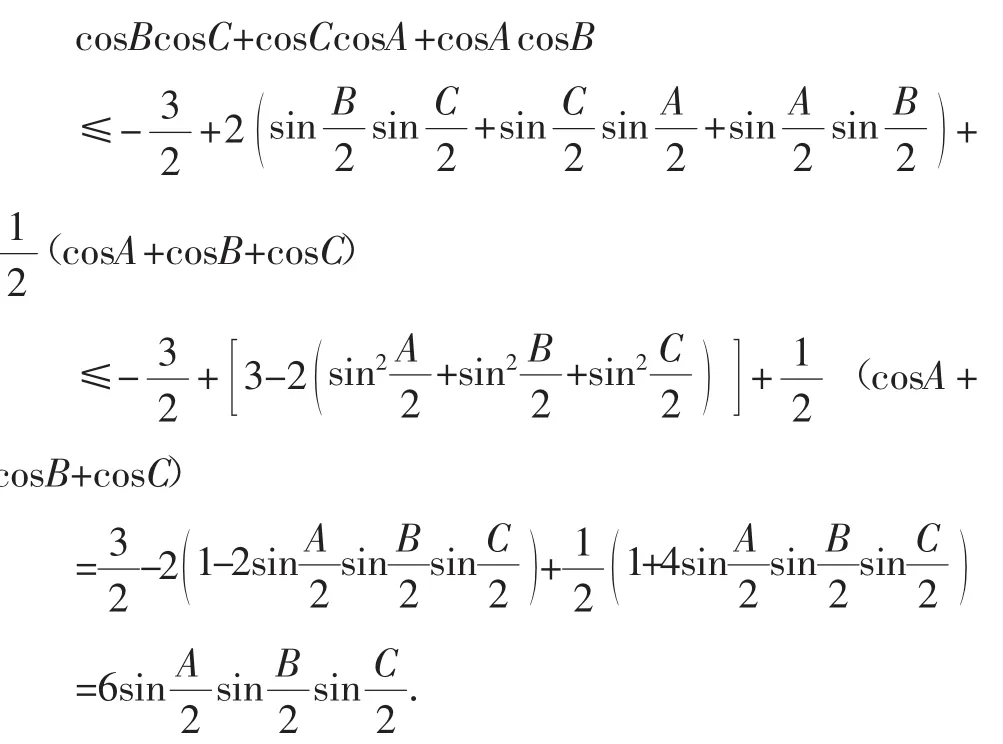
从以上分析看，并没有用到“锐角三角形”条件，所以，问题4可优化为：

结论2 在△ABC中，有

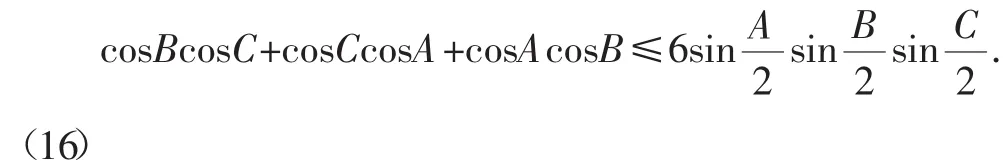
三、问题2263的衍生

无独有偶，作为问题2263的类比，我们自然提出下述问题：

问题5 在△ABC中，证明或否定：

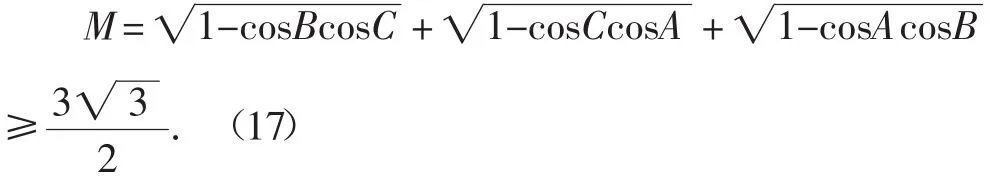
笔者试图仿照问题2263的证法去获取证明，但没有成功.转而又尝试用平方法，终于大功告成.其间需要下述中间结论：

定理2 在△ABC中，有

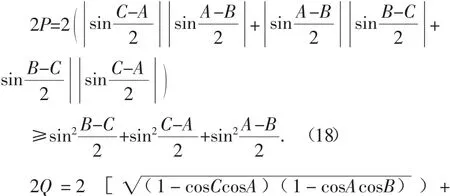
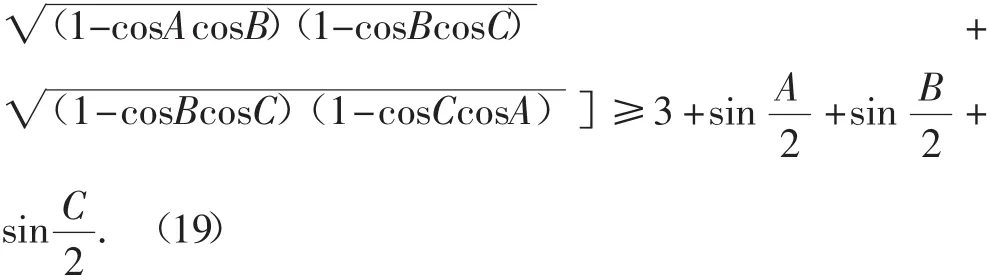
证明：先证（18）：

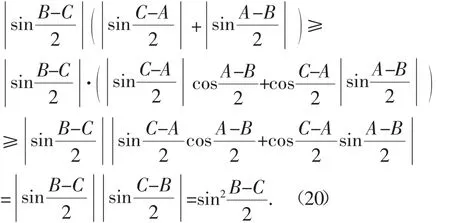
同理

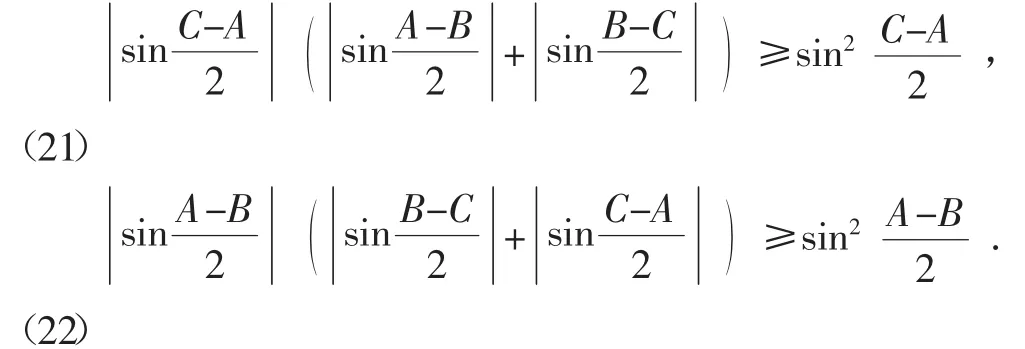
（20）+（21）+（22），（18）式获证.

再证（19）：

仿问题2263证明，并应用（18）式，有

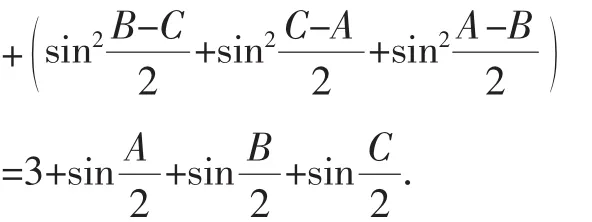
定理2获证.

下证问题5（即（17）式）：由结论2、定理2的（19）式及结论1，可得

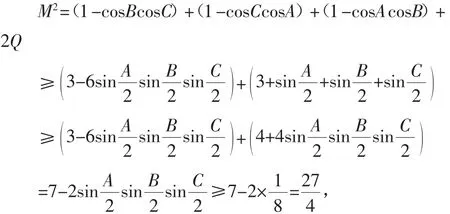
定理3 在△ABC中，有

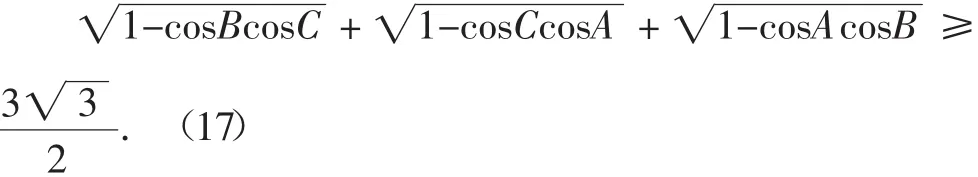
四、问题2263的又一个加强

由定理2（19）式的成功建立，用类似的证明方法不难获得问题2263的下述又一个加强：

定理4 在△ABC中，有

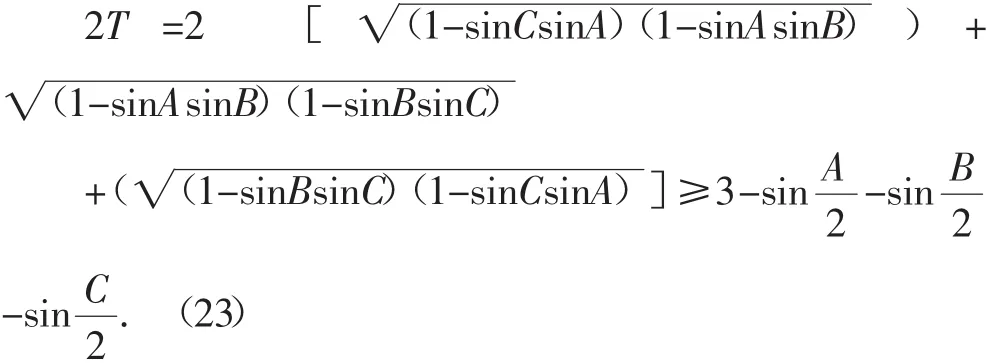
并且Q+T≥3（其中Q的意义同定理2的（19）式）.

本文值得注意的一个地方是定理2的（18）式的构想与创立（她是获取定理3的基石），实乃是向“0”要“正数”的一种奇特数学思想，堪称不等式证明之精髓.

1.李建潮.一个数学问题的“热能”效应［J］.数学通报，2008（6）.

2.许雪芬，李建潮.由一个三角形不等式引发的探究［J］.中学数学（上），2015（11）.