联想，让解题更自然——一道三角形中三角问题的解题教学探究

☉江苏省南通市天星湖中学 葛建华

联想，让解题更自然
——一道三角形中三角问题的解题教学探究

☉江苏省南通市天星湖中学 葛建华

三角问题是高考数学中的必考问题，在填空题和解答题中都有体现，常常被认为只需掌握三角公式和几个定理即可，但实际上在解题时，如果角度选得不对，往往绕半天也解不出结果.最近笔者在整理高三必考问题时，发现一道三角形中的三角问题，与学生一起多角度探讨并进行了有效拓展研究，再现当时的过程，与同行探讨.

一、问题呈现

题目：在△ABC中，角A，B，C满足lgtanA+lgtanC= 2lgtanB，则角B的取值范围是__________.

二、师生探讨

（一）阅读问题，尝试解题

让学生仔细阅读题目，并认真分析，稍给一点时间做一些思考，尝试独自解决.由于题干比较简短，学生似乎马上就读懂了，也匆匆就下手解题了.

师：此题中条件有何特点？怎么处理？有什么注意的？问题的解决需要先解决何问题？

生1：条件是含对数的等式，首先要去掉对数，真数均为正，在三角形中，可知三个内角都是锐角，再找与角B有关的条件进行转化.

对学生给予肯定后，发现学生马上就能得到tanA· tanC=tan2B，但接下来似乎很难往下继续了.

（二）深入问题，把握本质

师：三角形中角可以由什么来刻画即角具有什么本质？求角B的范围，应先求什么？注意什么？

生2：三角形中的角是三角形本身决定的，本质上某个角可由其他的角来刻画或由边来刻画.常常是先求角B的某个函数（如tanB或sinB或cosB）的范围，注意三角形的形状和角的大致范围，再结合条件求出角B的准确范围.

（三）多角度研究，寻求解答

师：根据三角形中角的本质，可以从什么角度研究？对式子tanA·tanC=tan2B又如何处理？

生3：可以从角或边的角度来考虑了.由于是正切的式子，所以可以从函数名角度分析应该有两个角度：切化弦和直接用正切解决.

1.切化弦角度

生4：可以将正切化为正余弦，再运用积化和差公式，利用内角和A+B+C=π将三个角进行转化，求sinB或cosB的范围，再求出角B的准确范围.

解法一：由题可知，tanA·tanC=tan2B，切化弦得，整理得cos（A+C）=cos（A-C）cos2B，从而有-cosB=cos（A-C）（2cos2B-1），即由题易得

小结：将对数运算等价转化后，由正切联想商数关系，采用“切化弦”的策略，利用余弦函数的有界性求范围，角本身的范围也是一个不容忽视的方面.

2.角化边角度

师：三角形中角的正余弦除了利用三角公式解决外，还能借助三角形中其他元素来解决吗？求cosB的范围还可以利用什么来解决？

生5：可利用正余弦定理，将角转化为边来处理，借助于边的关系求出cosB的范围.

解法二：由题可知，tanA·tanC=tan2B，切化弦得利用正余弦定理可得化简得从而因此可得角B的取值范围是

师：试比较解法一和解法二，各有什么优缺点？

生6：在三角形中，实现边角互化是解决问题的常用方法，对于解法一需要三角公式准确变形，简洁；解法二利用角化边处理，避免了三角公式，需要代数运算变形，有时可能比较烦琐.

3.方程角度

师：从正切角度如何解决？可否从正切有关的三角公式入手？

生7：有两角和的正切公式，可以很容易得到tan（A+ C）=-tanB，再求出tanB的范围，从而可求出角的范围，但接下来似乎不容易转化，不知从哪个角度解决.

让学生把能得到的写出来观察，再将得到的结论进行变式，于是得到tanA·tanC=tan2B，①tanA+tanC=-tanB·（1-tan2B）.②

师：观察①②式，将tanA，tanC的和与积都表示成了含tanB的式子，我们会联想到什么？

生8：韦达定理，所以可以把tanA，tanC看成某个二次方程的两个根，再利用二次方程根的分布解决.

解法三：由题可知，tanA·tanC=tan2B，由tan（A+C）=可知tanA+tanC=tan（A+C）（1-tanAtanC），所以tanA+tanC=-tanB（1-tan2B），从而tanA，tanC可看成方程x2+tanB（1-tan2B）x-tan2B=0的两个根，且由题可知均大于0，故

小结：借助两角和的正切公式的变式建立了tanA· tanC与tanA+tanC和tanB的关系，联想到二次方程中韦达定理，从而转化为含tanB的方程的根，再利用二次方程有两正根的等价条件解题.

4.数列角度

师：观察tanA·tanC=tan2B左右两边的结构形式，还能联想到什么？

生9：tanA，tanB，tanC成等比数列，可以借助等比数列的知识来解决.

解法四：由题可知，tanA·tanC=tan2B，故tanA，tanB， tanC成等比数列，设公比为q（q＞0），则qtanB.

小结：从式子的结构形式联想到等比数列，再巧妙地利用数列知识将角A、C转化为公比q和角B的正切，从而得出tanB的范围得出结果.

5.基本不等式角度

师：重新审视tanA·tanC=tan2B和tanA+tanC=-tanB·（1-tan2B），从和与积之间的关系，我们还会联想到什么知识来求出tanB的范围？

生10：可以利用基本不等式，直接建立关于tanB的不等式.

解法五：由题可知，tanA·tanC=tan2B，而tanA+tanC= tan（A+C）（1-tanAtanC）=-tanB（1-tan2B），由题易得tanA＞ 0，tanC＞0，tanB＞0，所以2|tanB|=2tanB，从而有-tanB（1-tan2B）≥2tanB，不难得出从而得到角B的取值范围是

小结：由三个正数tanA、tanB、tanC与等式的形式（和积式）联想到可用基本不等式建立tanB的不等式.

6.减元思想角度

师：刚才我们从三角形中三角知识角度，三角公式及其变式角度进行了思考，进行多角度研究，那么对于多元的等式关系求某个变量的范围问题，能否从数学思想角度考虑呢？

张明楷教授认为：民众的舆论与社会的稳定密切相关，当民众普遍认为一个罪犯应当判处死刑，由于没有判处死刑而引起公愤时，决策机构总会担心民众在舆论上的公愤转化为现实社会秩序的不稳定，因而要求对罪犯判处死刑，从而平民愤，保稳定[5]543-556。这说明，在适用死刑的过程中，大众的普遍心理预期直接影响到了刑罚的确定。

生11：我们要求角B的范围，可以消去角A或角C，但利用内角和关系只可以消去一个角，故可以消去角C，从而得到一个关于角A和角B的方程，再利用方程的根的问题来解决.

解法六：由题可知，tanA·tanC=tan2B，即tanA·［-tan（A+B）］=tan2B，所以整理可得tan2A+（tanB-tan3B）tanA+tan2B=0，从而关于tanA的方程在 （0，+∞） 上至少一根，故可得从而不难得到角B的取值范围是

小结：多元问题从数学思想角度不难联想到减元思想，在三角形中利用内角和进行消元使得三元变两元，再将两变量分别看成未知量和参数构造方程来解决.

7.特殊化角度

师：作为填空题，可否“猜”结果呢？

生12：从tanA·tanC=tan2B中发现角A和C地位相同，可以令A=C来探求角B的最值.

解法七：由tanA·tanC=tan2B，令A=C得tanAtanA= tan2B，可知tanA=tanB，即从式子本身来看，角B是中间角，此处最值应该为最小值，由于三角都为锐角，故可猜得角B的取值范围是

（四） 方法总结，比较反思

让学生回顾此题的解决角度和途径，并比较各种解法的优劣，总结解决此类问题的常规有效的方法.

小结：对于给出条件关系求角的范围问题，要善于观察并灵活运用三角公式，往往先求函数值范围再求角的范围.解法一、解法二思路较容易想到，虽变形比较复杂，但不失为一种常见思路；解法三、解法六虽然都是借助方程来解决，但切入口不同；解法三、解法四、解法五都来源于对中间结论中式子形式的观察，选择了合适的角度并运用相应知识解决，构思巧妙，解答简单完美；解法七虽是一种猜的办法，但也是有一定依据去猜的，所以对填空题来说也不失为一种讨巧的方法.

三、拓展研究

师：我们可否变换此题条件，再进行研究呢？

生13：（变式1）在△ABC中，角A，B，C满足tanA· tanC=tan2B，则角B的取值范围是__________.

解析：由于在三角形中，tan2B＞0，可知tanA，tanC同号且均大于零，类似解法四可知，tanA+tanC=tan（A+C）若tanB＜0，则-tanB（1-tan2B）≥-2tanB，所以tan2B≤-1不成立，故tanB＞0，不难得到角B的取值范围是

点评：去掉了对数的外衣，似乎少了一些限制，但利用三角公式进行推理，发现条件并未减弱，这其实都缘于三角形内在的制约，所以挖掘隐含条件也成为解三角问题的一大关键.

师：观察条件特征，刚才同学将条件变成等比数列形式，是否还有可以有其他变形，再探究呢？

生14：（变式2）在△ABC中，角A，B，C满足tanA+ tanC=2tanB，则角B的取值范围是__________.利用例题中解法不难得到角B的取值范围是

师：类比等比数列来研究等差数列似乎很自然，通过研究，发现虽然条件发生变化，但结论并没有改变，这也是三角的魅力所在.前面几种变式都是等式，能否变成其他条件呢？或者结论也能不变呢？

生15：（变式3）在△ABC中，角A，B，C满足lgtanA+ lgtanC≥2lgtanB对任意的角A，C都成立，则角B的取值范围是__________.

略解：利用两角和的正切公式和不等式可得tanAtanC≥3，由tanA·tanC≥tan2B对任意的角A，C都成立，可得3≥tan2B，即从而可得角B的取值范围是

生16：（变式4）在锐角△ABC中，角A，B，C满足tanA+ tanC≥2tanB对任意的角A、C都成立，则角B的取值范围是__________.类似地得到角B的取值范围是

点评：由等式条件变为不等式条件，探求范围变得更复杂，于是增加为恒成立条件得以解决，这也正体现了数学中的辩证统一.

四、反思提升

让学生回顾解决此题和变式探究的研究过程，总结解题研究的思维模式.

生17：思维过程：

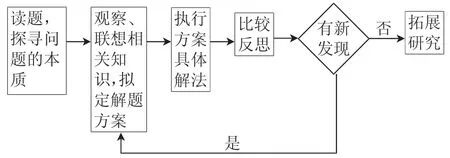
师：很好！这正是我们解题研究的一般模式，以后我们将可以进行有效的自我解决和研究问题.

经过刚才的研究，学生拓展研究的热情并未消减，思绪飞得很远，将条件中正切函数变为正弦和余弦函数并做了探索研究和猜想，然后分组研究得出下面一些条件不同而结论相同的探索问题，由于篇幅关系仅给出正弦的命题，证明过程从略.

探索问题：在△ABC中，角A、B、C满足条件①sinA· sinC=sin2B，条件②sinA+sinC=2sinB，条件③sinA·sinC≥sin2B，条件④sinA+sinC≥2sinB中的任何一个条件时都可以得到角B的取值范围是

点评：由于三角形中利用正余弦定理可以实现边角的转化，因此解决问题很多时候可以用边来解决，但遗憾的是缺少了正切和差角公式中一致性（都是正切），所以如果运用正弦和差角公式则增加了运算转化的难度.

例题中将对数相加转化为真数相乘，从而去掉对数符号，如果改为对数相乘，那又如何处理呢？将正切函数改为正、余弦函数是否也有类似的结论？学生于是又大胆的进行了改变条件和猜想，于是又有了下面变式题留到课后继续研究：

变式5：在△ABC中，角A、B、C满足lgtanA·lgtanC= lg2tanB，则角B的取值范围是__________.

变式6：在△ABC中，角A，B，C满足lgtanA·lgtanC≥lg2tanB对任意的角A、C都成立，则角B的取值范围是__________.

五、教法感悟

1.解题需要先探寻问题的本质，进行本原思索，方能本原解题

《普通高中数学课程标准（实验稿）》中明确指出，数学课程应强调对数学本质的认识与理解.解题时必须从问题的本质角度出发寻找思路，进行本原解题，所以首先要充分熟悉题目，探寻问题的本质，搞清概念的本质和问题的已知与未知的本质联系.联想就是要让思维接近自己的“最近发展区”，所以学生对原有知识的学习与掌握是前提，只有对一些公理、定理、定律、公式等的彻底理解，并能灵活运用才能产自然的联想.

2.多角度研究已知条件，适时追问促进联想寻求解题思路

单墫先生说：“解题到底靠什么？我靠的也就是平常的、普通人的常识.”［1］就是说要自己动手解题，寻求问题中的知识与自己掌握的知识的联系点，从而产生联想，并能运用所掌握的知识、技巧解题，这样才能进行多角度研究.在解题教学中，教师也要适时进行必要的追问，激活学生的思维，进行多角度研究.如例题中我们通过多角度观察联想涉及了三角、数列、不等式、函数与方程等多种知识，解决了恒成立、角的范围问题，渗透了类比、减元、等价转化、数形结合等思想和特殊化处理问题的方法，体现研题的一般思路，拓宽解决问题的角度.

3.加强解题后的回顾与反思提升，做到知其然且知其所以然

解出问题只是对某个问题的解决的结束，但数学题有太多，甚至可以说是“题海”，我们不可能将所有问题都做一遍，所以就有必要对自己做的问题进行及时回顾与反思.要想让学生形成这种习惯，教师就必须要求学生解题后进行反思，弄清自己解决的是什么问题？有哪些角度？哪几个是关键步骤？为什么这样做？审视刚才的解法中的缺陷和优点，这样才能弄清一类问题，让学生体会到：“没有任何一个题目是彻底完成了的.总还会有些事情可以做；在经过充分的研究和洞察以后，我们可以将任何解题方法加以改进；而且无论如何，我们总可以深化我们队答案的理解.”［2］

4.激发学生的探索热情，进行有效拓展研究

学生的潜力是无限的，学习和探索的热情是很高涨的，这些都需要教师积极的挖掘和适时有效的评价.数学问题的解决离不开思考，数学的魅力离不开发现，若能从解题过程中多角度研究，不断深入探索，将问题进行变式研究或推广，我们将有更多的创新和收获.当然要能引导学生进行思考和自主探究还需要教师自身的提高，研究题目应成为我们数学教师的解题习惯，多角度发散考虑，深度思考，探究问题，有利于提高我们自身的数学素养，才更有利于提高课堂教学的有效性，提升学生的核心素养.

1.单墫.我怎样解题［M］.哈尔滨：哈尔滨工业大学出版社，2013.

2.波利亚.怎样解题［M］.涂弘，冯承天，译.上海：上海科技教育出版社，2015.

3.刘智娟.注重高中数学解题中的“四大法宝”［J］.中学数学（上），2014（12）.

4.葛建华.让“研题”成为数学教师的解题习惯［J］.中小学教学研究，2013（7）.