高考立体几何试题的特点分析

☉江苏省海安县立发中学 季小冬

高考立体几何试题的特点分析

☉江苏省海安县立发中学 季小冬

立体几何是高中数学的主干内容，在高考命题中常以一大一小两种题型出现.小题通常考查空间平行或垂直关系的判定、简单几何体表面积或体积的求解、三视图.大题通常考查空间平行或垂直关系的证明、空间角或空间距离问题的求解.下面就这些考题的命题视角举例剖析.

一、以定理及其基本图形为基础

以空间位置关系中的平行和垂直为例，平行（垂直）关系主要包括线线平行（垂直）、线面平行（垂直）、面面平行（垂直）.应用中要把握每种关系应具备的条件以及三者之间的相互推导.

例1已知直线l、m，平面α，且m⊂α，那么“l∥m”是“l∥α”的（ ）.

A.充分不必要条件 B.必要不充分条件

C.充要条件 D.既不充分也不必要条件

解析：本题考查了线线平行与线面平行之间的关系，线与平面平行应具备的条件是已知线不在平面内，而且与已知面内的某条直线平行.

已知条件中m⊂α，且l∥m，但并没有说明直线l不在平面α内，所以不能保证l∥α.

另外，l∥α，由线面平行的性质，经过l的平面且与α相交所得交线与l平行，但m不一定为交线，所以也不能得出l∥m.

故正确选项为D.

例2已知m，n为异面直线，m⊥平面α，n⊥平面β，直线l满足l⊥m，l⊥n，l⊄α，l⊄β，则（ ）.

A.α∥β，且l∥β

B.α⊥β，且l⊥β

C.α与β相交，且交线垂直于l

D.α与β相交，且交线平行于l

解析：因为m，n为异面直线且m⊥平面α，n⊥平面β，所以α与β相交.为了体现题目条件的线面关系，我们可构造空间图形（如图1）：

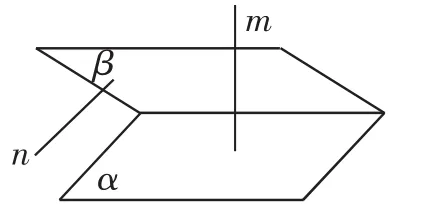
图1

因为直线m⊥平面α，则m与α内的直线或与α平行的直线均垂直；

同理直线n⊥平面β，则n与β内的直线或与β平行的直线均垂直.

所以直线l可能为平面α与β的交线，也可能是与交线平行的直线.又l⊄α，l⊄β，

故正确选项为D.

评析：通过构造出空间图形，将复杂的线、面关系直观地体现出来.在各种关系的性质或判定中要准确把握它们所具备的条件及其相互推导关系.

二、以空间想象能力为依托

考试大纲中明确提出高考命题要体现对考生空间想象能力的考查，而立体几何试题就肩负着这一重任.

例3（2016年全国卷Ⅰ）平面α过正方体ABCDA1B1C1D1的顶点A，平面α∥平面CB1D1，平面α∩平面ABCD=m，平面α∩平面ABB1A1=n，则m，n所成角的正弦值为（ ）.

解析：根据题目条件可构造出相应的正方体，但平面α并没有在正方体中体现，如何构造出平面α是问题求解的关键.

如图2所示，以A为顶点再补一个全等的正方体ADEF-A1D1E1F1，则易证EF1∥CB1，AE∥B1D1，则平面AEF1∥平面CB1D1，而平面AEF1过正方体的顶点A，故平面AEF1就是平面α，而平面AEF1∩平面ABCD=AE，平面AEF1∩平面ABB1A1=AF1，则m，n所成角就是直线AE和AF1所成的角即∠EAF1，而△AEF1为等边三角形，因此故正确选项为A.

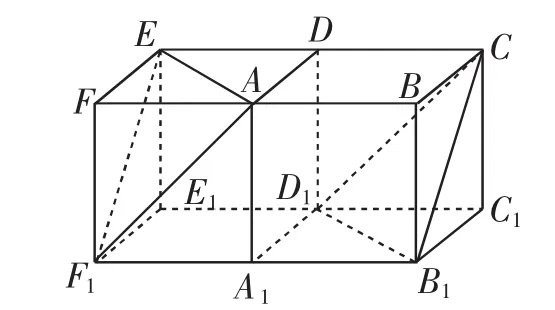
图2

评析：对于没有给出图形的立体几何体问题，准确构图是问题求解的关键，能充分考查考生的空间想象能力.

三、以位置关系转化为基本思维模式

解决立几问题除了要熟练掌握立体几何的基础知识、要有一定的空间想象能力外，还要掌握重要的数学数学方法“转化与化归”，能把空间问题转化为平面问题、把面面关系转化为线面关系、把线面关系转化为线线关系，以及通过等体积转化法来求解相关问题.

例4 （2016年全国卷Ⅲ）如图3，四棱锥P-ABCD中，PA⊥平面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点.

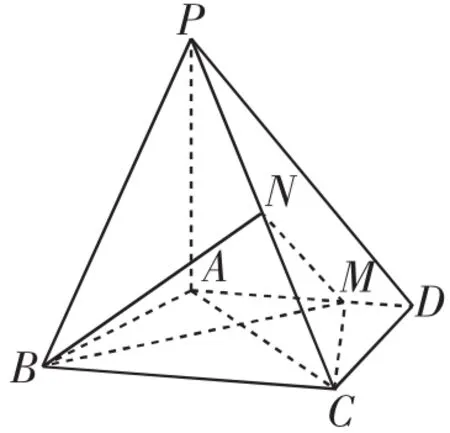
图3

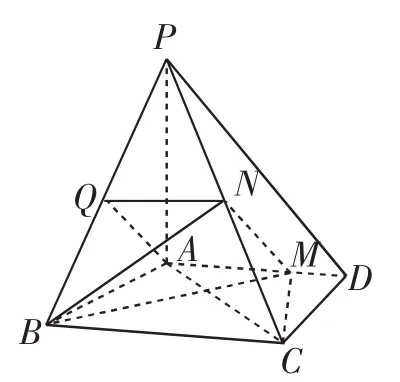
图4

（1）证明MN∥平面PAB；

（2）求四面体N-BCM的体积.

解析：（1）证明：如图4，取PB中点Q，连接AQ，NQ，因为N是PC中点，NQ∥BC，且NQ=2，BC，而且AM∥BC，所以QN∥AM且QN=AM，所以AQNM是平行四边形，即MN∥AQ.

又因为MN⊄平面PAB，AQ⊂平面PAB，

所以MN∥平面PAB.

（2）由（1）知QN∥平面ABCD，所以VN-BCM=VQ-BCM=所以

评析：第（1）问欲证一条直线与一个平面平行，只要证明此直线与平面内某一条直线平行即可.通过利用三角形的中位线来构造辅助线不仅顺利证明了第（1）问的结论，也为第（2）问等体积的转化法的运用创造了有利条件，从而使问题得到圆满解决.

四、以几何法与向量法为手段

空间向量的引入使得在立体几何的教学中出现了重视计算，消弱了空间想象力能力培养及推理教学的现象，致使考生推理证明、空间想象的能力有所下降，这就要求我们在教学中对高一必修阶段立体几何初步的定位要因学生情况而适当调整.

例5（2016年浙江卷）如图5，在三棱台ABC-DEF中，平面BCFE⊥平面ABC，∠ACB=90°，BE=EF=FC=1，BC=2，AC=3.

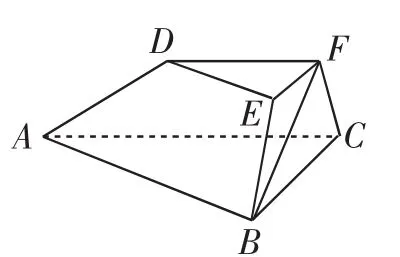
（1）求证：EF⊥平面ACFD；

（2）求二面角B-AD-F的平面角的余弦值.

解析：（1）证明：如图6，延长AD，BE，CF相交于一点K.因为平面BCFE⊥平面ABC且AC⊥BC，所以AC⊥平面BCK，所以BF⊥AC.

又因为EF∥BC，BE=EF=FC=1，BC=2，所以△BCK为等边三角形，且F为CK的中点，则BF⊥CK，所以BF⊥平面ACFD.

（2）方法1（几何法）：如图6，过点F作FQ⊥AK，连接BQ.

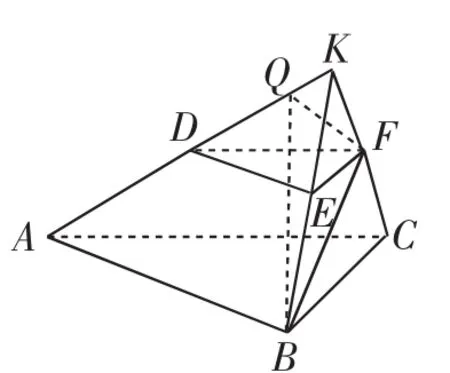
图6

因为BF⊥平面ACK，所以BF⊥AK，则AK⊥平面ΒQF，所以BQ⊥AK，所以∠ΒQF是二面角BAD-F的平面角.

方法2（向量法）：如图7，取BC的中点O，则KO⊥BC，又平面BCFE⊥平面ABC，所以KO⊥平面ABC.以点O为原点，分别以射线OB，OK的方向为x，z轴的正方向，建立如图7所示空间直角坐标系O-xyz.

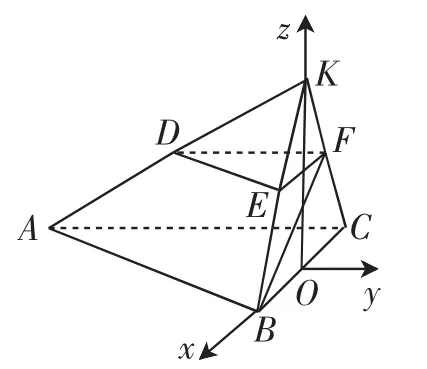
图7

设平面ACK的法向量为m=（x1，y1，z1），平面ABK的法向量为n=（x2，y2，z2）.

评析：无论求直线和平面所成的角，还是平面和平面所成的角，通常有几何法和向量法.在几何法中对于角的计算，一般是把所求角进行转化，体现了化归与转化思想，主要是将空间角转化为平面角.如求线面角，关键是找斜线在平面内的射影；而求二面角，应先找到两个平面的交线，分别在两个平面上向交线作垂线，则这两条垂线的夹角就是所求的二面角的平面角.向量法则可建立坐标系，利用向量的运算将线面角转化为直线的方向向量与面的法向量的夹角，对于二面角则转化为两个面的法向量的夹角求解.用向量法可避开找角的困难，但计算较繁，所以要注意准确计算.

总之，对于立体几何的复习，要牢固相关的理论基础，清楚命题视角，准确把握构造法、转化法以及向量法，即可以不变应万变实现对问题完美解答.