培养数学空间想象力

陈晨

立体几何是高中数学的重难点之一。本文结合突破空间几何体的截面问题，谈对培养学生空间想象能力的实践与思考。

2020年武汉市高三九月新起点考试第7题（如下图），很多学生不能正确解答。

错因分析：已知直线[l]与平面[a]上一条直线平行，那么直线[l]与平面[a]的位置关系应有两种可能，一是[l？a];二是当[l？a]，[l∥a]。学生不能识别的原因是空间想象能力较差，不能由已知图形作出平面ABC切正方体的完整截面，从而忽视了直线MN在平面ABC内的可能，直接由线线平行到线面平行。

针对学情，笔者希望通过突破空间几何体（以正方体为例）的截面问题，培养学生的空间想象能力。

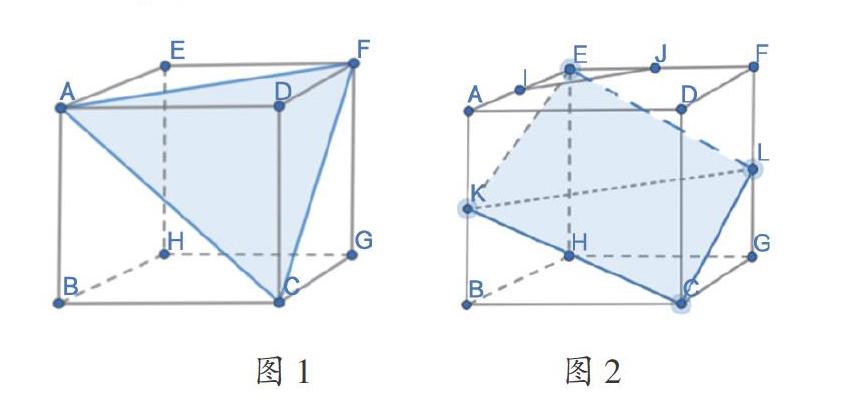
笔者先画出一个正方体，并在上面选择了不相邻的三个顶点，如图1中A、C、F，请学生讨论过这三点的截面的形状。学生很快得出结果：确定截面的形状要点是找到平面与正方体各个面的交线，而确定交线只需找到两个平面的两个公共点，将公共点连接起来就是我们所要找的交线。作出三条交线AF，AC，CF之后，三角形ACF即为完整截面。对于这类比较简单的情形，学生归纳出以下几种方法。

一、直接法

有两点在正方体的同一个面上，连接两点即为截面与正方体的交线，顺次连接各点所形成的平面图形即为截面。

笔者提高难度：以前面所举第7题的A选项为例，如图2，I、J、K、L分别为所在棱的中点，请确定直线IJ和平面KLC的关系。学生很容易证明出IJ与KL是平行的，但此时仍需要判断IJ是否在平面KLC上。因此，下一步目标是确定平面KLC切正方体的完整截面。

在这个过程里，学生遇到一个障碍：当他们用前面的方法顺次连接K、L、C三点的时候，得到了交线KC和LC，但KL并不是平面与正方体表面的交线，于是画出的三角形KLC也并不是完整截面。学生进一步思考，已知侧面AEHB与截面KLC有一个公共点K，则这两个面的交线必过K点。又已知正方体相对的两个面互相平行，那么平面KLC与这两个平行平面的交线一定平行。因此，过K点作出LC的平行线KE，即为交线。学生用同样的方法得到另一条交线LE。此时ELCK构成的四边形就是完整截面，显然IJ直线不在该截面上，因此可得线面平行。

学生继续总结第二种情形：发现当所画出的截面不完整时，需要补全截面，此时需要确定截面所在平面与正方体表面的交线，那么可通过作平行线的方法扩大图中的截面范围。

二、平行线法

过直线与直线外一点作截面，可过该点作直线的平行线，进而找到截面与几何体的交线。

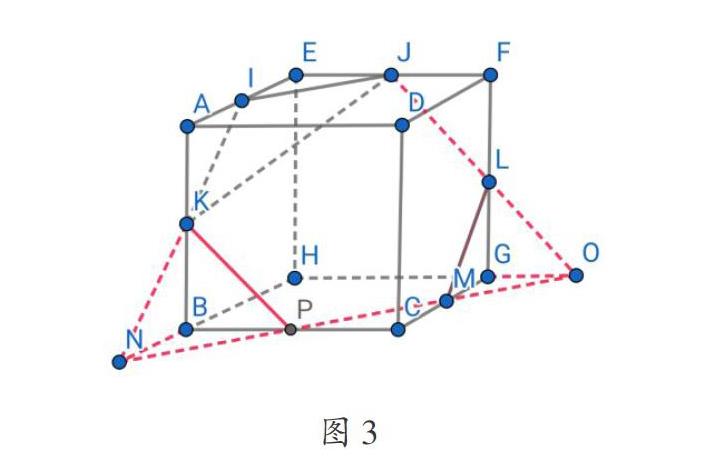
接下来，笔者以D选项为例。如图3，需判断直线LM与平面IJK的关系。

这里学生遇到了更大的障碍，得到交线IK，IJ之后，三角形IJK不是完整截面，并且过J点或K点作平行线也依然不在正方体的表面上，不能直接用平行线法。笔者提示：我们回归问题的本质，找交线问题实际上还是找公共点，现在该如何找到平面IJK和底面BHGC的公共点呢？笔者让学生观察侧面AEHB，显然IK和BH不平行，则它们延长之后必交于一点N。学生发现N点同时属于直线IK和BH，也即同时属于平面IJK和平面BHGC，于是得到了这个公共点。下一步，学生通过平行线法过N点作出IJ的平行线，得到截面与底面的交线NO，交HG延长线于点O，此时O点同时属于直线NO和HG，也即同时属于平面IJK和平面HGFE，O点是平面IJK和平面HGFE的一个公共点，又已知J点也是平面IJK和平面HGFE的一个公共点，则连接JO得到一条交线JL。学生再顺次连接各点得到交线KP，PM，ML，最终得到完整截面为六边形IJLMPK。显然LM在此平面上，不能得到线面平行，因此本题正确答案是D选项。

三、延长线法

将在同一平面上两点连线延长直至与另一个平面相交，得到一个公共点，在同一平面上若有两个公共点，则两点连线为交线。

培養空间想象力的前提是对空间图形足够了解，以及对点线面体这一系列规律的熟练掌握，只有做到这些，学生才能顺利地在脑海中建立起空间模型，帮助他们去理解和解决立体几何的相关问题。