数学“微专题”复习：尺寸之内做文章

☉江苏省淮安市淮海中学 王开林

数学“微专题”复习：尺寸之内做文章

☉江苏省淮安市淮海中学 王开林

传统的数学复习课教学一般是沿袭“练习+模仿记忆”的套路，试图把所学知识点、技能点用题型加以覆盖，将解题策略规则化，以便凭借“面积大”来提升覆盖所考试题.这种复习方式过度强调机械的记忆与模仿，虽然短期效果明显，但容易导致“题海战术”、思维僵化等不良后果.复习不应该只是对已有知识的再回顾，更应该是对知识系统的再建构、再完善.依托主题明确、极具针对性的“微专题”进行复习，可以促进学生的深度学习，从而有利于学生获得清晰的数学知识网络、系统的数学研究方法，加深对数学的理解.“微专题”是指围绕一两个紧密相关的知识或思想方法而形成的一个专项研究.相对于大专题，“微专题”还可以理解为针对某个特定目标，结合学情设计的能够在短时间内专门解决的问题集.“微专题”教学条理清楚不零散，结构简洁有深度，可以做到“简约而不简单”.著名特级教师李金蛟对它的评价是：“切口小，尺寸之内做文章.”①那么，微专题教学到底能做哪些文章呢？

一、“集中火力”，突破难点

讲解面面俱到，“一口吃个胖子”是传统数学复习课的弊端.正所谓“欲速则不达”，数学复习应该“集中火力”，逐个突破难点.微专题的选题不求面面俱到，而是要结合复习的目标要求，针对学生在复习中暴露出的在知识、方法和能力等方面的薄弱环节，以学生复习中的“问题”促“专题”的生成，力求解决学生学习中的难点.

微专题——平面向量共线定理的应用

【精选例题】

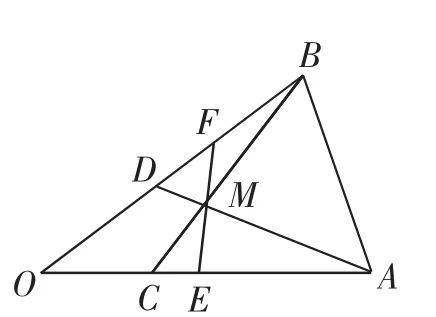
图1

（2）在线段AC上取一点E，线段BD上取一点F，使EF过M点，设求证段AB交于圆内一点M，若则OM的长度为_______.

图2

点评：“平面向量共线定理应用”选题视角比较小，能够凸显“微专题”的特征.此定理的虽然内容简单，但应用广泛，是解决平面几何中点、线位置关系问题的重要工具.对于学生而言，能够理解定理，但无法做到灵活应用.

【变式训练】

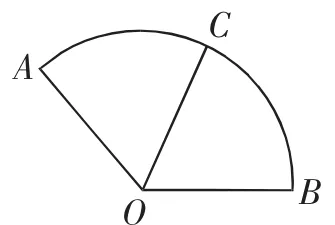
图3

变式2 如图4所示，A、B、C是圆O上的三点，CO的延长线与线段BA的延长线交于圆O外的点D，若则m+n的取值范围是（ ）.

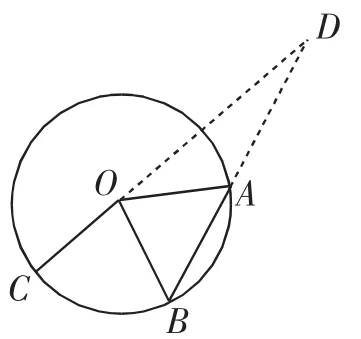
图4

A.（0，1） B.（1，+∞）

C.（-∞，-1） D.（-1，0）

点评：题目的思考角度与解题方法的多样，不会令学生感到无从下手；题目之间具有层次性，由浅入深逐步展开，这种层次不仅体现在逻辑上，还体现出思维生成的层次.两道例题+两个变式，题目数量虽然不多，但它对于“平面向量共线定理”解题功能及应用技巧揭示绰绰有余.

二、“增进互动”，提升效率

复习课的模式很多，它们都有一个共同的特点，那就是学生参与度高.美国学者埃德加·戴尔提出的金字塔理论：对同样的学习内容，读能够记住10%，听能够记

例2 如图2所示，点A、B、C是半径为1的圆O上的三点，线段OC与线住20%，看能够记住30%～50%，这些都是被动学习方式.参与讨论，发言能够记住70%；做报告，给别人讲，亲身体验，动手做能够记住90%，这些是主动学习.“微专题”因其“身轻”而灵活，师生互动多，学生参与率高，突出了学生主动学习与主动探究，因此教学成效突出.

微专题——揭开“分段函数”的面纱

意图：通过“构造”个思维活动既可以呈现学生对分段函数的原有认知，又可以进一步明确分段函数的定义与特征.教师采取了小组合作的探究方式，并且要求每个小组举出符合要求的分段函数.

意图：让学生在构造中主动发现分段函数单调性的实质；通过小组合作学习方式有利于集中群体智慧，快速达成学习任务.

意图：通过增加“原料”函数的数量进一步丰富分段函数的类型，有利于归纳分段函数奇偶性的特点.同样采用小组合作的学习方式，让学生写出尽可能多的符合要求的分段函数.

点评：合作学习可以解决个体无法解决的疑难，通过小组讨论、互相启发，达到优势互补，共同解决疑难.合作学习使学生思维的火花得到完美的绽放，实现了教师与学生、学生与学生、教师与教师的多边互动，从而使课堂呈现百家争鸣的新气象.

三、“构建模型”，优化思维

将复杂的数学问题去掉非本质的部分，抽象出解决问题的思维本质，即“建模”.“模型”是“扶手”，是“台阶”，建立思维模型对知识模块化、能力系统化有着重要作用.数学学习从某种意义上说是模型的学习.教师围绕一些具体问题的解决抽象出数学模型，并结合数学模型的迁移、应用设置“微专题”，有利于学生感悟数学本质，优化解题思维.

微专题——函数模型视角下的等差数列

例1 已知数列｛an｝是等差数列，ap=q，aq=p，且p≠q，求ap+q.

解析：作出等差数列通项公式所表示的函数图像，如图5，通过观察与分析，很容易得到ap+q=0.

图5

问题1 你能从图像解法中看出等差数列的通项具有怎样的本质特征？

问题2（1）等差数列｛an｝的通项一定是关于n的一次函数吗？

（2）an=an+b是｛an｝为等差数列的什么条件？

问题3 能否根据对应的一次函数的单调性判断出等差数列的增减性？

例2 已知数列｛an｝是等差数列前n项和为Sn，Sp=Sq，且p≠q，求Sp+q.

解析：方法同上，通过二次函数图像，直接得到结果.

问题1 等差数列｛an｝的前n项的和Sn一定是关于n的二次函数吗？

问题2 Sn=an2+bn+c是｛an｝为等差数列的什么条件？

问题3 能否利用对应的二次函数的图像和性质求Sn的最值？

点评：以上两道经典习题分别从等差数列的通项公式与一次函数模型的关系、求和公式与二次函数模型的关系入手，让学生结合“问题串”思考、探究，以理解数列的本质是特殊的函数；让学生通过比较，体验利用这种本质特征解数列题的优越性，并了解基本的运用方法，建构等差数列的函数模型，体会数列与函数之间本质的一致性.

“微专题”教学具有“因微而准、因微而细、因微而深”等特点，能起到“见微知著”的作用.利用“微专题”复习要做好以下四个方面的工作：首先，选题应精准，既体现计划性又不失变化性，瞄准重点、难点，教学目标，依据学生的实际需求，设计既有典型性、基础性，又具有拓展性的微专题；其次，对同一个微专题，可能有不同的教学切入点，我们应选择一个适合学生认知规律、有利于揭示题目之间本质联系切入点，这样有助于学生生成对这类问题的整体认知；再次，操作方式要灵活多样，给予学生展示、交流的机会，增加变式，激发学生学习动机；最后，专题复习注重过程管理，学生出现问题要追本穷源，问题的产生是源于思维方式、解题方法还是基础识记，从而有针对性地解决问题.

1.王开林.解题教学活动应注重培养学生的数学思维品质［J］.数学教学研究，2015（6）.

2.殷孝锋.见“微”知著——微专题在数学思维训练中的应用［J］.中学数学月刊，2016（1）.

3.吕增锋，裘燕娜.在构造中发现，在合作中提炼——高一“分段函数”教学尝试［J］.中学数学（上），2016（1）.

4.曾荣.“微专题”复习：促进深度学习的有效方式［J］.教育研究与评论，2016（4）.