根深才能叶茂——基于一类课本习题的探究

☉江苏省宜兴市第一中学 杜亚强

根深才能叶茂
——基于一类课本习题的探究

☉江苏省宜兴市第一中学 杜亚强

数学教学是培养学生运用所学知识解决实际问题的能力，在此过程中提高学生的思维水平，培养学生独立分析问题、解决问题的能力.章建跃博士曾说过“课本是一科之本，课堂教学应‘以课本为本’”.的确，我们从事教学的主要工具——教材，里面有着取之不完、用之不尽的研究素材，笔者通过一类课本习题的研究性学习，取得了一些意想不到的结果，现把它写出来，供共同商讨、研究、学习之用.

一、问题的提出

苏教版《普通高中课程标准实验教科书·数学（选修2-1）》上有这样的几道习题：

习题1：已知直线y=x-2与抛物线y2=2x相交于点A，B，求证：OA⊥OB.

习题2：已知直线y=x+b与抛物线x2=2y交于A，B两点，且OA⊥OB（O为坐标原点），求b的值（.该习题同时也出现在《选修1-1》P60上）

习题3：已知顶点为坐标原点，焦点在x轴正半轴上的抛物线有一个内接直角三角形，直角顶点在原点，斜边长是一条直角边所在直线的方程是y=2x，求抛物线的方程.

这三道习题，分别是课本54页、67页的习题，其都涉及这样一个事实：过抛物线的顶点有两条互相垂直的直线与抛物线相交于另外两点.教材上为数不多的例题习题中，竟然有3道习题涉及同一个模型，应该引起教师学生的注意和重视.

章建跃博士说过：“课本是使学生学做人做事的基本载体，脱离课本的教学不是好的数学教学.”高考试题中有相当一部分试题是对“三基”的考查，虽然不大可能考查课本原题，但许多考题就是对课本原题的变形、改编或者是综合，这些考题都能在课本上找到源头.因此教学复习中，要重视课本，要重视例题习题的通性通法，适当对例题习题进行变式等，进一步落实基础，以不变应万变.

二、问题的探究

探究1：如图1，已知抛物线C：y2=2px（p>0），过原点有两条互相垂直的直线分别交抛物线于A，B两点，试问直线AB有什么特点？

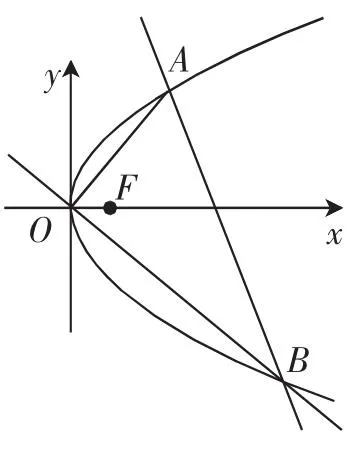
图1

解析：记直线OA的方程为y= kx（k≠0），联立方程消去y得到k2x2=2px，从而有A以代替k，可以得到B（2pk2，-2pk）.当k≠±1时，直线AB的斜率为所以直线AB的方程为即即即所以直线过点（2p，0）.当k=±1时，A，B两点的横坐标都是2p，直线AB也就过点（2p，0）了.所以直线AB恒过定点（2p，0）.

结论1：过抛物线y2=2px的顶点任意作两条互相垂直的直线交抛物线于另外两点A，B，则直线AB过定点（2p，0）.

探究2：如图2，已知椭圆的左顶点为E，过E有两条互相垂直的直线分别交椭圆于A，B两点，试问直线AB有什么特点？

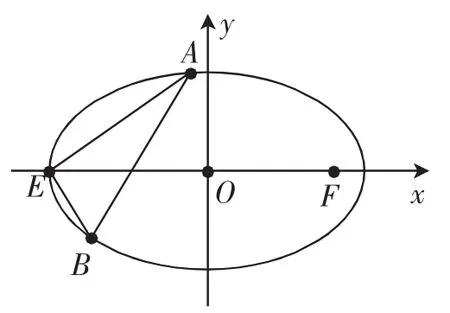
图2

解析：记直线EA的方程为y=k（x+a）（k≠0），联立方程消去y得到（a2k2+b2）x2+2a3k2x+a2（a2k2-b2）= 0，从而有A以代替k，可以得到B当k≠±1时，直线AB的斜率为所以直线AB的方程为即所以直线过点当k=±1时，A，B两点的横坐标都是直线AB也就过点了.所以直线AB恒过定点

结论2：过椭圆的左顶点任意作两条互相垂直的直线交椭圆于另外两点A，B，则直线AB过定点

探究3：如图3，已知椭圆C的上顶点为E，过E有两条互相垂直的直线分别交椭圆于A，B两点，试问直线AB有什么特点？

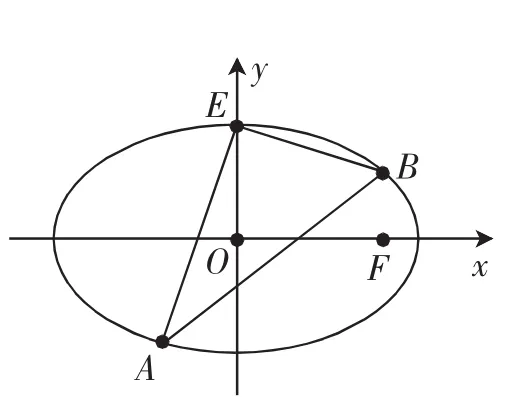
图3

解析：与如上探究2的解析类似，可以得到直线AB恒过定点

结论3：过椭圆的上顶点任意作两条互相垂直的直线交椭圆于另外两点A，B，则直线AB过定点

探究4：如图4，已知双曲线C的右顶点为E，过E有两条互相垂直的直线分别交双曲线于另外两点A，B，试问直线AB有什么特点？

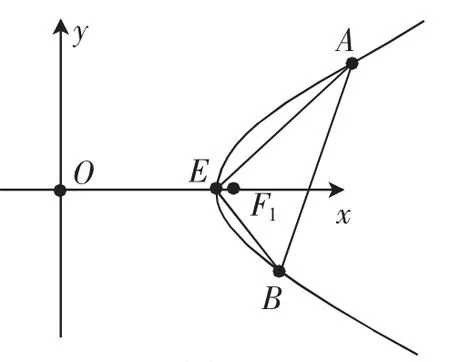
图4

解析：（限于篇幅本文仅考虑a>b的情形，左半支图形略）记直线EA的方程为y=k（x-a）（k≠0），联立方程消去y得到（a2k2-b2）x2-2a3k2x+a2（a2k2+b2）=0，从而有A以代替k，可以得到当k≠±1时，直线AB的斜率为所以直线AB的方程为即所以直线过点当k=±1时，A，B两点的横坐标都是直线AB也就过点了.故直线AB恒过定点

结论4：过双曲线的右顶点任意作两条互相垂直的直线交双曲线于另外两点A，B，则直线AB过定点

三、结论的拓展

细究如上探究过程，可以发现，如上结论的逆命题也成立.

拓展1：给定抛物线y2=2px，过点（2p，0）任意作直线交抛物线于另外两点A，B，则线段AB对顶点张直角.

拓展2：给定椭圆过点任意作直线交椭圆于另外两点A，B，则线段AB对左顶点张直角.

拓展3：给定椭圆过点任意作直线交椭圆于另外两点A，B，则线段AB对上顶点张直角.

拓展4：给定双曲线过点任意作直线交双曲线于另外两点A，B，则线段AB对右顶点张直角.

显然，由对称性，还可以发现其他的定点和直角.

四、结论运用——考题链接

例1（2013年安徽理）已知直线y=a交抛物线y=x2于A，B两点，若该抛物线上存在点C，使得∠ACB为直角，则a的取值范围为__________.

解析：由结论1、拓展1及对称性，可以发现，直线y=1交抛物线得到的A，B两点对顶点张直角，点C在顶点处就满足要求.由题意，只要直线y=1向上移动即可，所以a的取值范围为a≥1.

例2（无锡市2015届高三第一学期期末考试）如图5，已知椭圆C：的上顶点为A，直线l：y=kx+ m交椭圆于P，Q两点，设直线AP，AQ的斜率分别为k1，k2.

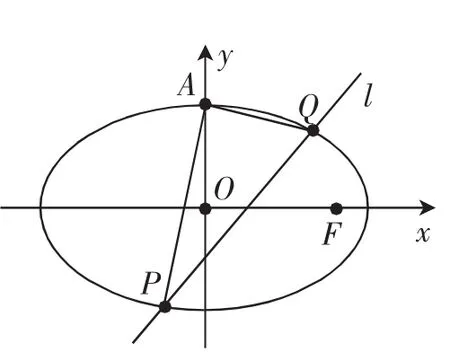
图5

（1）略；

（2）若k1k2=-1时，证明：直线l：y=kx+m过定点.

解析：k1k2=-1就表示直线AP，AQ互相垂直，由结论3，直线l必过定点

例3如图6，已知焦点在x轴上的椭圆C过点（0，1），且离心率为Q为椭圆C的左顶点.

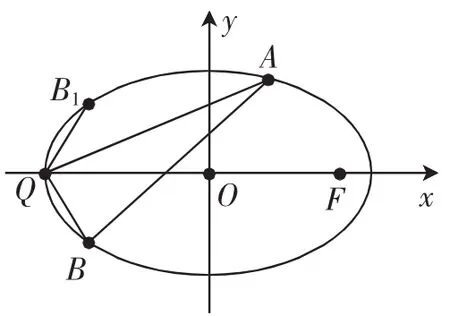
图6

（1）求椭圆C的标准方程；

解析：（1）易得

学生在上述自主探究的过程中，不仅仅是完成一个个结论，更是宝贵的生命历程，心智的参与过程，从而可使学生感知获取知识的不易与艰难.整个探究过程中思维的调控、优化，不仅是能力的提高，更是对学习信心的激发.

五、教学反思

波利亚说：“一个专心的认真备课的老师能够拿出一个有意义的但又不太复杂的题目，去帮助学生挖掘问题的各个方面，使得通过这道题，就像通过一道门户，把学生引入一个完整的数学邻域.”首先，学生的主观能动性得到发挥.让学生自己去研究问题，获得对知识的再发现，这本身就是获取知识的心路历程，要让学生知晓探究知识的过程是艰辛的，但是获取知识的结果是一件令人兴奋的事，同时也体现了对学生的教学不一定非要在课堂讲授，也可以是课外，教学和研究是相辅相成的，双方是充满互动的.教师在教学中可以在这方面多研究，多下功夫，这对学生的成长历程都是有帮助的.正如日本数学教育家米山国藏所说：“学生在学校所学的数学知识，毕业后若没什么机会去用，一两年后就会忘掉.然而，不管他从事什么工作，唯有深深铭刻在心中的数学的精神，数学的思维方法，研究方法，推理方法和看问题的着眼点等，却随时随地的发生作用，使他们受益终生.”通过研究性学习，使笔者深深意识到除做好日常教学外，可以多开展这样的研究性学习，使学生学中乐，乐中学，真正做到教学相长.

我们一线数学教师备课时要善于思考，善于联系，特别是课本上的习题，题目虽小，往往藏有大乾坤，通过教师的讲解，为学生做好知识铺垫，顺理成章地引导学生，使之达到会一题、通一类的目的，同时，也水到渠成地提升了教师本身的专业素养.