说课教学的案例示范——《数列概念与表示法》

☉江苏省南通市通州区金沙镇金沙中学 戴培红

说课教学的案例示范
——《数列概念与表示法》

☉江苏省南通市通州区金沙镇金沙中学 戴培红

说课是全新的一种教学模式，是考查教师课堂教学能力全面性和综合能力的一种较为全面的行为，也是观察、发现、思考教师教学行为的良好载体.说课与很多其他教学形式最大的差别在于，说课体现在“说”，这种“说”是头脑中知识处理转换为语言教学，以及和行为能力综合作用产生的，是极度体现教师教学设计、教学思考、教学行为、语言表述等综合能力的一种行为.

怎么说呢？说课是如何体现上述要求呢？笔者以一堂《数列的概念和表示方法》为例，简述说的准备、设计、过程和思考，恳请读者批评指正.

一、说教材

“数列的概念与简单表示法”是新课标必修5第二章第一节的教学内容.数列作为一种特殊函数，是函数学习的延续，也是反映自然规律的基本数学模型.本章通过生活实例引出数列的概念，把生活与数学有机地联系在一起，并介绍了数列的表示、等差数列、等比数列.数列在整个中学数学中，处于一个知识汇合点的地位.

教材根据学生的认知规律，按照“现实情境—数学模型—实际应用”的特点进行编写，由浅入深，突显数列的实际应用.针对上述分析，结合新课标的要求和高一学生的认知规律，我对本节课确定了如下三维教学目标、教学重点和难点

二、说目标

（1）知识与技能：理解数列的概念，了解数列是一种特殊的函数；掌握根据通项公式写出数列，根据数列前几项写出数列的通项公式.

（2）方法与过程：通过观察、类比、联想，自主建构数列概念和数列与函数的关系，领会类比的数学思想方法.

（3）情感态度与价值观：体验数学的科学价值和应用价值，培养善于观察、勇于探索的良好习惯和严谨的科学态度.

三、说重、难点

教学重点：理解数列概念，认识数列是反映自然规律的基本数学模型，掌握数列的通项公式表示法.

教学难点：（1）认识数列是一种特殊函数；（2）根据数列的前几项，归纳出数列可能的通项公式.

四、说过程

（创设情境，引出问题）

有人说：大自然是懂数学的.

情境1：树的生长与数学.

情境2：不坐飞船也能上月球.

教师：以上两个情境蕴涵着两列数：

年份 1 2 3 4 5 7 8……枝条数 1 2 3 5 8 13 21……

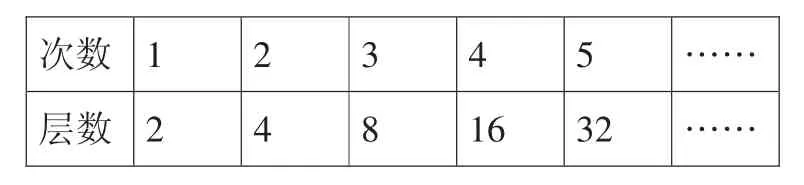
次数1 2 3 4 5 ……层数2 4 8 16 32 ……

设计意图：（1）用“树的生长”、典型的故事作为引入，让学生感受数列与生活、自然息息相关，激发同学们探求欲望；（2）对抽象出的一列列数，我采用表格的形式表示，主要考虑学生还没有建构数列概念，强化有序排列的特点.为自然引出数列概念，在此作好铺垫.

（观察归纳，形成概念）

由情境引出数列概念：按照一定顺序排列着的一列数叫做“数列”.

问题1：1，2，4，8，16，32与1，4，2，8，16，32是同一个数列吗？你认为数列的定义关键是什么？依据数列的定义，你还能挖掘出什么？（学生可能会从集合角度看数列，产生认知冲突）

教师：产生冲突原因在于“有没有顺序”，并对定义进行充分的挖掘.

设计意图：（1）产生“认知冲突”，领会概念的核心，区别于集合；（2）对定义进一步挖掘得出（首项、一般形式）等概念.

谜语：“赤橙黄绿青蓝紫”——猜一国家的名字.按照颜色顺序排成一列：以色列.

设计意图：概念建构后，强化定义的核心，同时活跃课堂气氛.

（数列的分类）

问题2：观察下面数列，各有什么特点？

（1）全体自然数构成的数列：0，1，2，3，4……

（2）目前通用的人民币面额按从大到小的顺序构成的数列：100，50，20，10，5，2，1，0.5，0.2，0.1，0.05，0.02，0.01；

（3）无穷多个3构成的数列：3，3，3，3……

（4）-1的1次幂，2次幂，3次幂，4次幂，…构成的数列：-1，1，-1，1……

（5）1996～2002年某市普通高中人数（万人）构成的数列：82，93，105，119，129，130，132.

教师引导，学生寻找.

学生归纳出数列的分类：按项数，可分为有穷数列和无穷数列；按项之间的大小关系（增减性）可分为递增数列、递减数列、常数列以及摆动数列（板书）.

设计意图：让学生对数列进行分类，自主建构知识，成为有效的知识，体现“发现法”教学的原则.

（认识数列与函数的关系）

互动游戏：请依据变化规律，在第3个小球内填入可能的数字，你是怎么想到的？那么第10个呢？有什么规律吗？

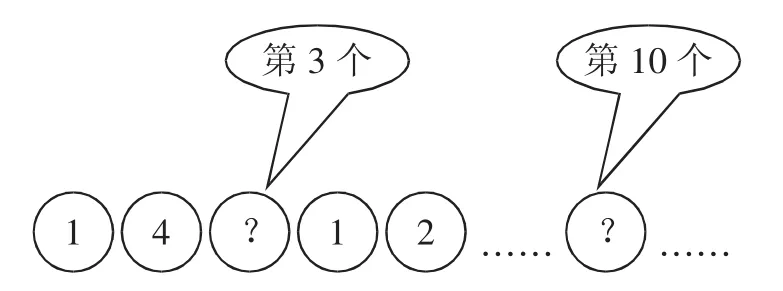
学生总结出规律（关系式）：an=n2.

教师总结：如果数列｛an｝的项与序号之间的关系可以用一个式子表示，这个公式叫数列的“通项公式”.

设计意图：（1）调动积极性、活跃气氛；（2）建构数列概念后，通过游戏让学生体验到有些数列的规律性，主动学习、建构知识，引出“通项公式”的概念，体现新课程学习知识螺旋上升的理念；（3）为“突破难点”作好铺垫.

问题3（探究）：数列：1，4，9，16，25，36，…序号与项之间的关系an=n2，请思考：这种关系是什么关系？你能联想到以前学过的哪些相关内容？

学生建构了通项公式概念后，形成了序号和通项的一一对应关系这样一个知识结构（如图）.学生看到右图，自然想到映射，而函数是特殊的映射，从而突破本课的难点“数列是特殊的函数”是水到渠成的事.当建构出“数列是特殊的函数”后自然对函数的定义域、值域、表达式、图像等性质进行探究.

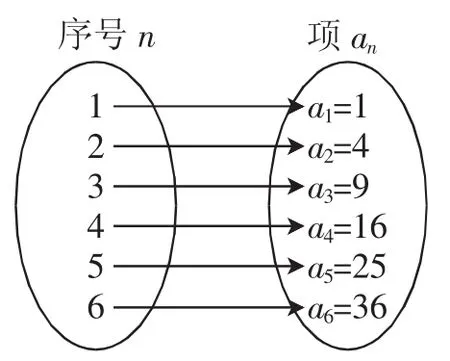
通过合作探究我们会得出一些数列作为特殊函数所具有的性质.

（应用巩固）

例1 根据下面数列的通项公式，写出前5项.

（1）an=n（n+1）；（2）an=（-1）n·n.

教师：引导学生只需令自变量n分别取1，2，3，4，5，代入即可.

设计意图：心理学认为，概念一旦形成，必须及时加以巩固，分梯度地设计了两个“互补型”的例题：例1是“由式给出数列”，加深学生对“通项公式可以看成数列的函数解析式”的理解.

例2 写出下面数列的一个通项公式，使它们前四项分别为：

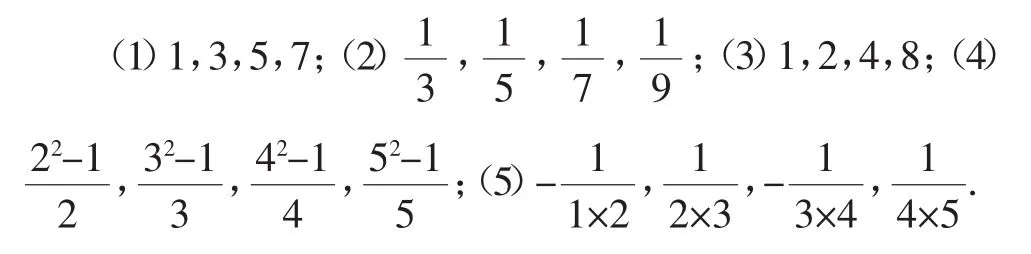
教师：引导学生找出自变量n与函数值an的关系式.

设计意图：例2是“由数给出数列的式”，分梯度设计了五个小题，从函数角度观察，归纳出通项公式，强化学生对“数列是一种特殊的函数”的理解.

（课内小结，课外探究）

（1）数列的有关概念；（2）数列的分类；（3）数列的通项公式；（4）数列与函数的关系.

设计意图：对本节所学的知识系统化、条理化，进一步巩固知识.

课外探究：“斐波那契（Fibonacci）”数列

大自然是懂数学的，数列：1，1，2，3，5，8，13……叫做“斐波那契（Fibonacci）”数列.动物、植物的生长受到这个数学规律的严格约束，这是动植物在大自然中长期适应和进化的结果，生物的繁衍生息离不开数学.在大自然中、在生活中，处处有数列的影子，只要你仔细观察、勇于探索，你就会发现它！

设计意图：（1）学习的途径不唯一，可以通过多种途径获得知识；（2）让不同的学生各获最佳发展；（3）培养勇于探索的情感态度和数学的应用意识，符合新课程的教学理念.

五、说思考

根据新课程理念和设计思路，本节课的教学方法侧重于“关注学习过程，改善学生的学习方式，让学生主动学习和建构知识”，心理学表明：所有的新知识只有通过学生自身的“再发现”活动，才能纳入其认知结构中，才可能成为下一个有效的知识.为更好地把握新课程理念和学生的认知规律，采用布鲁纳的“发现教学法”，本节课以问题为核心构建课堂教学，以问题核心，构建课堂教学，引导学生经历一个“再发现”的过程，在学习中，体现自主学习、合作学习、探究学习的新课程理念.

从说课来看，本课拥有完整的教学流程，从教材分析入手，说教学目标和重难点，主要是“说”清楚了教学的流程，从说的教学流程来看，坚持了以建构主义为基本理论指导的教学设计，体现学生在概念课教学中多学、多思、多实践，教师在教学中的多导、多引、多衔接.

总之，说课是一种全方位考查教师课堂教学能力的新模式，将教师教学中的所思、所想、所动均在“说”的过程中体现出来，思考这些设计在课堂教学中实施的可能性，将有助于教学的合理性和有效性.

1.李萍.说题教学的尝试［J］.数学通讯，2005（21）.

2.金秀青.“说题”——让数学课堂更精彩［J］.中学数学（上），2009（6）.

3.沈恒.说题，谈题，品题［J］.中学数学研究，2012（9）.