汽车座椅骨架的数值模态分析与验证

杨文彪，马迅，张继伟，张之江

（湖北汽车工业学院 汽车工程学院，湖北 十堰 442002）

汽车座椅骨架的数值模态分析与验证

杨文彪，马迅，张继伟，张之江

（湖北汽车工业学院 汽车工程学院，湖北 十堰 442002）

基于有限元软件Hyperworks建立某汽车座椅骨架的有限元模型，对其进行自由模态分析，得到骨架的固有频率及模态振型。通过模态试验验证了有限元模型的可靠性，研究了蛇形弹簧的模拟方式，发现蛇形弹簧的预紧力对座椅蛇形弹簧部分振动影响较大，为汽车座椅有限元模型的后续分析提供了仿真方法和理论依据。

汽车座椅；预紧力；蛇形弹簧；模态分析；固有频率

汽车座椅作为人体与车身的连接部分，对汽车的乘坐舒适性具有十分重要的影响。汽车座椅的舒适性由静态舒适性、动态舒适性和操作舒适性3个方面组成。汽车座椅的动态舒适性是指其传给人体的振动和冲击所能起到的缓冲及减震能力［1］，动态舒适程度由其结构的动态特性决定。汽车座椅骨架（Seat Frame）主要作用是支撑和连接座椅零部件，其由靠背骨架、坐垫骨架等组成。该座椅靠背骨架是管框式靠背骨架，坐垫骨架是半盆座结构［2］。本文中基于Hyperworks软件建立座椅骨架有限元模型，研究其动态特性，利用试验模态进行验证，获取相关的模态振型及固有频率，为座椅约束模态分析、静强度分析、静刚度分析打下了基础，为座椅骨架设计提供了参考价值。

1 基于有限元法模态分析

1.1 模态分析理论

模态分析有助于了解系统的振动特性，从整体上分析部件的振动情况。外界激励包括路面激励、发动机激励等通过轮胎、悬架、车身传递到座椅骨架，引起座椅骨架振动的响应都可以表示成由阻尼比、固有频率、振型等模态参数组成的各阶模态振型的叠加。如果上述外界激励的激振频率与座椅骨架的固有频率相近，就会引起共振，产生剧烈的振动，从而使座椅产生剧烈振动，加速座椅部件疲劳损坏，也会使汽车的乘坐舒适性降低［3］。

外界激励作用下座椅骨架的动力学方程为

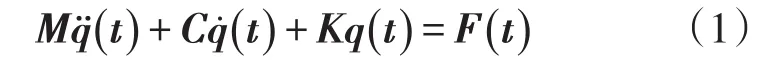
式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；F(t)外界振源对座椅的激励向量；̈(t)，̇(t)和q(t)分别为座椅振动的加速度、速度和位移向量。

模态分析是线性分析，基于有限元法进行模态分析一般忽略阻尼的影响［4］。自由模态是指在非零初始条件下部件的自由状态，即F=0系统不受外力，C=0忽略阻尼，自由模态分析能够反映出部件无约束理想状态状态下自身的固有频率以及与之对应的模态振型。自由模态的微分方程为

系统的特征值方程为

式中：wi为方程的特征值；φi为对应的特征向量。在座椅骨架的装配中，螺栓和靠背蛇形弹簧存在预紧力，使结构产生预应力，将预应力等效到座椅骨架部件上，座椅骨架局部刚度增大，其固有频率随之增加。

1.2 有限元建模

利用Hyperworks软件中Hypermesh模块建模，利用Optistruct模块进行自由模态分析。

座椅骨架爆炸图如图1所示，构件从几何角度分为3类：杆件结构、板壳结构、实体结构。将座椅骨架几何模型导入Hypermesh，对几何进行处理。板壳结构的简化即对几何模型抽取中面，去掉小的几何特征（比如说小的孔洞）、小的导圆、小的圆角。齿轮结构网格划分比较困难，所以实体结构的简化采用平滑的曲面替代，便于划分网格同时也能保证质量。杆件结构的简化即利用几何编辑，将杆件几何模型中轴线作出，便于1维单元的划分。几何模型简化完成后，将多余的一些拓扑线压缩掉，将多余的一些硬点去掉以保证网格划分的质量。

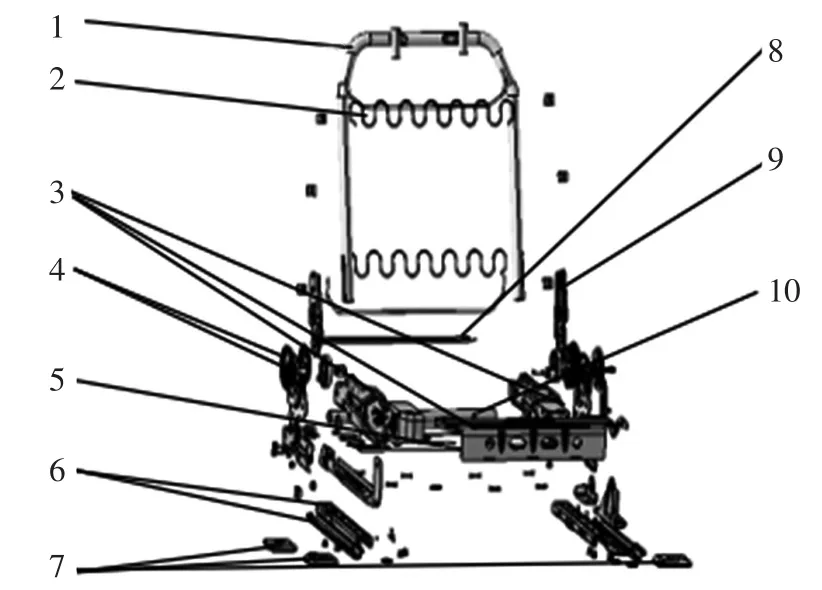
图1 座椅骨架爆炸图

板壳结构采用四边形单元和三角形单元混合划分，实体结构采用四面体单元划分，杆件结构以及螺栓采用梁单元划分，梁单元类型为CBEAM，基于铁木辛柯理论，采用刚性单元模拟焊点［5］。根据模型的几何特征确定单元尺寸，模型中壳单元的尺寸为3mm，四面体单元尺寸为2mm，梁单元的尺寸为3mm。图2为座椅骨架有限元模型。

图2 座椅骨架的有限元模型

有限元模型中四面体数量为70 302，四边形数量为35 114，三角形数量为977，梁单元数量为2853，刚性单元数量为411。三角形单元所占壳单元比例为2.7%。三角形单元刚度较大，所占比例不能超多10%［6］，网格质量要求控制如表1所示。在汽车行驶过程中座椅骨架在低频段容易引起共振，选取前9阶频率进行分析。有限元模态分析固有频率如表2所示，前9阶振型如图3所示。

表1 网格质量表

表2 有限元模态座椅骨架的固有频率分析结果

图3 自由模态分析前9阶振型

2 试验模态分析

试验模态分析是理论模态分析的逆过程。采用力锤法对座椅进行模态试验，激励信号由力锤敲击产生，响应点处由三向加速度传感器测量响应信号，从而获取系统的频响函数，由此建立频响函数矩阵；通过模态参数识别法，对拟合的频响函数曲线进行模态参数识别，估计结果并最终确定结构的模态参数。对于试验模态分析中，激励点的布置要考虑到能获取座椅骨架的模态振型，同时将激励点布置在容易敲击的位置，敲击质量的好坏直接影响试验的精度［7］。本次试验在座椅骨架上布置了32个激励点，点的位置如图4 a所示。座椅骨架由橡胶绳进行悬挂，如图4 b所示。利用米勒-贝姆PAK MKII数采采集试验数据，试验处理数据在LMS软件中进行，采用PolyMAX方法处理数据获取座椅骨架的固有频率以及相应的振型。为了避免信号迭混，采样频率设置为关心频率的2.56倍，本次设置为200 Hz。激励信号施加力窗，响应信号施加可调指数窗（加速信号的衰减，便于得到一个在此时间段末尾基本衰减为0的信号［7］）。每个点敲击次数设置为5次，相关性系数设置为0.8，以保证响应信号之间经平均之后存在着良好的线性关系［7］。将座椅骨架的自由模态试验获取的固有频率（表3）与有限元结果（表2）进行对比，有限元仿真与试验所得结果有一定偏差。

根据图3分析知4～9阶模态在有限元模态分析中所对应的振型为蛇形弹簧的振动，据此提出假设：未考虑蛇形弹簧的预紧力导致仿真结果偏差，座椅骨架中蛇形弹簧拆卸之后如图5所示。

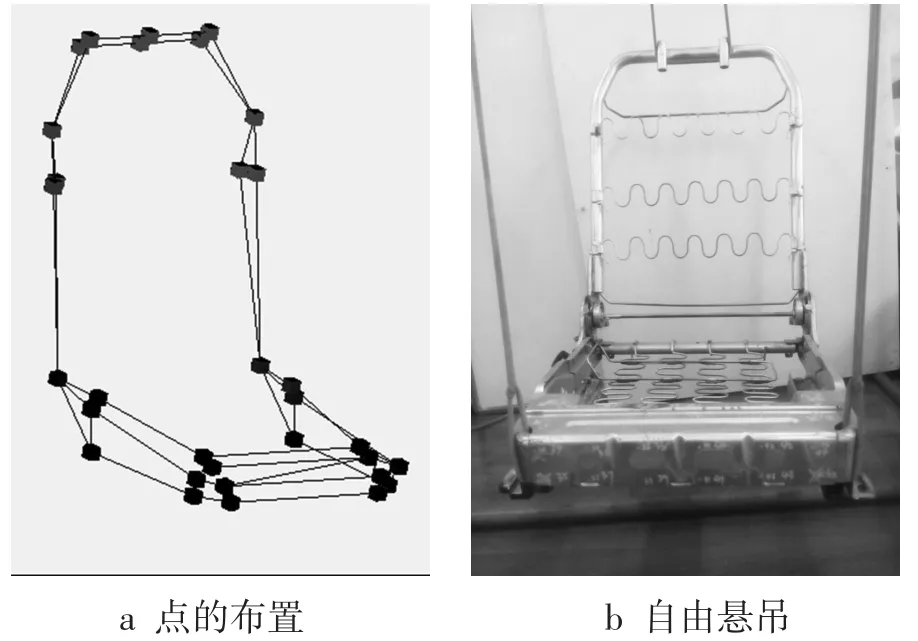
图4 座椅骨架点的布置及自由悬吊示意图

表3 模态试验座椅骨架的固有频率分析结果

图5 座椅靠背及坐垫处蛇形弹簧拆卸图

利用双杰系列管形测力计测量蛇形弹簧的预紧力，计算得到蛇形弹簧的刚度。对座椅蛇形弹簧的有限元仿真提出新的方案：利用Hypermorph对蛇形弹簧进行处理，使蛇形弹簧变为未装配之前的形状，如图6所示，靠背处蛇形弹簧b不变，a缩短37mm；坐垫处蛇形弹簧中间2个蛇形弹簧d不变、c缩短6mm，左右2个蛇形弹簧d不变、c缩短4mm，采用单个梁单元（便于施加预紧力）将其与座椅骨架连到一起，以所测轴向刚度为基准校核梁的材料参数。工况设置分为静力分析（施加预紧力）和模态分析（在静力分析的基础上）。新方案所得预应力模态结果如表4所示。

通过表4与表3对比可知，新方案是比较理想的处理方案，新方案与试验固有频率误差如表5所示。对新方案与模态试验的1～2阶振型进行对比，如图7所示。1阶振型为座椅骨架整体扭转，2阶振型为座椅滑轨总成左右反向振动。

图6 座椅靠背处及坐垫处蛇形弹簧尺寸

表4 预应力模态座椅骨架固有频率分析结果

表5 模态试验与新方案固有频率误差

图7 新方案与模态试验1～2阶振型对比

3 结论

蛇形弹簧的预紧力对座椅弹簧振动振型对应的固有频率影响较大，得到了蛇形弹簧的合适处理方式。考虑蛇形弹簧预紧力座椅骨架的有限元分析与实验结果更吻合，得到了可靠的有限元模型，验证了数值模态分析的可行性，获得了座椅骨架准确的模态参数，为汽车座椅的后续分析提供了仿真方法和理论依据。

［1］温吾凡.汽车人体工程学［M］.长春：吉林科学技术出版社，1991.

［2］钟柳华，孟正华，练朝春，等.汽车座椅设计与制造［M］.北京：国防工业出版社，2015：12-17.

［3］马迅，赵幼平.轻型客车车身结构刚度与模态的有限元分析［J］.湖北汽车工业学院学报，2002（1）：86-88.

［4］尹长城，马迅，陈哲.基于ANSYS Workbench传动轴的模态分析［J］.湖北汽车工业学院学报，2013，27（1）：15-17+22.

［5］王钰栋，金磊，洪清泉，等.HyperMesh&HyperView应用技巧与高级实例［M］.北京：机械工业出版社，2012.

［6］朱茂桃，智淑亚，王良模，等.汽车车身现代设计［M］.北京：国防工业出版社2014.

［7］沃德·海伦，斯蒂芬·拉门兹，菲尔·萨斯.模态分析理论与试验［M］.白话同，郭继忠，译.北京：北京理工大学出版社，2001.

Numerical Modal Analysis and Verification of Automobile Seat Frame

Yang Wenbiao,Ma Xun,Zhang Jiwei,Zhang Zhijiang
（School of Automotive Engineering,Hubei University of Automotive Technology,Shiyan 442002,China）

The finite element model of a car seat frame was established by the Finite element software HyperWorks.Then,the seat frame was analyzed through the free modal,the natural frequencies and the modal shapes were obtained.The reliability of the finite element model was validated by the modal test and the simulation of the serpentine spring was researched.It is found the effect of the serpentine spring preload on the seat serpentine spring vibration type is large.It provides the simulation method and the theoretical basis for the subsequent analysis of the finite element model of the car seat.

car seat;preload;serpentine spring;modal analysis;natural frequency

U463.83+6

：A

：1008-5483（2016）04-0005-04

10.3969/j.issn.1008-5483.2016.04.002

2016-07-06

湖北省重点实验室开放基金项目（ZDK1201307）

杨文彪（1990-），男，山东聊城人，硕士生，从事汽车有限元分析和振动方面的研究。E-mail：906568693@qq.com