基于Matlab的机械手运动学分析与仿真

陈洋，管殿柱

（青岛大学 机电学院，山东 青岛 266071）

基于Matlab的机械手运动学分析与仿真

陈洋，管殿柱

（青岛大学 机电学院，山东 青岛 266071）

在Solidworks中对上下料机械手进行三维建模，运用Craig版本的D-H法来描述机器人的连杆参数和关节变量，运用代数法求解出其运动学方程，在Marlab Robotics Toolbox中运用Link函数对其建模，并对其进行正向和逆向运动学仿真，从而验证数学方程的正确性。选取一小段路径对其进行轨迹规划，得出机械手末端执行器的空间轨迹以及各关节连续平稳的位移、速度和加速度曲线，延长了机器人的使用寿命，为机械手后期的动力学分析和控制研究提供了一定的理论基础。

上下料机械手；运动学分析；Robotics Toolbox；仿真

工业机器人系统主要由机械系统、传感系统、控制系统及信息处理系统组成，具有较高的耦合性和一定的复杂性［1］。因此工业机器人的机械系统部分应该与其他系统的设计相匹配，可以说是机器人系统的基础硬件部分，其机械系统的准确设计显得尤其重要。机械手作为高复杂性、高耦合性的机械系统，要让执行机构完成预定的轨迹和任务，需要对其在空间位置和姿态进行分析，从而进一步分析其位移、速度和加速度。而机器人运动学是从机构和几何的角度来描述和研究机器人的运动特性，而不考虑引起这些力或者力矩的作用［2］。

Matlab Robotics Toolbox是由澳大利亚科学家Peter Corke开发和维护的一种基于Matlab的机器人学工具箱，当前最新版本为第9版。该工具箱通过下载安装后可以在Matlab环境中运行，是专门用来解决机器人建模、运动学分析和轨迹规划问题的可视化软件，用户可以使用对应的命令来建模和分析。Matlab Robotics Toolbox通过内部定义的各种函数将机器人复杂的运动学问题变得高效、准确。同时，它能对机器人进行图形仿真，并能分析真实机器人控制时的实验数据结果，因而非常适合机器人学的教学和研究［3］。本部分选用该工具箱对上下料机械手进行分析和仿真。

1 上下料机械手的建模

1.1 上下料机械手的三维建模

本文中研究的上下料机械手的机械本体结构主要由基座、腰部、大臂、小臂和末端执行器等组成。它具有4个自由度，均为旋转关节，且每个旋转关节处都配置一个合适的电机和减速器来增大力矩，使其满足实际的力矩要求。其中基座为机器人最底部的支撑和各种接线部分，需要一定的强度和刚度要求。腰部也是机器人的支撑元件之一，通过电机和减速器驱动使其相对于基座绕着z轴旋转，从而实现机械手水平面的各个转角的变化。大臂作为连接腰部和小臂的部分，起着传递力和力矩的作用。小臂和末端执行器夹手更加灵活了机械手的工作空间，使得该机械手能完全满足滚丝工艺的各种前伸、抓料、放料、返回等指令动作，从而完成该滚丝机的上下料过程。各个关节间使用轴承、弹性挡圈和转轴连接，从而在满足一定精度的要求下，降低惯性力和力矩带来的振动，使得机器人的运动过程更加平稳。根据上述设计准则，运用Solidworks对机器人进行建模，如图1所示。

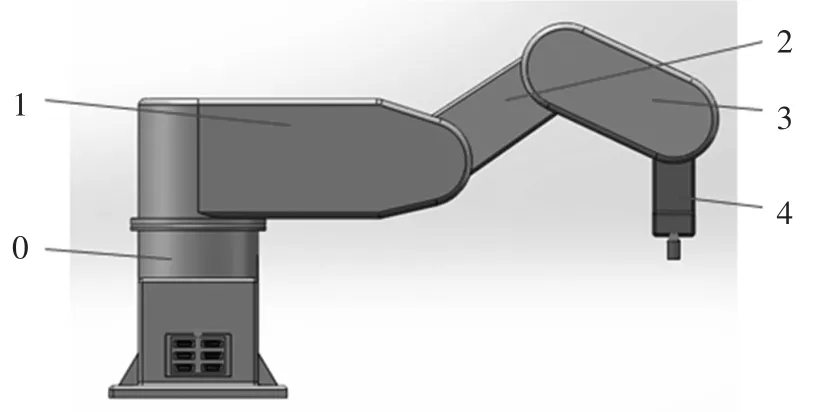
图1 机械手三维模型图

1.2 机械手的Matlab建模

根据图1中三维模型图，可以绘制出其D-H坐标系的示意图，如图2所示。由于该机械手为四自由度关节型机器人，其关节变量为各关节旋转角，其初始值θ1为0°、θ2为35°、θ3为-60°、θ4为 25°，其余3个参数为常量。对图2的连杆参数和关节变量分别进行测量，即a1为383.92mm、a2为280mm、a3为200mm、d2为-165mm、d3为165mm，结果如表1所示。

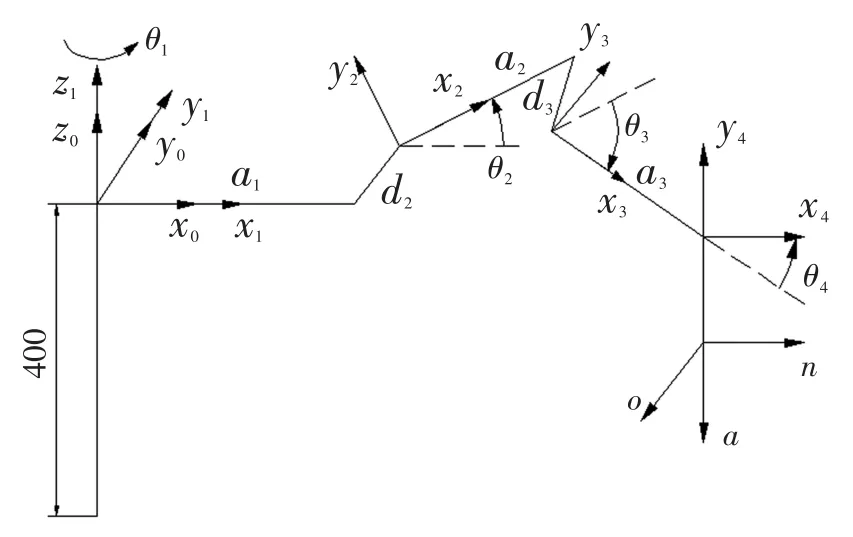
图2 D-H坐标系的示意图

表1 机械手连杆参数和关节变量值

在Robotics Toolbox中，将机械手各关节简化为一系列杆件，运用Link函数可以建立直观的机械手模型。Link函数的一般形式如下［4］：

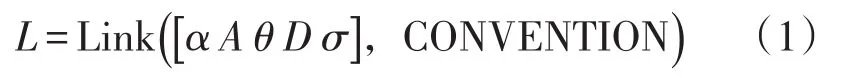
式中：L为关节名称；α为连杆扭角；A为连杆长度；θ为关节转角；D为连杆偏距；σ为关节类型：0代表旋转关节，非0代表移动关节。而参数CON⁃VENTION分为standard和modified，其中standard表示采用标准的D-H参数，而modified表示采用改进的D-H参数。考虑到前面采用的是Craig版本的D-H法，该方法与标准的D-H法的区别是前者每一杆件的坐标系z轴和原点固连在该杆件的前一轴线上。显然此处选择的是CONVENTION类型为modified，Matlab程序如下：

在Robotics Toolbox工具箱中定义机器人的DH参数，用plot函数绘制出机器人的三维空间模型，从而方便直观地了解机器人的运动特性，如图3～4所示。图3为机器人控制面板，它是通过改变关节变量运用drivebot函数来驱动机器人关节的运动，即每个关节都有一个对应的关节变量滑块，图中的q1，q2，q3和q4分别表示机器人的4个对应关节角θ1，θ2，θ3和θ4，可以拖动滑块或者在其后空白处输入某个关节变量值即可使图4中的机器人进行相应地运动，从而完成一定的作业要求。从图4可以看出，该机器人模型具有4个自由度，在每个关节处都有一条虚线表示关节轴线，从而有利于反应机器人的运动情况［5］。

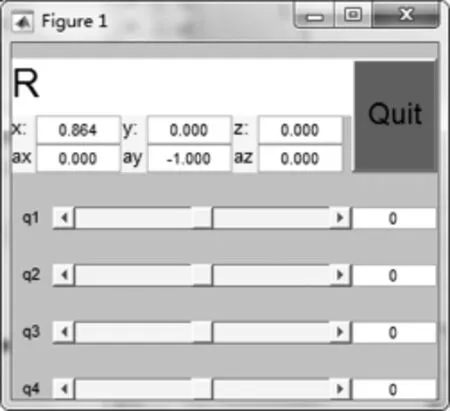
图3 机器人控制面板

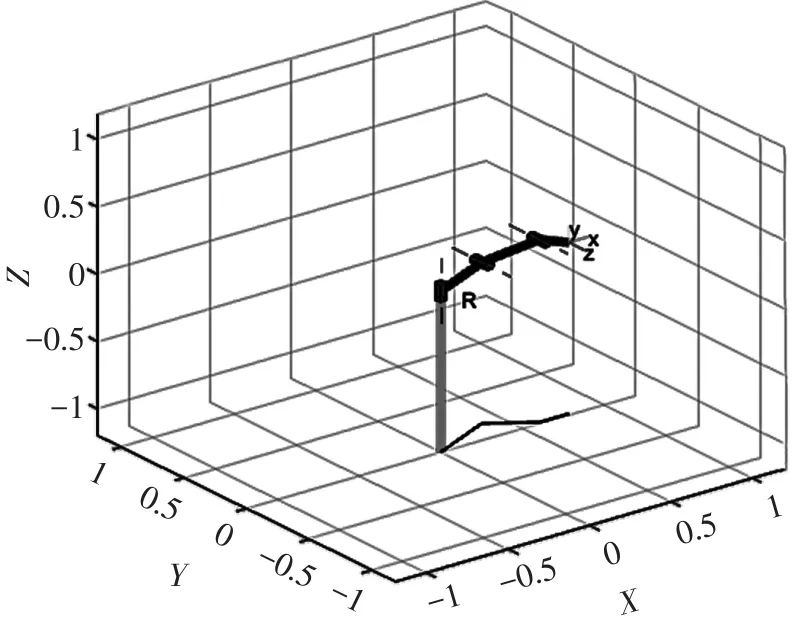
图4 机器人三维空间模型

2 机械手正运动学分析与仿真

运用代入数值的方法对正运动学方程进行了初步的检验，考虑到其矩阵计算的复杂性，也可以运用Robotics Toolbox工具箱对其动态验证来进一步确定该正运动学方程的正确性。验证正运动学方程正确性的流程图如图5所示。

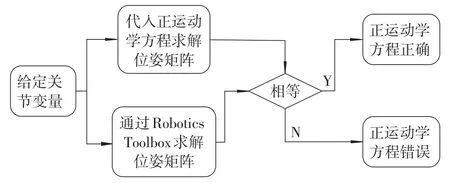
图5 验证正运动学方程流程图

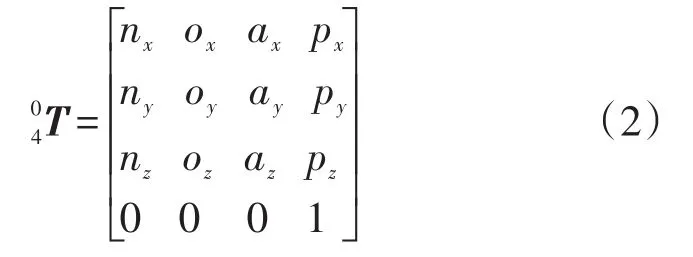
矩阵中各元素各字母的值分别为

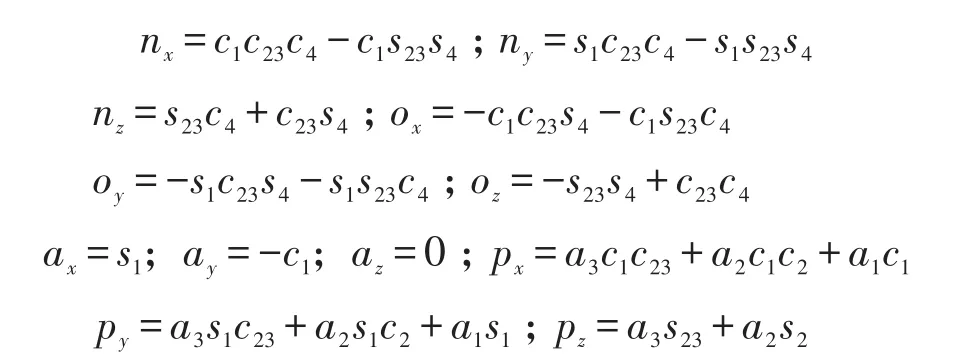
式中：s1代表 sinθ1；c1代表 cosθ1；s23代表sin(θ1+θ2)；c23代表cos(θ1+θ2)。以此类推。

在Robotics Toolbox中进行正向运动学仿真的函数为fkine函数［7］，该函数可以输入已知的关节变量来计算出其对应的位姿，其调用格式为

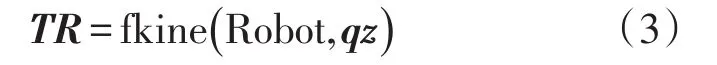
式中：qz表示某个状态下机器人的关节变量矩阵；Robot表示该机器人的名称；TR表示通过qz定义的该机器人正向运动学的解，它是指对应于qz各关节变量时末端的位姿矩阵。

取机器人最危险的工作状态来进行仿真，即取qz=[ ]

0,0,0 ,π/2，在Matlab中通过式（2）可求出其对应的末端位姿矩阵，其结果为

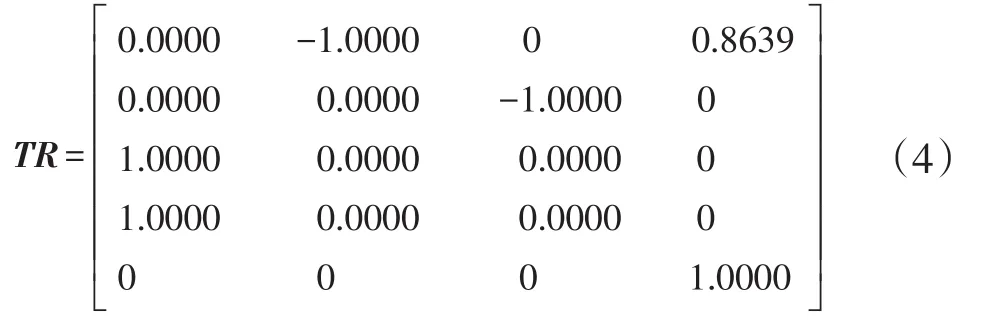
3 机械手逆运动学分析与仿真

机器人逆向运动学问题与正向运动学问题相反，是通过给定的末端手爪位姿来确定各个关节变量，从而实现机器人的控制［8］。可以说，逆向运动学问题在实际中运用更多，但由于其解的不确定性，逆向运动学问题变得更复杂。同正向运动学问题一样，可以运用Robotics Toolbox工具箱对其动态验证来进一步确定该逆运动学方程的正确性。验证逆运动学方程正确性的流程图如图6所示。

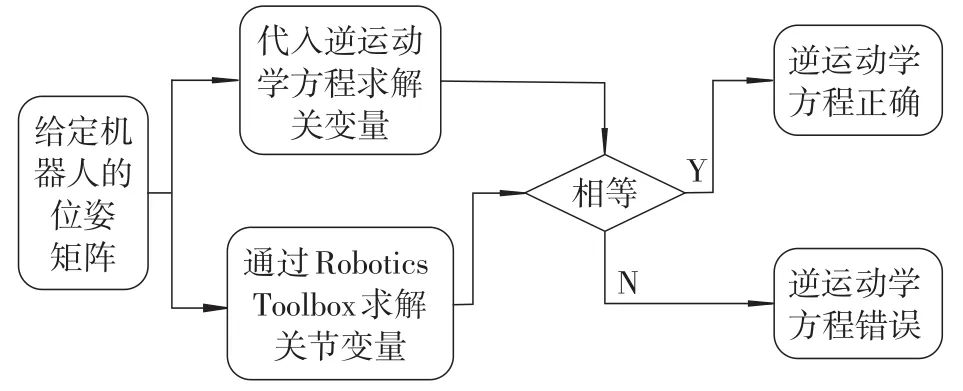
图6 验证逆运动学方程流程图

1）求解θ1对式两边同时左乘得，根据等式两边矩阵元素（2，4）对应相等，得

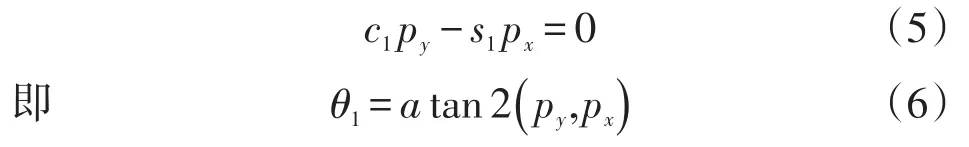
式（6）中，θ1运用双变量反正切函数来求解，该函数提供2个自变量y和x，其精度适用于整个定义域。

2）求解θ2对式两边同时左乘得，根据等式两边矩阵元素（1, 4）和（2,4）分别相等，得

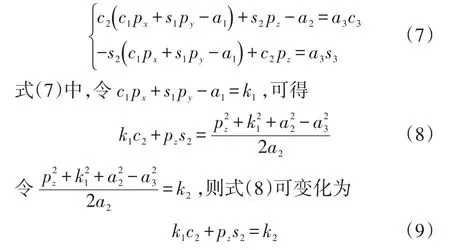
运用数学中三角代换：

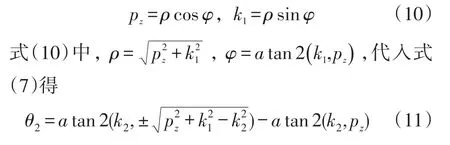
式（11）中，正负号表示θ2有2个满足条件的解。

3）求解θ3由式（7）中两式相除得：

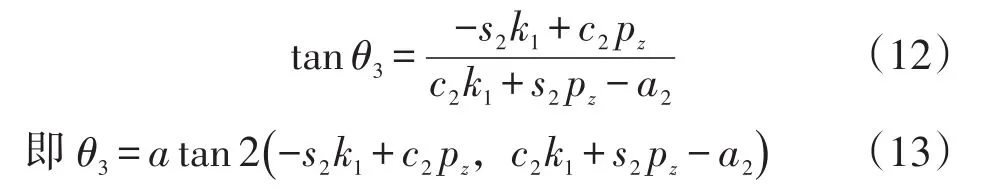
4）求解θ4考虑到坯料在轨迹的关键点处需处于竖直状态，则其转动角度之间存在以下关系：

故最终的θ4为

在Robotics Toolbox中运用ikine函数对机器人进行逆向运动学问题仿真，该函数通过输入末端位姿矩阵来求解对应的关节变量，注意到机器人逆向运动学问题解的不唯一性，因此得出的解可能与之前不同。ikine函数的调用格式为

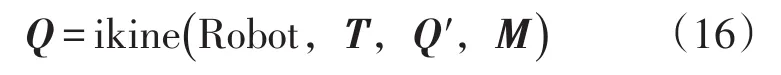
式中：Robot表示该机器人的名称；T表示末端的位姿矩阵；Q′为初始的猜测点；Q为对应于T的关节变量值。若机器人的自由度数目小于6时，则需要利用M来忽略某个关节自由度，考虑到本文中机械手自由度为4，故此时M=[1 1 1 1 0 0]。取机器人在危险工况来仿真求逆解，此时T取式（4）中的TR矩阵，在Matlab中通过式（5）求出逆解：

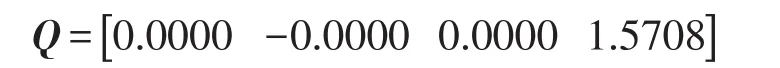
由于Robotics Toolbox求逆解过程中与初始猜测点有关，故可以多次改变猜测点的形式来求出所有的逆解。前面的正、逆运动学方程均是通过人工代数法一步步计算得到最后的位姿矩阵或者关节变量，而Robotics Toolbox则是通过调用其内部函数对其建模和仿真求解，那么人工求解的结果与仿真结果相同就验证了其正确性。

4 上下料机械手轨迹的仿真

在Robotics Toolbox中进行轨迹规划是运用的ctraj、jtraj和trinterp函数，它们分别对应不同的规划方法：笛卡尔规划、关节空间规划和变换插值规划［9］。笛卡尔规划较为简单，它是以机器人的关节变量的函数来进行描述轨迹，而笛卡尔规划虽能直观地看到空间中轨迹，但是计算量大，较为复杂。本文中选用jtraj函数来对机器人进行关节空间轨迹规划，其调用格式为

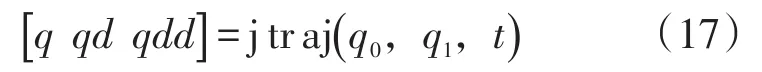
式中：q表示从状态q0到q1的关节空间轨迹规划；t表示给定的运动时间；qd和qdd则可以返回轨迹规划过程中的速度和加速度值。

在上下料机械手关节空间的插值计算中，其运动路径点一般是用工具坐标系{}T相对于工作坐标系{}

S的位姿来表示。首先在求得逆运动学方程的基础上，将一系列关键点坐标转换成关节角度的矢量值，然后对每个关节用某个函数去拟合，使该函数依次经过所需的关键点，从而完成实际工作任务。此外，在对其进行插值时需要考虑很多约束条件：抓取物体时，机器人末端的初始点、提升点、下放点和停止点等各关键点上的位姿、速度和加速度的要求；整个时间段内，各个关节位移、速度和加速度甚至是脉动（二次加速度也称冲击）的连续性要求；关节变量的极值在实际的变化范围内等。

选取机器人末端初始点A（0.795,0,0.076）到机器人取料的毛坯位置点B（0.871，-0.163，-0.187）这一小段进行轨迹规划。首先分别用ikine函数求出A、B点的逆解，然后在Matlab中运用式（17）对机械手末端从A点到B点进行轨迹规划，Matlab主要程序如下：

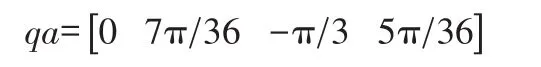
%机器人末端在A点时的关节变量值

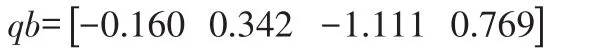
%机器人末端在B点时的关节变量值

在Matlab中输入上述程序后可得机器人的末端手爪空间轨迹和各杆件的位移、速度和加速度曲线，如图7～8所示。

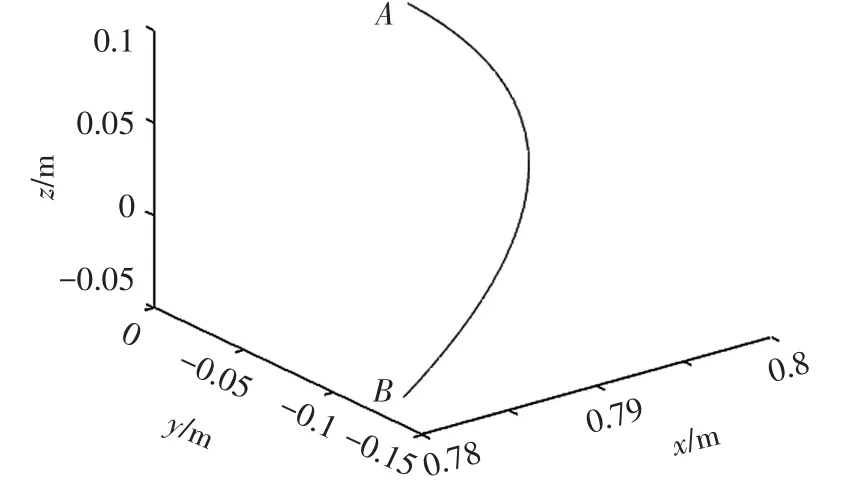
图7 机器人末端手爪轨迹图

由图7中A、B坐标可知：机器人末端手爪能完成从A点运动到B点的任务，且满足机器人运动的平滑性要求，即机械手各关节位移、速度和加速度曲线均是连续光滑的曲线。由图8可以看出：随着时间的变化，各个关节的角位移、角速度和角加速度曲线均是连续平稳地变化，使得电机在运行时，各关节之间的冲击较小，从而增强了机器人的平稳性，这在机器人的轨迹规划中显得尤为重要。

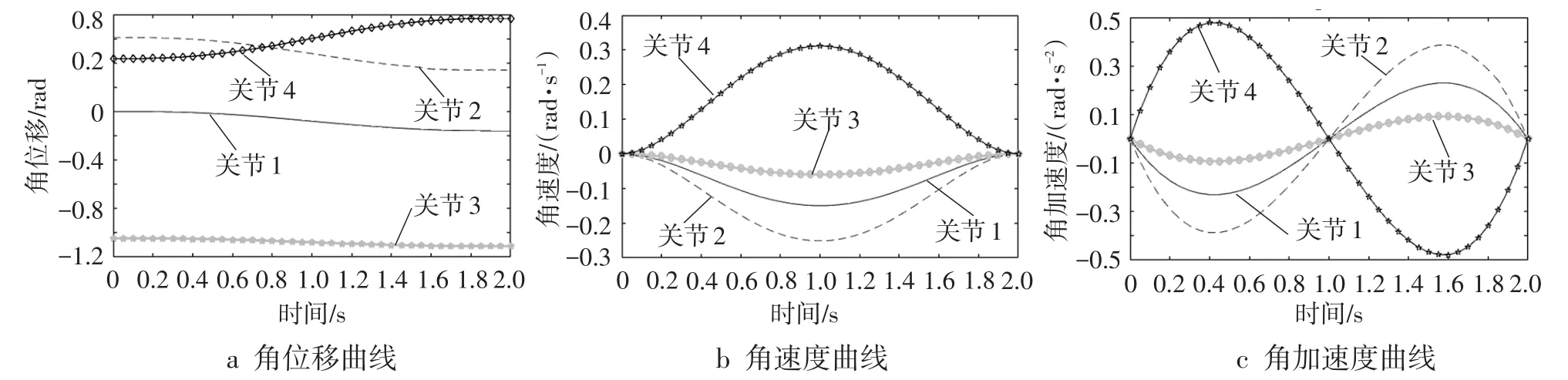
图8 机器人各关节角位移、角速度和角加速度曲线图

5 小结

本文中运用Craig版本D-H法求解机器人正运动学方程，然后运用Matlab中Robotics Toolbox工具箱建立机器人杆件三维模型，并对其进行正、逆运动学仿真，从而进一步验证了前者数学方程的正确性。选取了一段路径对其进行轨迹规划，得出其各连杆连续平滑的角位移、角速度和角加速度曲线，为后期机器人动力学分析和控制奠定了基础。

［1］蔡自兴.机器人学［M］.北京：清华大学出版社，2000.

［2］李延富.CINCINNATI机器人运动学和动力学的研究与仿真分析［D］.沈阳：东北大学，2005.

［3］吴伟国，赵洋.仿人四指灵巧手的抓持能力分析［J］.机械设计与制造，2010（4）：188-190.

［4］赵小英，梅志千.双臂教学机器人的运动分析及仿真［J］.河南大学常州分校学报，2006，20（1）：24-27．

［5］CRAIG J J.Introduction to robotics［M］.New York:Ad⁃dision-Wesley Publishing Company，2006.

［6］殷际英，何立婷.HP6机器人运动学动力学分析及运动仿真研究［J］.机械设计与制造，2009（3）：189-191.

［7］赵献丹，何庆中，刘明，等.基于MATLAB的微电驱串联机械手工作空间域解算与仿真［J］.四川理工学院学报，2006，19（5）：5-8.

［8］Zhao Qingjie，Sun Zengqi．Image-based Robot Motion Simulation［J］.Optics Communications，2002，205（4-6）：257-263.

［9］孙增圻.机器人系统仿真及应用［J］.系统仿真学报，1995，7（3）：23-29．

Kinematic Analysis and Simulation of Robot Based on Matlab

Chen Yang,Guan Dianzhu
（College of Mechatronics Engineering,Qingdao University,Qingdao 266071，China）

The three-dimensional modeling of the loading and unloading robot was carried out in Solid⁃works,the link parameters and joint variables of the robot was described by the D-H method of Craig version,and the kinematic equation was obtained by the algebraic method.The robot was modeled by the Link function in Matlab Robotics Toolbox,then the forward and inverse kinematics of the robot was simulated to verify the correctness of the mathematical equations.A short path was selected to do the trajectory planning,and the space trajectory of the manipulator end-effector,continuous and smooth displacement,velocity and acceleration curves of each joint was obtained.It prolongs the service life of the robot,and provides theoretical basis for the later dynamics analysis and control research.

loading and unloading robot;kinematic analysis;Robotics Toolbox;simulation

TP242

：A

：1008-5483（2016）04-0047-05

10.3969/j.issn.1008-5483.2016.04.011

2016-07-04

陈洋（1992-），男，湖北孝感人，硕士生，从事数字化设计及虚拟样机技术研究。E-mail：1451382965@qq.com

管殿柱（1969-），男，山东青岛人，副教授，主要从事数字化设计及虚拟样机技术研究。E-mail：gdz_zero@126.com