夹层结构中夹层声场的处理方法研究

宁少武， 史治宇

(南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016)

夹层结构中夹层声场的处理方法研究

宁少武， 史治宇

(南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016)

以二维双层弹性梁为例研究夹层声场的处理方法，从不同的物理视角，提出了夹层结构中夹层声场的横向声模态展开方法和声波导模态展开方法，并与夹层声场采用结构模态展开形式和声腔纯模态展开形式时的传声性能作对比。运用四种夹层处理方法计算了不同参数组合形式结构的传声损失。计算表明：夹层的横向声模态函数展开方法与结构模态展开方法在计算结构传声损失上是等价的；声波导模态函数展开方法在计算结构传声损失上与声腔模态展开方法是等价的；结构的传声损失曲线中的隔声低谷由结构共振、‘梁-空气-梁’共振以及驻波共振共同作用产生的结果；四种计算方法可以反映结构共振、‘梁-空气-梁’共振以及垂直与结构表面方向的驻波共振对结构传声损失的影响，除此而外，夹层的声模态展开形式和声波导模态展开还反映了平行于结构表面方向的驻波共振和其余的声模态对结构隔声性能的影响，因此在其对应的传声损失曲线中有更多的隔声低谷。

夹层板结构;结构模态;声模态;声波导模态;共振频率

夹层结构具有优良的声学性能，在高速列车、舰船潜艇以及航空航天等领域有广泛的应用，针对夹层结构的声振耦合特性已进行了广泛的研究。以双板空腔结构为例，早期对双板空腔结构的声振耦合特性研究通常简化为无限大结构，未有考虑结构边界条件的影响。ANTONIO等[1]理论研究了无限大双板空腔建筑隔墙结构的隔声性能；KROPP等[2]对双板结构在低频段隔声性能开展了优化设计方面的研究；LONDON[3]基于单板声阻抗发展了无限大双层板腔结构对混响入射声波的理论模型。对于有限大的夹层结构必须考虑结构的边界条件对结构声振耦合特性的影响，VILLOT等[4]在无限大结构理论的基础上发展了平面波空间窗截断的方法近似模拟有限大边界条件的影响；卢天健等[5]分别建立了简支和固支两种边界条件下双板空腔结构传声理论模型，研究讨论了一系列系统参数对结构传声特性的影响。

对于有限大的夹层结构，不仅结构的边界条件对结构本身的声振耦合特性有影响，夹层结构中夹层声场的边界条件对结构传声损失影响也很显著。然而，对夹层声场的表示通常采用两类表示方法：①采用空腔模态展开的方法表示夹层声场的声压分布，其假设夹层声场为刚性边界。例如，CHEN 等[6]采用空腔模态展开的方法计算分析了声激励与机械激励条件下声介质与连接结构两种途径对矩形声腔内部声场的影响。②从波动观点出发将中间声场表示为结构模态函数的级数形式，其认为中间声场声压分布与结构模态函数形式相同。例如，XIN等[7]采用结构模态函数展开方法对简支双板空腔结构的声振耦合特性进行了理论研究。

从声场的角度，考虑夹层边界的影响，提出两种夹层声场处理方法：①假设声场在平行于结构表面方向形成驻波声场，而垂直与结构表面方向的波数与入射声场相同，即横向声模态展开方法；②将空气夹层看作声波导，提出采用声波导的模态函数展开方法表示夹层结构的中间声场。为了简化分析，以二维双层弹性梁为计算模型，分别采用结构模态函数展开法、空腔模态展开法以及本文提出的横向声模态展开方法和声波导模态展开方法来研究二维双层弹性梁的声振耦合特性，讨论夹层声场边界条件对结构传声损失的影响。以二维双层弹性梁为计算模型，对于三维声场，相比之下，处理方法相同，只是计算过程较为复杂。

1 结构的振动控制方程和声学波动方程

如图1所示，平行的两弹性梁简支安装在刚性声障上，长度为a;上下弹性梁的厚度分别为t1和t2;截面积分别为A1和A2。弹性梁将声场分为入射声场1、中间声场2和辐射声场3;在中间声场2的厚度为b;入射声波的入射角为θ。平面简谐入射声波的声压速度势为

φ=Ie-j(kxx+kzz-ωt)

(1)

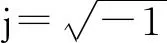
kx=k0sinθ

(2a)

kz=k0cosθ

(2b)

式中:k0=ω/c0为空气中声波的波数;c0为空气中声波的传播速度。

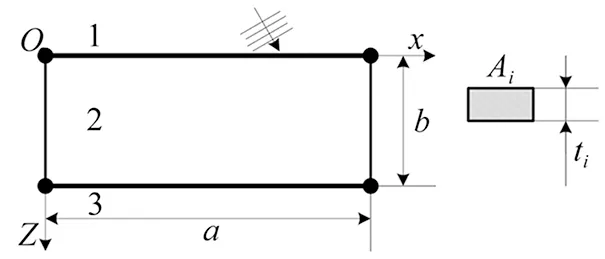
图1 夹层结构示意图

在简谐平面入射声波的激励下，双层弹性梁的振动控制方程和声场控制方程分别为

(3)

(4)

(5)

pi=jωρ0Φi

式中:D1和D2分别为上下两弹性简支梁的弯曲刚度；w1和w2分别为上下两弹性简支梁的横向振动位移；ρ1和ρ2分别为上下两弹性简支梁的材料密度；Φ1，Φ2和Φ3分别为入射声场1、夹层声场2和辐射声场3的速度势函数;pi为相应的声场声压；ω为角频率;ρ0为空气的密度。

对于简支边界条件，则梁在边界处的横向位移和弯矩都应该等于零，即

(6)

在结构与声场的流固界面上满足法向速度连续条件，即速度连续条件

(7)

(8)

(9)

(10)

2 夹层结构的声振耦合特性求解

为了研究夹层声场的边界对结构传声损失的影响，对于夹层声场的速度势函数Φ2，基于不同的物理含义，采用四种不同的表示方法，即结构模态函数展开方法、声腔模态展开方法、夹层的横向声模态函数展开方法和声波导的模态函数展开方法，其速度势函数分别表示为Φs,2、Φa,2、Φg,2和Φw,2。

2.1 方法1：采用结构模态函数展开方法

弹性梁为简支支撑，则其振动位移可以表示成简支模态函数的形式

(11)

(12)

式中:M为结构模态的阶数;α1,m和α2,m分别为上、下两弹性梁的振动模态系数，φm(x)为简支模态函数，

简支弹性梁的刚性声障约束密封腔内的空气，使得空腔内平行于弹性梁的声压分布与梁简支模态函数的级数形式相同，因此声压速度势函数可以表示为

(13)

(14)

(15)

式中:kz为声场中z向波数分量；Im、εs,m和ξm分别为入射声场1、中间声场2和辐射声场3中正行波的幅值；βm和ζs,m分别为入射声场1和中间声场2中负行波的幅值。入射波幅值Im由入射声波的声压速度势φ得到

将式(11)～式(15)代入边界条件式(7)～式(10)，联立求解，可得

将式(11)～式(15)代入式(3)和式(4)中，利用简支模态函数的正交性，整理可得

(16)

式中:

通过上述计算求解，可以得到上下两弹性梁的振动模态系数α1,m和α2,m，从而求得βm、εs,m、ζs,m和ξm的值。

2.2 方法2：采用声腔模态展开方法[8]

假设夹层空腔为刚性封闭空腔，夹层声场的速度势函数采用空腔的声模态表示为

(17)

(18)

式中:K和L分别为声模态x轴方向和z轴方向的声腔模态阶数;且声模态ψkl(x,z)满足

(19)

由格林公式有

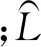
(20)

式中:

由振动模态函数的正交性，由方程(3)和(4)可以得到

(21)

(22)

式中:

Λ1,kl,m，Λ2,kl,m，Γ1,kl,n和Γ2,kl,n为声腔模态与结构振动模态之间的耦合系数；将式(20)代入式(21)～式(22)，整理可以得到

通过上述计算求解，可以得到上下两弹性梁的振动模态系数α1,m和α2,m，从而求得βm、μa,kl和ξm的值。对于声学刚性边界假设，ψkl(x,z)选为

2.3 方法3：采用夹层的横向声模态函数展开方法

对于夹层声场的分布情况，若假设在x轴方向形成驻波声场，同时波数满足式(2.b)，则夹层的声压速度势函数可以表示为

(23)

式中:N为声波导模态的阶数；εg,m和ζg,n分别为中间声场2中正行波和负行波的幅值；φg,n(x)为夹层声场在x轴方向的声模态函数。声压速度势函数Φg,2(x,z;t)同样满足边界条件(8)和(9)，代入可得

(24)

(25)

式中:

由振动模态函数的正交性，由方程(3)和(4)可以得到

(26)

(27)

式中:

Λmn、Γ1,nk和Γ2,nk为声腔模态与结构振动模态之间的耦合系数；将式(24)～式(25)代入式(26)～式(27)，整理得到

通过上述计算求解，可以得到上下两弹性梁的振动模态系数α1,m和α2,m，从而求得βm、εg,n、ζg,n和ξm的值。其中φg,n(x)按照声腔边界条件来选取。当边界为刚性边界和绝对软边界时，φg,n(x)分别可以选取为

2.4 方法4：采用夹层的声波导模态函数展开方法

若将夹层声场假设为波导，采用波导的模态展开形式表示空腔内声压速度势函数为

(28)

式中:x轴方向和z轴方向的波数满足关系

(29)

式中:N为声波导模态的阶数；εw,n和ζw,n分别为中间声场2中正行波和负行波的幅值；φw,n(x,kn,x)为夹层声场在x轴方向的声波导模态函数。声压速度势函数Φw,2(x,z;t)同样满足边界条件式(8)和式(9)，代入可得

(30)

(31)

其中，

由振动模态函数的正交性，由式(3)和式(4)可以得到

(32)

(33)

式中:

Λmn、Γ1,nk和Γ2,nk为声腔模态与结构振动模态之间的耦合系数；将式(30)～式(31)代入式(32)～式(33)，整理得到

通过上述计算求解，可以得到上下两弹性梁的振动模态系数α1,m和α2,m，从而求得βm、εw,n、ζw,n和ξm的值。其中φw,n(x)按照声腔边界条件来选取。当边界为刚性边界和绝对软边界时，φw,n(x)分别可以选取为

2.4 声功率

声场的声功率定义为

(34)

式中:d为梁的宽度;d=A/t;A为梁的截面积;t为梁的厚度;L为梁的长度。Δli为第i个单元长度，Nx为单元的总数，pi为第i个结构单元表面附近声场声压。

利用式(34)计算声场的声功率，假设入射声场的声功率为Π1，辐射声场的声功率为Π2，定义结构的传声损失(Sound Transmission Loss, STL)为

(35)

3 仿真计算

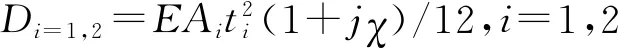
表1 夹层结构相关参数

本文计算在频率区间0～5 000 Hz内采取不同夹层处理方法时对结构传声损失曲线的影响。在不同结构参数下，结构模态和声场模态的阶数按照表2选取，保证覆盖整个计算频段和计算结果的收敛。

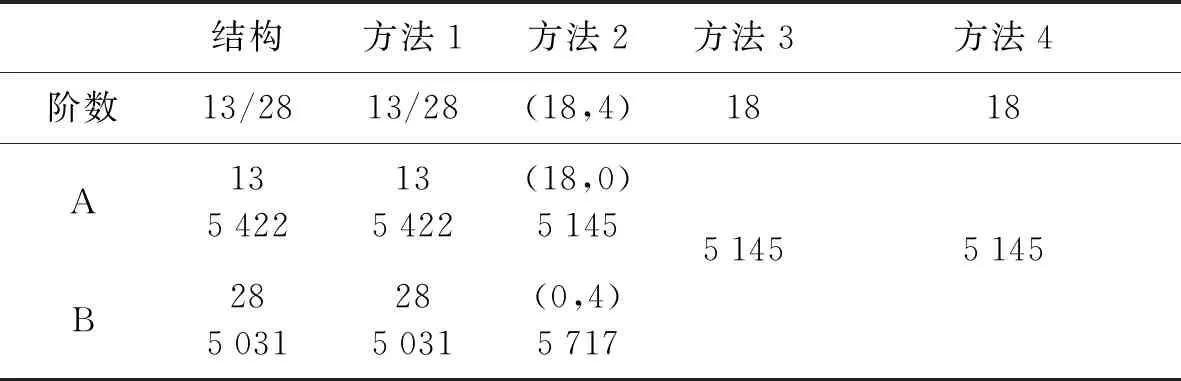
表2 结构模态和声场模态的阶数

图2为上下面板都选择A组参数时得到的结构传声损失曲线；图3为上下面板都选择B组参数时得到的结构传声损失曲线；图4为上面板选择A组参数，下面板都选择B组参数时得到的结构传声损失曲线；图5为上面板选择B组参数，下面板都选择A组参数时得到的结构传声损失曲线；图6为上、下梁为不同参数组合时得到的结构传声损失曲线。表3、表4和表5分别为不同结构参数下传声曲线中若干低谷所对应的频率值，包括结构共振频率、‘梁-空气-梁’共振频率以及驻波共振频率。

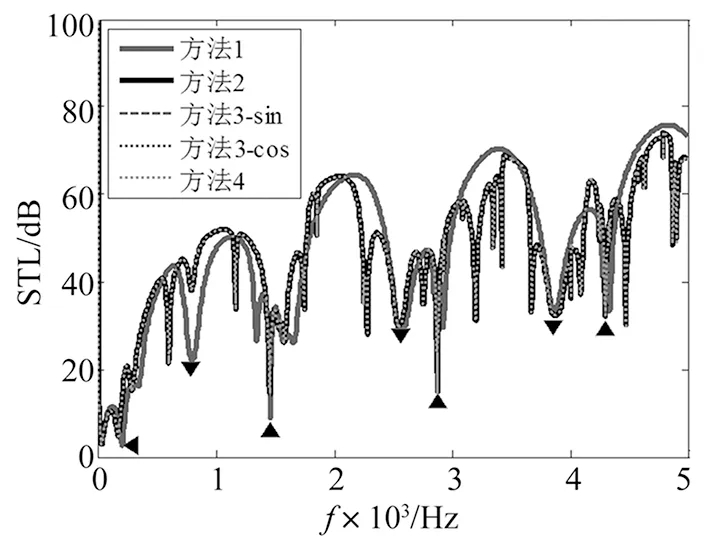
图2 上下面板均为A组参数时的传声损失曲线

声波垂直入射时，结构的共振频率fs,n，系统的“梁-空气-梁”共振频率fα和声场的声模态频率fk,l的预测计算公式分别为[5]

(36)

(37)

(38)

当k=0，则夹层的驻波共振频率为

(39)

代入对应的数值计算，图2～图5曲线中对应的“梁-空气-梁”共振频率和驻波共振频率值在表2中已列出。对比传声损失曲线和表中数值，可以解释曲线中低谷出现的原因，即由结构共振、‘梁-空气-梁’共振以及驻波共振共同作用产生。

表3 结构共振频率

表4 ‘梁-空气-梁’共振频率

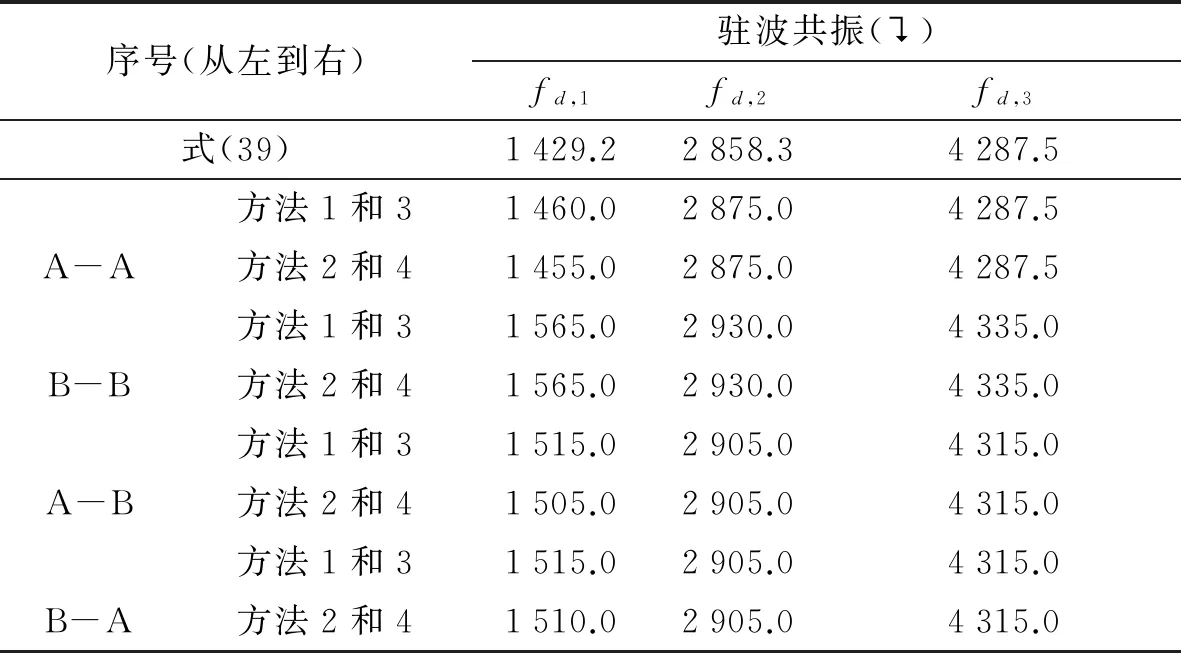
表5 驻波共振频率

从图2～图5可知，夹层声场采用声模态展开形式和声波导模态展开形式得到的传声损失曲线重合，即两种声场表示方法在反映结构的隔声性能上是等价的；然而，两种表示方法是基于不同的物理视角来考虑，声模态展开方法认为夹层声场中形成驻波声场，声场内声压由各阶声模态线性叠加而成；而声波导模态展开形式将夹层看作声波导，夹层声场声压由声波导模态线性叠加而成，利用声场与结构表面的速度连续条件求解各阶模态系数。

从图2～图5又可知，结构模态展开形式和夹层的横向声模态函数展开方法得到的结构传声损失曲线完全重合，即两种声场表示方法在反映结构的隔声性能上是等价的。同样地，两种表示方法也基于不同的物理视角，其中结构模态展开形式认为由于夹层是密封的空气腔，则空气腔内的声压分布在平行于结构平面的平面上是结构模态函数的级数形式；而夹层的横向声模态函数展开方法则认为在平行于结构平面方向形成驻波声场，且x轴方向波数与结构中弯曲波波长相等。

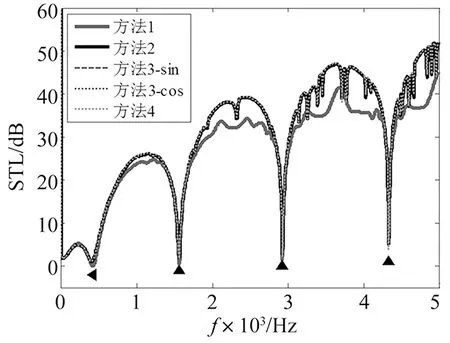
图3 上下面板均为B组参数时的传声损失曲线

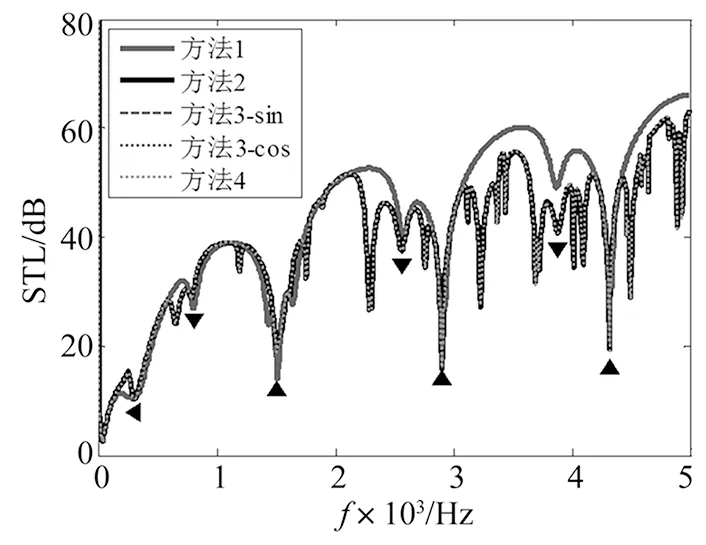
图4 上下面板分别为A组和B组参数时的传声损失曲线

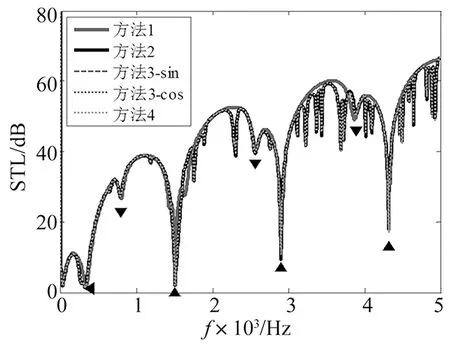
图5 上下面板分别为B组和A组参数时的传声损失曲线

对于方法3，夹层的横向声模态函数分别选取了刚性边界和绝对软边界两种情况，即边界速度为零和边界声压为零。图2～图5的计算结果表明两类边界条件得到的结构传声损失曲线安全重合。从能量的角度考虑，在刚性边界和绝对软边界两种情况下，夹层声场有相同的能量存储，而没有能量的耗散，因此得到的传声损失曲线相同。

通过上述分析，四种计算方法可以分为两类。不同的结构参数，不同的计算频段;两类计算方法得到的结构传声损失曲线有明显的差异。当上下梁的结构刚度都较大时，两类计算方法得到的传声损失曲线在整个频段都有明显的差异；而当上下梁结构中至少有一根的刚度较小时，两类计算方法得到的传声损失曲线在低频段基本吻合，而在高频段有明显的差异。

从前面的分析知道，传声损失曲线中的隔声低谷由结构共振、‘梁-空气-梁’共振以及驻波共振共同作用的结果。从图2～图5可知，结构模态展开形式和夹层的横向声模态函数展开方法可以反映结构共振、‘梁-空气-梁’共振以及z轴方向驻波共振对结构传声损失的影响，而没有反映出x轴方向驻波共振和夹层的声模态对结构隔声性能的影响；相比之下，夹层的声模态展开形式和声波导模态展开形式既反映了结构共振、‘梁-空气-梁’共振以及z轴方向驻波共振对结构传声损失的影响，也反映出x轴方向驻波共振和其余的夹层声模态对结构隔声性能的影响，因此在其对应的传声损失曲线中有更多的隔声低谷。

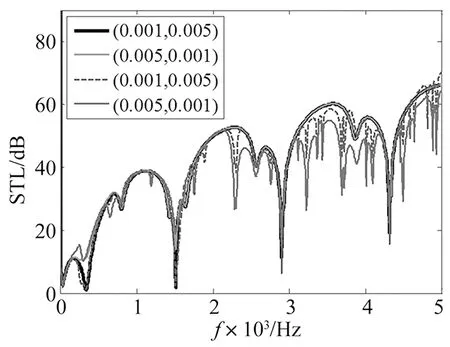
图6 上下梁为不同参数组合时的传声损失曲线

结构的厚度的变化可以看作结构刚度的变化，从表3～表5中可知：结构的刚度对系统的结构共振频率、‘梁-空气-梁’共振频率以及驻波共振频率的预测有显著的影响。从表3～表5和图3中可知：当结构刚度较小时，结构共振对系统隔声性能的影响不明显。除过结构共振、‘梁-空气-梁’共振以及驻波共振以外，系统的隔声性能还受夹层横向驻波共振和其余的声模态共振的影响，在图2～图5中，声模态展开方法和声波导模态展开方法得到的传声损失曲线中有更多的隔声低谷，其由横向驻波共振和其余的声模态共振引起。

图6反映了上下梁为不同参数时两类结构传声损失计算方法得到的传声损失曲线。从图中可以看出，上下梁厚度分别选取(0.001 m,0.005 m)和(0.005 m,0.001 m)时，结构模态展开方法和夹层的横向声模态函数展开方法得到的传声损失除过在‘梁-空气-梁’共振频率点和驻波共振频率点处大小不同之外，在其他频段完全重合；而夹层的声模态展开方法和声波导模态展开方法得到的传声损失曲线在低频段基本吻合外，特别在高频段，得到的传声曲线有明显的差异，可以看出，在高频段，当入射声场一侧结构的刚度大于辐射声场一侧的结构刚度时，结构的隔声性能大于入射声场一侧结构的刚度小于辐射声场一侧的结构刚度的情况。

其波数完全有夹层声场的几何参数决定；而声波导展开方法：

因此，声模态展开方法可以看作声波导模态展开方法的特殊情况。总之，从不同的物理视角研究夹层声场的表示方法，对于研究复杂结构或复杂边界条件下结构的声振耦合特性有一定的指导意义。

4 结 论

本文以二维双层弹性梁为模型研究了夹层结构中夹层边界对结构传声损失的影响，提出了夹层的横向声模态函数展开方法和声波导模态函数的夹层声场表示方法，并与结构模态展开形式和声腔纯模态展开形式下结构的传声损失性能曲线作对比。计算表明夹层的横向声模态函数展开方法与结构模态展开方法在计算结构传声损失上是等价的；声波导模态函数展开方法在计算结构传声损失上与声腔模态展开方法是等价的；但是，四种夹层处理方法具有不同的物理含义，声模态展开方法认为夹层声场中形成驻波声场,而声波导模态展开形式将夹层看作声波导,结构模态展开形式认为由于夹层是密封的空气腔，则空气腔内的声压分布在平行于结构平面的平面上是结构模态函数的级数形式；而夹层的横向声模态函数展开方法则认为在平行于结构平面方向形成驻波声场，波数与结构中弯曲波波长相等。计算表明：结构的传声损失曲线中的隔声低谷由结构共振、‘梁-空气-梁’共振以及驻波共振共同作用产生的结果；结构模态展开方法和夹层的横向声模态函数展开方法可以反映结构共振、‘梁-空气-梁’共振以及纵向驻波共振对结构传声损失的影响，相比之下，除此而外，夹层的声模态展开形式和声波导模态展开还反映了横向驻波共振和其余的声模态对结构隔声性能的影响，因此在其对应的传声损失曲线中有更多的隔声低谷；在高频段，当入射声场一侧结构的刚度大于辐射声场一侧的结构刚度时，结构的隔声性能大于入射声场一侧结构的刚度小于辐射声场一侧的结构刚度的情况。从不同的物理视角提出结构的隔声性能分析方法，对研究结构的隔声性能和结构的声学设计有很好的指导意义。

[1] ANTONIO J M P, TADEU A, GODINHO L. Analytical evaluation of the acoustic insulation provided by double infinite walls [J]. Journal of Sound and vibration, 2003, 263(1): 113-129.

[2] KROPP W, REBILLARD E. On the air-borne sound insulation of double wall constructions [J]. Acta Acustica united with Acustica, 1999, 98(5): 707-720.

[3] LONDON A. Transmission of reverberant sound through double walls [J].Journal of the Acoustical society of America, 1950, 22(2): 270-279.

[4] VILLOT M, GUIGOU C, GAGLIARDINI L. Predicting the acoustical radiation of finite size multi-layered structures by applying spatial windowing on infinite structures [J]. Journal of Sound and vibration, 2001, 245(3): 433-455.

[5] 卢天健，辛锋先. 轻质板壳结构设计的振动和声学基础 [M]. 北京：科学出版社, 2012.

[6] CHEN L, LI Y Y, GAO J X. Energy transmission in a mechanically-linked double-wall structure coupled to all acoustic enclosure [J]. Journal of the Acoustical Society of America, 2005, 117(5): 2742-2751.

[7] XIN F X, LU T J, CHEN C Q. Sound transmission through simply supported finite double-panel partitions with enclosed air cavity [J]. Journal of Vibration and Acoustics-Transactions of the ASME, 2010, 132: 011008.1-011008.11.

[8] DOWELL E H, GORMAN G G, SMITH D A. Acoustoelasticity： general theory, acoustic natural modes and forced response to sinusoidal excitation, including comparisons with experiment[J]. Journal of Sound and Vibration, 1977, 52(4): 519-542.

A treatment methods for a sound field of sandwich structures

NING Shaowu, SHI Zhiyu

(State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Taking a two-dimensional double-beam structure for example, the treatment methods for a sound filed of sandwich structures valleys, from different physical perspectives. The transverse acoustical modal expansion (TAME) method and acoustical waveguide modal expansion (AWME) method were presented to express the velocity potential of an air gap sound field of a sandwich structure and to compare the sound transmission losses of structures having different parameters combinations with those using the acoustical modal expansion (AME) method and structural modal expansion (SME) method. The calculation results showed that the TAME method is equivalent to the SME method and the AWME method is equivalent to the AME method in the aspects of computing sound transmission losses of structures; the sound insulation were studied are the combined action results of structural resonances, ‘beam-air-beam’ resonance and standing-wave resonances; the four computing methods can reflect the influences of structural resonances, ‘beam-air-beam’ resonance and standing-wave resonances in vertical and structural surface direction on the structures’ sound transmission losses; besides, the AME method and AWME method can also reflect the influences of standing-wave resonances in the direction parallel to structural surface and other acoustical modes on the structures’ sound transmission losses, so the corresponding sound transmission loss curve has more sound insulation valleys.

sandwich structure; structural modes; acoustic modes; acoustic wave-guide modes; resonance frequency

江苏省普通高校研究生科研创新计划资助项目(CXZZ13_0147); 机械结构力学及控制国家重点实验室(南京航空航天大学)自主研究课题资助(0515G01)；国家自然基金(11172131;11232007)；中央高校基本科研业务费专项资金资助; 江苏高校优势学科建设工程资助项目

2015-06-10 修改稿收到日期：2015-09-22

宁少武 男，博士生，1985年生

史治宇 男，教授，博士生导师，1967年生

TB535