有界窄带激励下扬声器静圈振动系统的主共振

杨志安 ， 王 帅

(1.唐山学院和唐山市结构与振动工程重点实验室，河北 唐山 063000； 2. 华北理工大学 机械工程学院，河北 唐山 063000)

有界窄带激励下扬声器静圈振动系统的主共振

杨志安1， 王 帅2

(1.唐山学院和唐山市结构与振动工程重点实验室，河北 唐山 063000； 2. 华北理工大学 机械工程学院，河北 唐山 063000)

根据拉格朗日麦克斯韦方程建立扬声器静圈振动系统的动力学模型，应用多尺度法得到在有界窄带随机激励下扬声器静圈振动系统的一次近似解及其稳态解，导出系统的ITO随机微分方程。采用矩法得到系统均方响应方程，并进行数值计算;分析扬声器静圈系统参数对主共振响应曲线和均方值的影响。主共振稳态解稳定的充分必要条件与系统一阶矩和二阶矩存在的充分必要条件是一样的；系统相轨随着随机扰动强度γ的增大，极限环变为扩散的极限环；增大音圈长度、磁场强度可以增大系统主共振的均方值；增大静圈电阻、阻尼系数可以减小系统主共振的均方值。

扬声器；静圈；拉格朗日麦克斯韦方程；多尺度；主共振；均方响应

扬声器主要工作原理是输入工作电压后通过电场与磁场相互作用，使振膜的各处产生振动[1]。扬声器诞生至今已有百年历史，随着生产的发展和科学技术的提高，扬声器也在不断的深化和更新。扬声器依然是高保真放音系统中最重要的环节，对扬声器理论方面的研究也仍然存在很多不足之处。因此，为了提高扬声器播放质量，减少失真，对扬声器系统振动进行深入研究非常重要。

文献[1]阐述了扬声器的工作原理、种类及其内部受力情况。文献[2]研究了力学非线性与磁场非线性共同引起扬声器低频谐波的失真现象。文献[3]阐述磁场非线性对扬声器的跳变现象的影响与抑制跳变的途径。文献[4]根据拉格朗日麦克斯韦方程建立扬声器静圈系统的非线性振动方程，应用多尺度法得到亚谐共振的幅频响应曲线。文献[5]根据拉格朗日麦克斯韦方程建立扬声器动圈系统的非线性振动方程，并用多尺度法得到主共振的幅频响应曲线。

在以上扬声器系统的研究中，学者们集中研究确定性激励对扬声器系统的影响。而实际上外激励存在相位、幅值的微小随机变化。本文采用在窄带随机激励作用下的扬声器非线性随机系统，利用Lagrange-Maxwell方程，对静圈扬声器建立动力学模型，运用多尺度法对系统非线性振动方程进行分析，对其在随机激励作用下的主共振进行求解计算，得到幅频响应曲线及其系统稳态解稳定的充要条件，得到系统的均方响应及系统均方响应的存在性条件，分析比较其中各元素对均方值与共振区间的影响，对扬声器的设计与优化具有重要的参考意义。

1 静圈式扬声器系统非线性动力学方程

静圈式扬声器模型如图1所示，根据拉格朗日麦克斯韦方程可以建立其非线性动力学方程:

(1)

式(1)可变为：

(2)

式(2)为扬声器静圈振动系统的非线性随机振动方程;E为窄带随机电压激励。

式中:L1,R,m,x分别为静线圈的自感系数，电阻，质量，运动位移;k、k1分别为振动腔的线性和非线性刚度;h为力学系统的阻尼系数;B为气隙磁场磁感应强度;l2为音圈的导线长度。

图1 静圈扬声器模型

2 多尺度法分析

从式(2)可知，如果系统是线性小阻尼系统，很小的激励幅值就能激起强烈的共振。研究静圈系统的主共振时阻尼项、外激励幅值激励频率加以限制，在它前面加小参数ε。故式(2)可变为：

(3)

式中:ε≪1为小参数；μ，ω分别为系统的阻尼系数和固有频率；β为系统的非线性强度，E为窄带随机电压激励，并设：

E=Hcos(Ωt+γW(t))

(4)

式中:H为随机激励强度;Ω为随机激励的中心频率;W(t)为标准的Wiener过程，本文主要研究0≤γ≪1的情形，并应用多尺度法进行研究，多尺度法已广泛应用于确定谐和激励振动问题的研究中，近几年在随机振动问题中也有一定的应用[6-9]。设式(3)的形式解为：

x(t,ε)=x0(T0,T1)+εx1(T0,T1)+…

(5)

式中:T0=t，T1=εt分别为快、慢时间尺度。本文只对首次近似解进行讨论，计算可得：

x0(T0,T1)=A(T1)exp(iω0T0)+cc

(6)

式中:cc为前面各项的共轭项。

将式(5)代入式(3)，对比ε系数，计算可得：

(7)

3 窄带激励主共振分析

所谓主共振是指外激励频率Ω接近派生系统固有频率ω0时的共振。

(8)

将A表示为极坐标的形式：

A(T1)=a(T1)eiφ(T1)

(9)

将式(9)代入式(8)并分离实、虚部可得：

(10)

式中:η=σT1-φ(T1)+γW(T1)。由式(10)解出a和η后，可得式(3)的一次近似解为：

x=2a(εt)cos[Ωt-η(εt)]+O(ε)

(11)

先考虑γ=0的情形。此时式(10)化为确定性系统：

(12)

为求稳态振动的解a=a0，η=η0，故有a′=η′=0。于是式(12)变为：

(13)

将上述两式平方相加得幅频响应方程：

(14)

(15)

当γ≠0的情形。可设式(10)的解为：

a=a0+a1，η=η0+η1

(16)

式中:a0，η0由式(13)确定，a1，η1为摄动项。将式(16)代入式(10)，并忽略关于a1，η1的高阶项可得关于点(a0，η0)的线性化方程为：

(17)

式中:W′为零均值的高斯白噪声过程，故该方程对应白噪声激励下的线性响应问题。根据Hurwitz[10]定理，该线性化方程的稳定的充分必要条件为：

(18)

根据ITO法则，式(17)可写为：

(19)

根据矩法求出式(19)的稳态解。式(19)两边取数学期望得一阶稳态矩为：

Ea1=Eη1=0

(20)

(21)

式中:

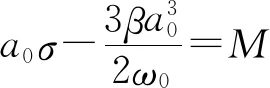
式(22)、式(23)与式(25)中M、N同上。

因为：

进而可得关于二阶稳态矩的方程：

(22)

由式(22)可得：

(23)

由式(22)可知二阶矩存在的充分必要条件为：

(24)

上述条件式(24)与式(12)稳态解的稳定性条件式(15)是一致的。式(24)同样表明在一定参数范围内式(14)可能对应三个稳态解，进而可知系式(23)对应三个均方响应值。

根据式(16)、式(20)和式(23)可得：

(25)

式(25)表明均方响应随着γ的增大将增大，随系统阻尼μ的增大而减小。

4 数值模拟

数值模拟采用的参数取值如下：

m=0.1 kg,ω0=309 Hz,B=4T,h=0.01 kg·s/m3,R=6 Ω,l2=0.004 m,k1=0.78 N/m，采用四阶龙格-库塔法计算出系统式(2)的响应。

当γ=0时，系统受简谐激励，对应不同的调谐值σ，得到扬声器静圈系统主共振幅频响应曲线。

图3为式(2)的时间历程曲线。由图3可知，有阻尼简谐激励系统振动趋于稳定。

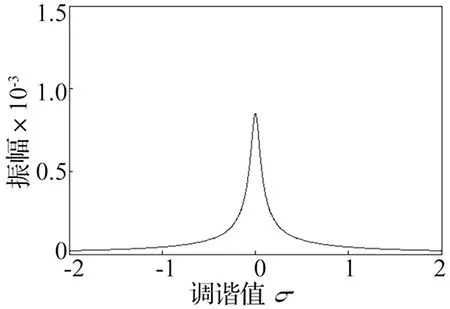
图2 幅频响应曲线

图3 时间历程图

图4为γ=0.05时，式(2)的时间历程图，由图4可知由于随机扰动的存在，系统最大振动位移呈现随机变化。

图5为图4对对应的FFT谱图，由图5可知系统振动主要频率≈5 Hz。

图4 时间历程图

图5 FFT 谱图

图6为γ=0.005，0.05，0.5时的相图，由图5可知系统相图随着随机扰动强度γ的增大，极限环宽度也逐渐增大。

图7～图10为γ=0.01时式(24)的均方响应曲线。

(a) γ=0.005的相图 (b) γ=0.05的相图 (c) γ=0.5的相图

图7 不同磁场强度时的均方响应曲线

比较图2和图7～图10可知，窄带随机激励下主共振系统均方响应曲线与γ=0时主共振系统幅频响应曲线的拓扑结构相同。

当改变静圈的磁场强度时，由图7可知,主共振均方值和共振区域随磁感应强度的增大而增大。这是因为扬声器静圈系统的电磁阻力与激励处于相同量级时，电磁阻力与磁场强度的平方成正比，激励与磁场强度成正比，增大磁场强度，可以从电磁阻力与激励两方面增大系统主共振的均方值与共振区。

当改变静圈的音圈长度时，由图8可知,主共振的均方值和共振区域随静圈音圈长度的增大而增大。这是因为扬声器静圈系统的电磁阻力与激励处于相同量级时，电磁阻力与自感系数成正比，激励与自感系数成正比，减小音圈长度，可以从电磁阻力与激励两方面减小系统主共振的均方值与共振区。

图8 不同音圈长度时的均方响应曲线

当改变静圈电阻时，由图9可知,共振的均方值和共振区域随电阻的增大而减小。这是因为扬声器静圈系统的电磁阻力与激励处于相同量级时，电磁阻力与电阻成反比，激励与电阻成反比，增大电阻，可以从电磁阻力与激励两方面减小系统主共振的均方值与共振区。

图9 不同电阻时的均方响应曲线

图10 不同阻尼时的均方响应曲线

当改变静圈阻尼系数时，由图10可知,主共振区域的均方值随阻尼系数的增大而减小。这是因为扬声器静圈系统的阻尼力与阻尼系数成正比，增大阻尼系数，可减小系统主共振的均方值与共振区。

5 结 论

应用多尺度法研究静圈式扬声器非线性主共振系统在窄带随机激励下的响应，得到主共振的幅频响应方程和系统均方响应的近似表达式，考虑了随机项对响应的影响。理论分析与数值计算表明改变扬声器静圈系统的参数，其响应的均方值也随之改变。系统相轨随着随机扰动强度γ的增大，极限环变为扩散的极限环，且宽度也逐渐增大；增大音圈长度、磁场强度可以增大系统主共振的均方值与共振区域；增大静圈电阻、阻尼系数可以减小系统主共振的均方值与共振区域。通过对比分析发现，当γ很小时，扬声器静圈系统随机过程E(t)的性态和简谐激励很接近[11]。通过计算得到静圈式扬声器主共振系统稳态解稳定的充分必要条件与系统一阶矩和二阶矩存在的充分必要条件是相同的，其内在联系需要进一步证明。

[ 1 ] 王以真. 静电扬声器的理论与实践[J]. 电声技术，2002， 2(2)：47-51. WANG Yizhen. Theory and practice of electrostatic loudspeaker [J]. Electro Acoustic Technology,2002, 2(2): 47-51.

[ 2 ] 宗丰德，张志良. 扬声器低频谐波失真的数值分析[J]. 声学技术，2003，22(2)：83-86. ZONG Fengde, ZHANG Zhiliang. Numerical analysis of total harmonic distortion of a loudspeaker in low frequency range[J]. Acoustic Technology,2003,22(2): 83-86.

[ 3 ] 陶擎天，倪皖荪，谬国庆，等. 强迫力非线性对动圈扬声器跳变现象的影响[J]. 电声技术，1989(4)：1-5. TAO Qingtian, NI Wansun, LIAO Guoqing, et al. The influence of exacted force nonlinearity about jamp phenomenon in moving-coil loudspeakers[J].Electro Acoustic Technology,1989(4): 1-5.

[ 4 ] 杨志安，张玉佳. 扬声器动圈振动系统主共振[C]// 中国力学学会《工程力学》编委会. 第21届全国结构工程学术会议论文集第Ⅲ册[C]//中国力学学会《工程力学》编委会,2012:439-443.

[ 5 ] 李健. 扬声器系统非线性振动动力学的研究[D]. 唐山： 河北联合大学，2013.

[ 6 ] 徐伟，方同，戎海武. 有界窄带激励下具有黏弹项的Duffing振子[J]. 力学学报，2002，34(5)：764-771. XU Wei, FANG Tong, RONG Haiwu. Duffing oscillator with visco-elastic term under narrow-band random excitation [J]. Journal of Mechanics,2002,34(5): 764-771.

[ 7 ] RONG Haiwu, XU Wei, FANG Tong. Principal response of duffing oscillator to combined deterministic and narrow-band random parametric excitation[J]. Journal of Sound and Vibration, 1998, 210(4): 483-515.

[ 8 ] RONG Haiwu, MENG Guang, FANG Tong. On the almost-sure asymptotic stability of second-order linear stochastic system[J]. Journal Sound and Vibration,2000,229(3): 491-503.

[ 9 ] ZHU W Q. Stochastic jump and bifurcation of a duffing oscillator under narrow-band excitation[J]. Acta Mechanica Sinica,1994, 1: 73-81.

[10] 朱位秋. 随机振动[M]. 北京：科学出版社，1992.

[11] NAYFEH A H, SERHAN S J.Response statistics of nonlinear systems to combined deterministic and random excitation[J]. International Journal of Nonlinear Mechanics, 1990, 25(5): 493-509.

Primary resonance of static coil vibration system of loudspeakers subjected to narrow-band random excitation

YANG Zhian1, WANG Shuai2

(1. Key Laboratory of Structure and Vibration Engineering, Tangshan City and Tangshan College, Tangshan 063000, China；2. College of Mechanical Engineering, North China University of Science and Technology, Tangshan 063000, China)

Dynamic model of static coil vibration system of loudspeakers was established based on Lagrange-Maxwell equation. By means of the multi-scale method, the first approximation solution and its steady state solution to the static coil vibration system of loudspeakers subjected to narrow-band random excitation were obtained. Its ITO stochastic differential equation was deduced. Using the moment method, the mean-square response equation of the system was derived and the numerical calculation was done. The influences of parameters of the static coil vibration system of loudspeakers on the primary resonance response curves and their mean-square values were analyzed. It was shown that the sufficient and necessary conditions for the stability of the primary resonance are the same as those for the first order moment and the second order moment of the response of the system; with increase in the random disturbance intensity, the limit cycle of the system becomes the limit cycle of diffusion; with increase in length of the coil and the magnetic field strength, the mean square values of the primary resonance of the system increase; the mean-square values of the primary resonance of the system decrease with increase in resistance and damping coefficient of the static coil vibration system.

loudspeaker; static coil; Lagrange-Maxwell equation; multi-scale method; primary resonance; mean square response

河北省自然科学基金项目(A200900097)

2015-09-01 修改稿收到日期：2015-11-06

杨志安 男，教授，博士，1963年生

王帅 男，硕士，1989年生

O324