基于可控冲程主被动调谐质量阻尼器的性能

曹黎媛, 李春祥

(上海大学 土木工程系，上海 200072)

基于可控冲程主被动调谐质量阻尼器的性能

曹黎媛, 李春祥

(上海大学 土木工程系，上海 200072)

提出了基于可控冲程的主被动调谐质量阻尼器(简称为CS-APTMD)。CS-APTMD是在主被动调谐质量阻尼器(APTMD)的基础上，在主体结构与小质量块之间设置一个附加粘滞阻尼装置而构成;经定义CS-APTMD的最优参数评价准则，在频域内，数值研究了在控制结构位移响应时质量比对CS-APTMD最优参数和有效性以及冲程的影响；并与APTMD的结果进行了比较。数值分析表明，CS-APTMD的控制性能显著地优于APTMD。

结构振动控制；可控冲程；主被动调谐质量阻尼器；优化；性能

主被动调谐质量阻尼器[1-2](active-passive tuned mass damper，APTMD)是一种有效的混合控制系统。这种控制系统充分利用了被动控制与主动控制各自的优点，既可以通过被动控制系统大量耗散振动能量，又可以利用主动控制系统来保证控制效果或水平。NISHIMURA等[3]对APTMD的研究发现：APTMD中ATMD的尺寸明显小于一般的ATMD；为达到某一振动抑制水平，APTMD较ATMD需要更小的控制力；而且APTMD中的TMD又能够切断APTMD中ATMD的高频振动，阻止其到达结构。此后，众多学者对APTMD展开了深入研究[4-8]。李春祥[9]进一步提出了一种新控制策略—多重主被动调谐质量阻尼器(MAPTMD)。本文在APTMD的研究基础上，提出基于可控冲程的主被动调谐质量阻尼器(CS-APTMD)装置，以期进一步提高APTMD的控制性能。

1 CS-APTMD的最优性能准则

结构-CS-APTMD系统的力学模型如图1所示。结构-CS-APTMD系统的动力方程可表示为：

(1)

(2)

(3)

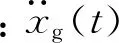
设CS-APTMD的主动控制力生成模式为：

(4)

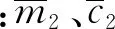
图1 基于可控冲程的主被动调谐质量阻尼器

引入变量：

ξs为主结构阻尼比；ξT为TMD阻尼比；ξt为ATMD阻尼比；ξL为附加黏滞阻尼比；μT为TMD与结构的质量比；μt为ATMD与结构的质量比；η为ATMD与TMD的质量比；αt标准化加速度反馈增益系数。

(5)

(6)

(7)

式中：

定义设置CS-APTMD结构系统、TMD冲程和ATMD冲程的动力放大系数：

(8)

(9)

(10)

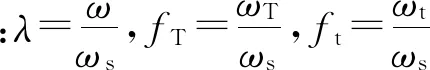
ReT(λ)=MRe(λ)-NIm(λ)

ImT(λ)=NRe(λ)+MIm(λ)

Ret(λ)=MRe(λ)-NIm(λ)

Imt(λ)=NRe(λ)+MIm(λ)

E12=-2[(1+η)ξt+ξL]ftλ

F12={[-2(ξt+ξL)ftλ](1-ηαt)-2ηξtftλ(1+αt)}λ2

E22=-2(ξLft-ξTfT)λ

F22=[-2ξLftλ(1-ηαt)+2ξTfTλ(1+αt)]λ2

为了对参数fT、ft、ξT、ξt和ξL进行优化，定义CS-APTMD的优化目标函数即最优参数评价准则为：

RHs=min.max.(DMFHs)

(11)

上述优化目标函数(11)表示：使用GA算法，针对求得的位移动力放大系数DMFHs[式(8)]最大值，在参数fT、ft、ξT、ξt和ξL的变化范围内，寻找最大DMFHs的最小值，从而获得CS-APTMD的最优参数。

2 CS-APTMD的最优性能研究

根据CS-APTMD的最优参数评价准则，使用遗传算法(GA)对CS-APTMD的性能进行数值优化，并与APTMD的结果进行比较。参数设置范围：fT=0.8～1.0，ft=0.0～1.0，ξT=0～0.999，ξt=0～0.999，ξL=0～0.999，ΔfT=0.001，Δft=0.001，ΔξT=0.001，Δξt=0.001，ΔξL=0.001，λ=0～2。GA优化得到μT=0.01和η分别取0.25、0.5、0.75、1.0时，DMFHs、fT、ft、ξT、ξt、ξL、DMFHT、DMFHt随αt的变化曲线(图2～图8)。

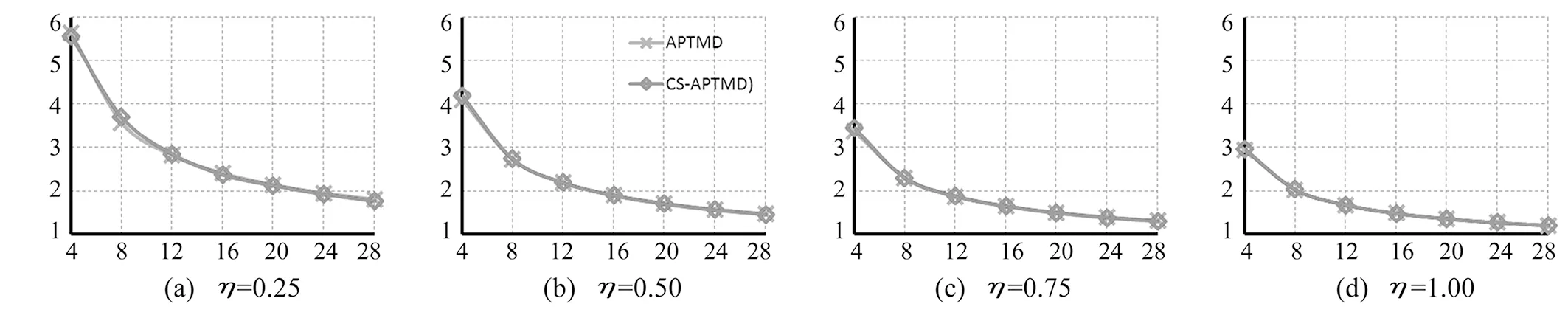
图2 APTMD和CS-APTMD的DMFHs随αt变化趋势

图3 APTMD和CS-APTMD的fT随αt变化趋势

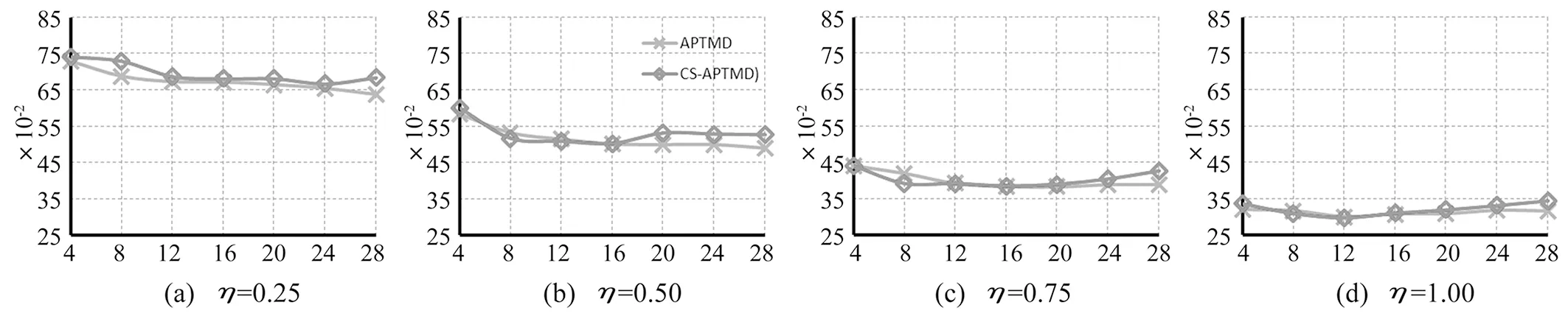
图4 APTMD和CS-APTMD的ft随αt变化趋势

由图2知，对于结构-CS-APTMD系统，结构的位移动力放大系数DMFHs随着η和驱动力αt的增大而减小，即意味着有效性越来越好。但当η>0.5且αt>12时，总体上，增大η和αt，CS-APTMD的控制有效性提高不明显。而且，重要地发现，CS-APTMD的有效性和APTMD的有效性几乎相同。由图3和图4知，随着驱动力αt和质量比η的增大，CS-APTMD的频率比fT和ft变化趋势与APTMD的频率比fT和ft变化趋势总体上相似。对于阻尼比ξT，经大量的数值分析，发现最优值ξT=0。因此，大质量块即TMD不需要安装阻尼装置。

图5 APTMD和CS-APTMD的ξt随αt变化趋势

由图5知，总体上，CS-APTMD的阻尼比ξt明显小于APTMD的阻尼比ξt。由图6知，CS-APTMD的阻尼比ξL随着αt的增大而增大。由图7知，当αt=4时，相对于APTMD，CS-APTMD的大质量块冲程DMFHT减小了50%～66%；当αt=8时，相对于APTMD，CS-APTMD的大质量块冲程DMFHT减小了22%～43%。因此，CS-APTMD的大质量块冲程明显减小，可以选择的增益范围扩大了。由图8知，当αt=4时，相对于APTMD，CS-APTMD的小质量块冲程DMFHt减小了60%～83%；当αt=8时，相对于APTMD，CS-APTMD的小质量块冲程DMFHt减小了57%～80%。因此，在冲程方面，CS-APTMD具有绝对的优势。

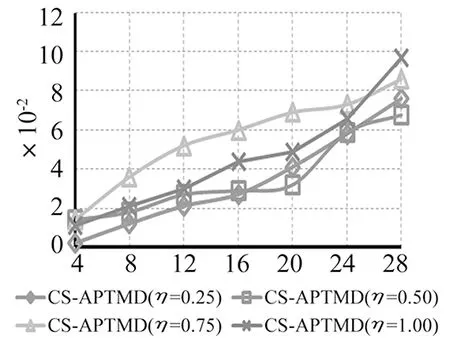
图6 CS-APTMD的ξL随αt变化趋势

图7 APTMD和CS-APTMD的DMFHT随αt变化趋势

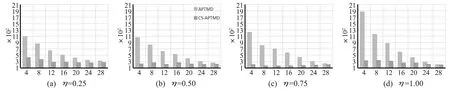
图8 APTMD和CS-APTMD的DMFHt随αt变化趋势

综合考虑CS-APTMD的控制有效性、冲程以及其参数的经济合理性三个因素，本文建议选择表1中A、B、C和D的四组数据。根据这四组参数设计的CS-APTMD，其控制性能显著地优于APTMD。

表1 μT=0.01时CS-APTMD的最优设计参数

3 结 论

本文提出了基于可控冲程的主被动调谐质量阻尼器(CS-APTMD)装置。通过理论推导及定义的CS-APTMD最优参数评价准则，使用遗传算法(GA)优化，在频域内数值研究了CS-APTMD的最优控制性能，并与APTMD进行了比较。数值分析表明，CS-APTMD的控制性能明显优于APTMD。具体地，在冲程方面，CS-APTMD具有绝对的优势；大质量块即TMD不需要安装阻尼装置。同时，论文提供了CS-APTMD的参数设计表，为工程应用时参考。

值得指出，本文使用单自由度体结构模型，研究了CS-APTMD的最优控制性能；对于多自由度结构，可以采用振型分解法，并使用本文的研究结果来设计CS-APTMD。

[ 1 ] NISHIMURA I, SAKAMOTO M, YAMADA T, et al. Acceleration feedback method applied to active-passive composite tuned mass damper[J]. Journal of Structural Control, 1994, 1(1/2):103-116.

[ 2 ] FUKUSHIMA I, SASAKI K, NISHIMURA I, et al. Development and application of active-passive composite tuned mass damper to high-rise building[C]// Proceedings of Pacific Conference on Earthquake Engineering, Australia, 1995:267-276.

[ 3 ] NISHITANI A, INOUE Y. Overview of the application of active/semi-active control to building structures in Japan[J]. Earthquake Engineering and Structural Dynamics,2001,30(11): 1565-1574.

[ 4 ] NISHIMURA I, KOBORI T, SAKAMOTO M, et al. Active passive composite tuned mass damper[C]// Proceedings of the Seminar on Seismic Isolation, Passive Energy Dissipation and Active Control, San Francisco, 1993: 737-748.

[ 5 ] NISIHIMURA I, YAMADA T, SAKAMOTO M, et al. Control performance of active-passive composite tuned mass damper[J]. Smart Materials & Structures, 1998, 7: 637-653.

[ 6 ] YAN N, WANG C M, BALENDRA T. Composite mass dampers for vibration control of wind-excited towers[J]. Journal of Sound and Vibration, 1998, 213(2): 301-316.

[ 7 ] WANG C M, YAN N, BALENDRA T. Control on dynamic structural response using active-passive composite-tuned mass dampers [J]. Journal of Vibration and Control, 1999, 5: 475-489.

[ 8 ] SHI Weixing, SHAN Jiazeng, LU Xilin. Modal identification of Shanghai world financial center both from free and ambient vibration response[J]. Engineering Structures,2012,36:14-26.

[ 9 ] LI Chunxiang. Multiple active-passive tuned mass dampers for structures under the ground acceleration[J]. Earthquake Engineering and Structural Dynamics,2003, 32(6): 949-964.

Performances of active-passive tuned mass dampers based on controlled stroke

CAO Liyuan, LI Chunxiang

(Department of Civil Engineering，Shanghai University，Shanghai 200072, China)

The controlled stroke-based active-passive tuned mass dampers (CS-APTMD) were proposed here. More specifically, an added viscous damping device was placed between the main structure and the smaller mass block of a APTMD to form a CS-APTMD. In order to study the optimal performance of a CS-APTMD, an optimization criterion was defined. Employing this defined criterion, the influences of mass ratio on optimal parameters and effectiveness, and stroke of a CS-APTMD were numerically studied in frequency domain when the displacement responses of the structure with the CS-APTMD were controlled. Furthermore, for the purpose of comparison, the optimal performances of the corresponding APTMD was also investigated. The numerical results showed that the controlling performances of a CS-APTMD are superior to those of the corresponding APTMD.

structural vibration control; controlled stroke; active-passive tuned mass dampers; optimization; performance

2015-06-23 修改稿收到日期：2015-11-08

曹黎媛 女，硕士生，1991年生

李春祥 男，教授，博士生导师，1964年生

TU311