FRFT循频滤波及齿轮微弱故障特征提取

梅检民， 贾继德， 曾锐利， 王国威， 杨万成， 周 斌

(1. 军事交通学院 军用车辆系，天津 300161； 2．天津大学 机械工程学院，天津 300072)

FRFT循频滤波及齿轮微弱故障特征提取

梅检民1，2， 贾继德1， 曾锐利1， 王国威1， 杨万成1， 周 斌1

(1. 军事交通学院 军用车辆系，天津 300161； 2．天津大学 机械工程学院，天津 300072)

提出了一种分数阶傅里叶变换(Fractional Fourier Transform, FRFT)循频滤波方法，贴近瞬变工况下信号频率曲线变化特征，循迹剥离包含故障信息的特征分量，提取齿轮早期故障微弱特征。首先，研究了线性多尺度分段方法，将频率呈曲线任意变化信号自适应分成若干个频率近线性变化的信号段；然后研究了频率拟合确定FRFT滤波参数的方法，计算各段信号的FRFT滤波参数并逐段进行FRFT滤波，实现FRFT循频滤波。采用该方法对变速器加减速过程振动信号进行滤波解调分析，试验结果表明：线性多尺度分段方法，能自适应地将任一频率呈曲线任意变化信号分段成若干个频率近线性变化的信号段，且分段数较少；频率拟合确定FRFT滤波参数方法，不受振源和多分量数量影响，能准确确定各分段信号的FRFT滤波参数；该滤波方法能从变速器瞬变工况振动信号中循频提取出包含故障信息的特征分量，有效剥离其他分量和噪声干扰，对提取后的特征分量进行解调分析，能准确提取出传统方法难以识别的齿轮早期故障微弱特征。

分数阶傅里叶变换；循频滤波；微弱故障；特征提取

变速器壳体振动信号中包含多个信号分量和噪声干扰，故障信息仅隐含在对故障诊断有意义的特征分量中，当齿轮发生故障时特征分量是啮合频率调制信号，由于早期故障特征微弱，容易被其他分量和噪声淹没，难以提取[1-4]。在加速、减速和加减速等瞬变工况下，更容易暴露微弱特征，而此时的振动信号频率呈曲线变化，其他干扰也更强，需要有效的方法将包含故障信息的特征分量从其他分量和噪声中剥离出来，才能更有希望提取到暴露出的早期故障微弱特征。

由于瞬变工况下信号频率呈曲线变化，时域或频域滤波方法不能处理此类非平稳信号，自适应滤波器需要输入参考信号进行滤波，基于稀疏信号分解的自适应时变滤波器能有效滤波，但根据振动信号估计中心频率时计算量过大，需要选择合适的滤波器并设计其参数[5-6]。基于分数阶傅里叶变换(Fractional Fourier Transform, FRFT)的单阶自适应滤波，计算速度快，不需要选择和设置复杂滤波器，对多分量线性调频(Linear Frequency Modulation，LFM)信号有很好的滤波效果[7-8]；对频率呈曲线变化的信号，需要多阶FRFT自适应滤波，即在不同的分数阶域对频率呈曲线信号进行多次单阶FRFT滤波[9]，但需要准确确定多个分数阶域滤波参数。文献[10]通过对振动信号进行多尺度稀疏分解，实现了无转速计条件下的多阶FRFT滤波，确定滤波参数时必须先对振动信号进行稀疏分解，效率不高，精度受振源和多分量数量影响；文献[11]根据频率曲线曲率分段实现多阶FRFT滤波，对不同的频率呈曲线变化信号需要重新设定曲率阈值，自适应性不高。文献[12]将线调频小波路径追踪算法与FRFT相结合进行升降速齿轮故障诊断，取得了一定的效果，但该方法对每组信号都需要通过人工观察截取频率近线性变化的信号段进行分析，舍弃频率非线性变化信号段，分析信号不完整，自适应性差；该方法没有理论上计算FRFT滤波的重要参数-滤波中心，当滤波目标能量较弱、其他干扰较强时，容易因滤波中心不准确，影响诊断结果。因此，研究有效方法贴近频率曲线变化特征，循频剥离特征分量，隔离其他干扰，对齿轮早期故障微弱特征提取具有重要意义。

针对瞬变工况下齿轮早期故障特征分量难剥离、特征难提取的问题，本文提出了一种FRFT循频滤波方法：先研究线性多尺度划分方法，将频率呈曲线任意变化信号自适应分段成不同尺度下频率近线性变化的信号段，且分段数较少；然后，根据频率曲线拟合快速、准确计算FRFT滤波参数，并对各段信号依次进行FRFT单阶滤波，再顺序连接滤波后信号，从而循频提取出频率呈曲线变化的特征分量；对提取出的特征分量进行细致分析，能准确提取出齿轮早期剥落故障微弱特征。

1 FRFT及FRFT自适应滤波原理

1.1 FRFT原理[13]

信号x(t)的FRFT定义式为

(1)

式中:FRFT的变换核Kp(t,u)为

(2)

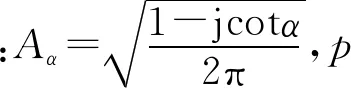
(3)

1.2 FRFT单阶滤波原理

FRFT可以解释为信号在时频平面内绕原点旋转一定角度后所构成的分数阶域上的表示，设两分量LFM信号的时频分布见图1，其中一个LFM分量的时频分布与时间轴的夹角为β，只要FRFT旋转角度α与β正交，则该LFM分量在分数阶傅里叶域上就应该聚集在u0一点上，以分数阶域聚集点u0为中心做窄带滤波，再进行-α角度旋转，就实现了LFM分量的单阶FRFT滤波，此时的α为FRFT变换最佳角度，p0=2α/π为最佳阶次。

可见，采用单阶FRFT滤波提取LFM分量的关键在于准确确定最佳阶次p0和分数阶域聚集位置u0两个参数。目前，常用的FRFT滤波参数(p0,u0)确定方法都是基于搜索思想的，即通过对图2所示的振动信号FRFT幅值谱进行峰值搜索确定FRFT滤波参数[14]。

图1 多分量LFM信号单阶FRFT滤波

图2 LFM信号FRFT幅值谱

1.3 多阶FRFT滤波及存在的问题

单阶FRFT滤波对图1中的多分量LFM信号具有很好的滤波效果，但图3中两个分量频率都呈曲线变化，只旋转一个角度的单阶FRFT自适应滤波无能为力。

图3 多阶FRFT滤波分离频率呈曲线变化的多分量信号Fig.3 Multi-component signal with curving frequency separeated by FRFT filter

文献[9]指出的多阶FRFT自适应滤波，通过依次旋转多个角度α1,α2,…,α4，在多个分数阶域u1,u2,…,u4上以u01,u02,…,u04为中心进行滤波，理论上可以分离图3所示信号，但确定合适的α1,α2,…,α4和u01,u02,…,u04比较困难。原因在于：如图4(a)所示的频率呈曲线变化的信号，会在多个分数阶域呈现聚集性，从而在FRFT幅值谱中形成多个峰值，如图4(b)所示，常用的峰值搜索方法很难确定哪个峰值是哪段信号聚集形成的，因此难以根据峰值确定各段信号的FRFT滤波阶次；当信号中存在多个频率呈曲线变化分量时，如图4(c)所示，FRFT幅值谱中峰值会更加复杂，如图4(d)所示。

图4 频率呈曲线变化信号及其FRFT幅值谱

可见，当信号中有单个或多个频率呈曲线变化分量时，信号的FRFT幅值谱中峰值非常复杂，根据峰值搜索将很难确定频率呈曲线变化信号的多个FRFT滤波参数，因此难以实现有效的多阶FRFT滤波。

从上述分析可以看出，与传统滤波相比，FRFT滤波具有许多令人青睐的优点，理论上对频率呈曲线变化分量的滤波提取具有独特的优势，但需要解决以下问题：

(1)需要有效的方法能自适应地将频率呈曲线变化的信号分成若干频率近线性变化的信号段，而且分段数尽量少；

(2)要准确确定各段信号的FRFT滤波参数(p0,u0)，只有p0准确，才能保证目标分量在该阶次的分数阶域上具有最好的聚集性，只有u0准确，才能准确滤波分离目标分量，隔离其他干扰。

2 FRFT循频滤波

为了实现瞬变工况下频率呈曲线变化信号提取，本文提出了一种FRFT循频滤波方法，主要包括两项内容：线性多尺度分段和频率拟合确定FRFT滤波参数，下面分别介绍两者的原理。

2.1 线性多尺度分段

(1)多尺度区间划分

设为I为多尺度区间，I=[kN2-j-(k+1)N2-j]，式中：j为分析尺度系数，j=0,1,…,log2N-n；N为信号采样点数，要求N为2的整数次方，n为尺度调整参数，为了使尺度不能过小，应该适当调整参数n，k=1,…,2j，表示某个尺度系数下区间序号，多尺度区间划分示意图见图5。

图5 多尺度区间划分示意图

(2)频率拟合确定投影系数

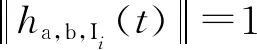
βIi≤XIi(t),ha,b,Ii(t)>

(4)

式中：βIi反应了振动信号XIi(t)与基函数ha,b,Ii(t)的相似程度。XIi(t)越近似线性调频信号，βIi值越大，反之越小。按照式(4)计算全部多尺度区间内的投影系数βI。

(3)逐尺度搜索确定线性多尺度分段路径

为了找到与信号频率曲线变化最为贴近的多尺度分段路径，需要从全部的投影系数βI内搜索出一条多尺度路径，使得该路径下的投影系数之和为最大，即：

(5)

Π覆盖整个信号时间范围且不重叠。

本文提出一种逐尺度搜索方法，实现上述路径搜索。具体原理如下：多尺度区间投影系数矩阵βI如图6所示，构建路径搜索标识集合CI，将CI最底层初始化为2，如图7所示。从βI最底层尺度开始，令βL=βI,j,k+βI,j,k+1，βH=βI,j-1,(k+1)/2，βI,j,k表示j尺度下的第k个区间的投影系数；如果βH<βL，则βI,j-1,(k+1)/2=βL；如果βH>βL，令CI,j-1,(k+1)/2=2，并令βI,j-1,(k+1)/2对应的时间范围内所有下层尺度的CI,j,k=1，CI,j,k表示j尺度下的第k个区间的搜索标识，如图8所示；根据此方法按照尺度由小到大进行搜索，搜索中j=[log2N-n,:-1:1]，k=[1:2:2j-1]，表达式d=[d1:Δd:d2]表示变量d从d1按照间隔Δd变化到d2，最后所有CI,j,k=2的多尺度区间组合就是与信号最贴近的多尺度路径；按照该多尺度路径对振动信号进行分段，即完成了频率呈曲线变化信号的线性多尺度分段。

图6 多尺度区间投影系数矩阵βI

图7 搜索标示集合CI

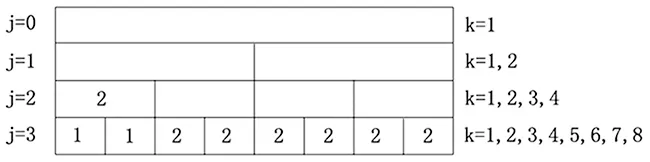
图8 搜索标示集合CI

采用逐尺度搜索方法，对某一频率呈曲线变化信号进行线性多尺度分段，结果如图9所示，该分段方法能很好贴近频率曲线变化特征进行多尺度分段，频率变化复杂时采用小尺度区间分段，频率变化缓慢时采用大尺度区间分段，既使各分段内的信号频率近似线性变化，又使分段数量较少，而且对于任一频率呈曲线变化信号，不需要重新调整参数，都能自适应地完成多尺度分段，具有很好的自适应性，完全满足多阶FRFT滤波要求。

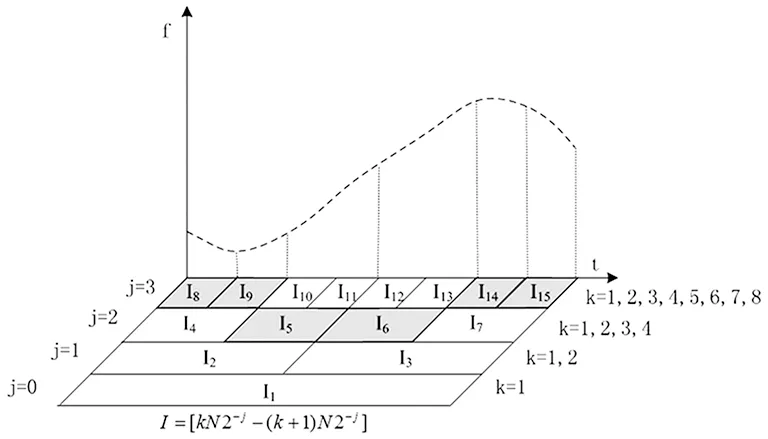
图9 逐尺度搜索线性多尺度分段路径

2.2 频率拟合确定FRFT滤波参数

(1)FRFT滤波阶次计算

从图1可以看出，最佳角度α、FRFT最佳阶次p与调频率μ0有如下关系：

(6)

结合式(6)，本文采用一种根据频率曲线计算FRFT阶次的方法：按照线性多尺度分段结果，根据各个分段内确定投影系数时的拟合频率函数fIi=a+2bt，计算各分段的FRFT滤波阶次pIi=1+(2/π)arctan(2b)。

(2)FRFT滤波中心计算

分数阶域滤波中心为信号在分数阶域上的聚集位置u0，通常需要人为观察信号在FRFT幅值谱中的能量强弱情况来确定，缺乏理论参考，加上噪声和其他分量的影响，容易错判滤波中心，导致滤波结果不正确或不准确。

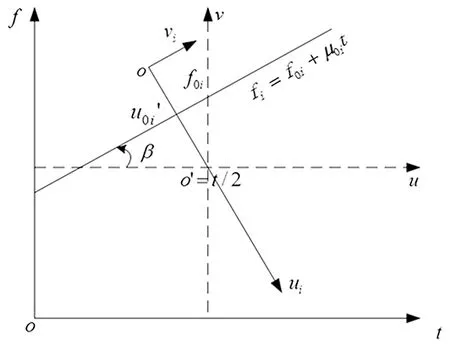
图10 分数阶域聚集位置计算

(7)

(8)

式中:S为离散尺度归一化因子。

理论计算的分数阶域聚集位置，能准确定位FRFT滤波中心，无论分量在FRFT幅值谱中能量强弱，都能根据该中心实现准确的带通滤波，是实现多分量频率呈曲线变化信号多阶FRFT滤波的关键。

由于转速信号不受任何振源和噪声干扰，采用频率拟合确定FRFT滤波参数，精度高、速度快、鲁棒性好。根据该方法确定线性多尺度分段后的各个振动信号段滤波参数并进行FRFT滤波，再顺序连接滤波结果，就实现了频率呈曲线变化信号的FRFT循频滤波。

3 齿轮早期故障微弱特征提取

3.1 实验装置

实验对象为BJ2020S变速器，有四个前进挡和一个倒档，其传动示意图如图11所示。试验装置构成如图12所示。电动机模拟发动机驱动变速器，发电机模拟负载。采用电火花在输出轴二档齿轮上加工坑点模拟早期剥落故障，以输入轴为参考轴，该齿轮故障特征阶次为0.43。变速器置二档，同步采集加减速瞬变工况的转速信号和振动信号，采样频率40 kHz，采样时间3.287 6 s。

图11 BJ2020S变速器传动示意图

图12 实验装置

3.2 故障特征提取

齿轮发生故障时，特征分量是啮合频率调制信号。变速器转频及1档～4档的啮合频率fh(h=0,1,2,3,4)如图13所示，各频率呈曲线变化，传统的时域或频域滤波都不能提取某个档位的啮合频率分量；振动信号的GABOR时频图如图14所示，时频图中峰值突出的是二档啮合频率分量，同时还包含了许多其他分量和噪声。

图13 转频及各档位啮合频率曲线

图14 振动信号时频图

采用本方法对二档加减速过程信号进行分析，二档啮合频率分量的线性多尺度分段结果如图15所示，该方法根据频率曲线变化特征划分多尺度区间，在频率变化复杂部分采用小尺度区间，在频率变化简单部分采用大尺度区间，各分段内频率都近似线性变化，满足单阶FRFT滤波要求；按照线性多尺度分段结果，采用频率拟合确定各段信号FRFT滤波参数，并进行FRFT滤波，循频提取出二档啮合频率分量，其Gabor时频图如图16所示；提取出的二档啮合频率分量很好地保持了信号的频率特征和幅值特征，证明本方法准确、有效地提取出了变速器瞬变工况下的特征分量。

图15 线性多尺度分段

图16 提取分量时频图

对原始振动信号进行阶次包络分析，结果如图17所示，在故障特征阶次0.43处，没有出现明显峰值，无法判断二档输出轴齿轮存在早期剥落故障，说明早期剥落故障微弱特征被其他分量和噪声淹没，难以提取；对本方法提取出的二档啮合频率分量进行阶次包络解调分析，结果如图18所示，在0.428 6处有突出峰值，与理论故障特征阶次0.43一致，有效诊断出二档输出轴齿轮的早期剥落故障，说明本方法有效剥离了其他分量和噪声干扰，对提取后的分量进行细致分析，更能有效提取出变速器齿轮早期故障微弱特征。

图17 原始信号阶次包络谱

图18 提取分量阶次包络谱

4 结 论

(1)线性多尺度分段方法，能自适应地将任一频率呈曲线任意变化信号分段成若干个频率近线性变化信号段，且分段数较少；

(2)频率拟合确定FRFT滤波参数方法，不受振源和多分量数量影响，能快速、准确确定各分段信号的FRFT滤波参数；采用该滤波参数对线性多尺度分段后的各个振动信号段进行FRFT滤波，实现了频率呈曲线变化信号的FRFT循频滤波；

(3)该滤波方法能从变速器瞬变工况下频率呈曲线变化振动信号中循频提取出包含故障信息的特征分量，有效剥离其他分量和噪声干扰；对特征分量进行阶次解调分析，能准确提取出难以识别的齿轮早期故障微弱特征。

[ 1 ] VISHWASH B, SRINIVASAPAI P, SRIRAM N S, et al. Multiscale slope feature extraction for gear and bearing fault diagnosis using wavelet transform[J]. Procedia Materials Science ,2014,5: 1650-1659.

[ 2 ] XU Youcai, LI Xinshi, TAO Ran, et al.. The application of local mean decomposition and variable predictive model-based class discriminate in gear fault diagnosis[J]. Advanced Materials Research, 2014, 1014: 510-515.

[ 3 ] CUI Lingli, MO Daiyi, WU Na. Application of sparse signal decomposition using dual-BP in gear-box weak fault diagnosis[J]. Chinese Journal of Science Instrument,2014, 35: 2633-2640.

[ 4 ] TIAN H, KANG X Y, LI Y J. Fault diagnosis of gear wearing based on order cepstrumanalysis[J]. Applied Mechanics and Materials,2014, 543: 922-925.

[ 5 ] 彭富强，于德介，罗洁思，等. 基于稀疏信号分解的自适应时变滤波器及其在齿轮故障诊断中的应用[J]. 机械工程学报，2010,46(24):46-53. PENG Fuqiang, YU Dejie, LUO Jiesi, et al. MSCSSD-based adaptive time-varying filter and its application to gearbox fault diagnosis [J]. Journal of Mechanical Engineering, 2010,46(24):46-53.

[ 6 ] 彭富强. 多尺度线调频基稀疏信号分解及其在齿轮箱故障诊断中的应用[D]. 长沙: 湖南大学，2010.

[ 7 ] 陈小龙，关键, 刘宁波，等. 基于FRFT的LFM信号自适应滤波算法及分析[J]. 现代雷达，2010,32(12):48-53. CHEN Xiaolong, GUAN Jian, LIU Ningbo, et al.Adaptive filtering algorithm for LFM signal and performance analysis based on FRFT [J].Modern Radar, 2010,32(12):48-53.

[ 8 ] 齐林，陶然. 基于分数阶傅里叶变换的线性调频信号的自适应时频滤波[J]. 兵工学报，2003,24(4):499-502. QIN Lin, TAO Ran. An adaptive time-frequency filtering method based on fractional fourier transform for linear frequency modulation signals [J]. Acta Armamentarii, 2003, 24(4): 499-502.

[ 9 ] 陶然，邓兵，王越. 分数阶傅里叶变化及其应用[M]. 北京：清华大学出版社, 2009.

[10] 梅检民，肖云魁，沈虹，等. 多阶FRFT自适应滤波及齿轮微弱故障特征提取[J]. 振动工程学报,2013,26(5):771-778. MEI Jianmin, XIAO Yunkui, SHEN Hong,et al. Multi-order FRFT adaptive filter and its application to extract weak fault feature based on sparse signal decomposition[J]. Journal of Vibration Engineering, 2013,26(5):771-778.

[11] 李枫，梅检民，肖云魁，等. 基于转速自适应多阶FRFT滤波提取瞬变工况齿轮微弱故障特征[J]. 振动与冲击, 2013,32(21):158-163. LI Feng, MEI Jianmin, XIAO Yunkui, et al. Extraction of gearbox fault features under transient-conditions based on self-adaptive segmentation and multilevel fractional fourier transformation filtering [J].Journal of Vibration and Shock, 2013,32(21):158-163.

[12] 罗洁思，于德介，陈向民. 线调频小波路径追踪算法和FRFT相结合的升降速齿轮故障诊断方法[J]. 机械工程学报，2012, 48(7):56-61. LUO Jiesi, YU Dejie, CHEN Xiangmin, et al. Gear Fault Diagnosis under the Speed-up and Speed-down Process Based on the Chirplet Path Pursuit Algorithm and FRFT [J],Journal of Mechanical Engineering, 2012, 48(7):56-61.

[13] 刘峰，徐会法. 分数阶Fourier变换中量纲归一化因子的选取[J].系统工程与电子技术，2011,33(2):237-240. LIU Feng, XU Huifa. Selection of dimensional normalization parameters in fractional Fourier transform [J]. Systems Engineering and Electronics, 2011, 33(2): 237-240.

[14] 臧顺全，王竹霞. 基于分数傅里叶变换的信号检测方法[J].科学技术与工程，2010，10(3)：651-655. ZANG Shunquan, WANG Zhuxia. Signal detection method based on fractional fourier transform [J]. Science Technology and Engineering, 2010, 10(3): 651-655.

[15] 赵兴浩. 分数阶傅里叶变换数值计算中的量纲归一化[J].北京理工大学学报，2005，25(4)：361-364. ZHAO Xinghao. Dimensional normalization in the digital computation of the fractional fourier transform[J]. Journal of Beijing Institute of Technology, 2005, 25(4): 361-364.

FRFT Filtering based on frequency tracking and extraction of gear’s weak fault features

MEI Jianmin1,2, JIA Jide1, ZENG Ruili1, WANG Guowei1, YANG Wancheng1, ZHOU Bin1

(1. Department of Military Vehicle, Military Transportation University, Tianjin 300161, China；2.School of Mechanical Engineering, Tianjin University, Tianjin 300072, China)

To extract weak fault features of gears, a fractional fourier transformation (FRFT) filtering method based on frequency tracking (FT) was proposed to peel the feature components containing fault information by tracking frequency and to approach varying features of a signal’s frequency curve under the transient condition. Firstly, the linear multi-scale segmentation method was studied to divide a signal frequency curve into some segments with frequency varying linearly. Then, the method to determine a FRFT filtering parameters with frequency fitting was studied to calculate FRFT filtering parameters of each signal segment, and each signal segment was filtered with FRFT filtering using these parameters. A gearbox’s acceleration and deceleration vibration signals were filtered with FFFT and the filtered signals were demodulated. The results show that the linear multi-scale segmentation method is able to adoptively divide any signal frequency curve into several segments with frequency varying linearly; the FRFT filtering parameters determined with frequency fitting of each signal segment have no influences of vibration source and number of multi-component; the feature components containing fault information in gearbox’s transient signals can be extracted with FRFT, the other components and noise are peeled at the same time; the weak features of the early fault of gear can be extracted through the demodulation analysis of the extracted feature components, they are difficult to be identified with the traditional method.

FRFT; frequency tracking filtering; weak fault; feature extraction

总装备部预研资助项目

2015-06-29 修改稿收到日期：2015-12-14

梅检民 男，博士后，讲师，1983年生

TH165+.3