有限元法在透平叶片振动研究中的应用*

2017-01-09王南飞南国防蒋东翔

振动、测试与诊断 2016年6期

关键词：振型B型固有频率

王南飞，南国防，蒋东翔

(1.清华大学热能工程系北京，100084)(2.上海理工大学能源与动力工程学院上海，200093)

有限元法在透平叶片振动研究中的应用*

王南飞1，南国防2，蒋东翔1

(1.清华大学热能工程系北京，100084)(2.上海理工大学能源与动力工程学院上海，200093)

以透平叶片振动分析理论为基础,对实验室的等截面直叶片分别通过理论法和有限元法求解其前7阶的切向弯曲自振频率并加以比较。利用有限元法对叶片及顶部围带相互连接的叶片组在不同转速下进行模态分析,得到叶片及叶片组动力刚化效应振动模态数值分析结果，并对结果进行了分析比较。对于顶部围带不连接的叶片组，利用有限元法通过构造弹簧模型来处理顶部围带的接触问题，所得结果真实反映了汽轮机运行过程中围带的碰撞和叶片的振动情况。

透平叶片; 模态分析; 有限元; 动力刚化; 弹簧模型; 接触

引言

叶片疲劳断裂是透平机械在运行过程中的一种常见事故。其原因往往是由于叶片的共振应力过大[1]。研究叶片振动的方法很多[2-8]，而通过有限元进行模态分析研究叶片及叶片组的频率和振型是其中一种行之有效的方法[9-10]。

以往在研究透平机械叶片的振动模态时，关注较多的是叶片的形状、结构及叶根阻尼[1]等因素，而工作环境对叶片固有频率及振型的影响关注比较少。实际情况中，离心力场、气动力场、温度场及热力场[11]等因素都会使叶片材料的机械性能发生变化或在叶片内部产生预应力，导致应力刚化现象，进而影响叶片的固有频率和振型[12]。孙强等[13]以某型航空发动机压气机第6级的叶片为例，研究了温度对叶片振动频率的影响。文献[14]对汽轮机叶片振动进行了研究，就静摩擦参数和动摩擦参数对叶片振动的影响进行了分析。

1 等截面直叶片模型的建立和求解

1.1 理论求解叶片切向弯曲自振频率

由文献[15]可以得到等截面直叶片切向弯曲的自振频率求解公式

(1)

其中:E为材料的弹性模量；I为叶片截面惯性矩；ρ为叶片的材料密度；F为叶片的横截面积。

根据A型振动(叶根固定、叶顶自由的振动)和B型振动(叶根固定、叶顶不动的振动)所满足的约束条件，可以得到含kl的频率方程式。A型振动频率方程式为cos(kl)ch(kl)=-1，其中l为叶高；B型振动频率方程式为tan(kl)=th(kl)。利用Matlab编程求解频率方程式，可以得到kl的值。因叶片材料已知，其密度ρ=7.75×103kg/m3，泊松比μ=0.3，弹性模量E=2.167×1011N/m2。量取实验室叶片的真实几何参数，按照1∶1在Solidworks建立叶片模型，利用Solidworks的面域属性得到叶片横截面的面积和叶片截面惯性矩，带入式(1)可得到前7阶A型振动和B型振动切向弯曲的自振频率，其求解结果如表1所示。

1.2 有限元法求解叶片切向弯曲自振频率

有限元法是将实体模型离散化近似求解连续场问题的数值方法。对于非旋转状态下的任何系统，其运动方程[16]为

Mu″+Cu′+Ku=F

(2)

其中：M为结构的质量矩阵；C为结构的阻尼矩阵；K为结构的刚度矩阵；F为外力矢量；u″为加速度矢量；u′为速度矢量；u为位移矢量。

在本研究分析过程中，可将叶片看成是一端固定在叶轮上的无阻尼自由振动的物体，因此式(2)变为

Mu″+Cu′+Ku=0

(3)

式(3)解的形式为

(4)

其中：X为模态形状；ω为固有频率。

将式(4)带入式(3)得

(5)

令λ=ω2，则式(5)存在非零解的条件为

(6)

式(5)称为广义特征方程，是λ的n次代数方程，可得

(7)

通过求解特征值式(7)，可以求得模态形状X和固有频率ωi。

研究旋转状态下的叶片动力学特性需要考虑旋转离心力的作用，由于旋转离心力的作用，叶片在旋转时会产生“动力刚化”效应[17],该效应由叶片刚体运动和弹性变形的耦合引起并导致叶片固有频率的变化。同时，叶片受旋转惯性力的影响，还需计入几何刚度矩阵，即在非旋转状态下分析方程的基础上，对刚度矩阵一项进行修改，得到[18]

(8)

其中：K0为叶片的常规有限元刚度矩阵；Kd为刚体运动与弹性变形的耦合作用产生的动力刚度矩阵；Kg为离心惯性力产生的几何刚度矩阵。

当综合考虑旋转叶片几何刚度矩阵和动力刚度矩阵时，叶片各阶固有频率随转速仍会有所增加，说明了旋转叶片存在动力刚化。只有综合考虑叶片的刚体转动和弹性变形的耦合和轴向惯性力所引起的弯曲刚度的变化，才能够得到较为精确的旋转叶片的动力特性分析结果[18]。

通过改变旋转转速可以改变Kg的大小，从而得到不同转速下的固有频率与振型图。因此旋转状态下叶片动力学特性分析方程[18]为

(9)

对于本研究中的透平等截面直叶片，首先利用Solidworks建立三维实体模型，所建立的模型如图1所示。由于有限元软件ANSYS的分析模块与Solidworks是无缝集成的，将三维实体模型保存为x_t格式，以便ANSYS读取。针对叶片自身形状和材料的特点，采用solid185单元，运用ANSYS的MESHING功能，对叶片进行网格划分。A型振动和B型振动约束和划分网格后的模型如图2所示。其中图2(a)中的叶片单元数为497 921，图2(b)中有542 888个单元。按照有限元分析的一般步骤，直接在ANSYS中进行边界设置、求解控制等操作，边界设置时对叶根进行全约束，把叶根x,y,z方向的自由度都约束为0。

图1 真实叶片和Solidworks建立的叶片模型Fig.1 Real blade and 3D model by the Solidworks

图2 叶片的有限元模型Fig.2 FEM model of turbine blade

图3 前3阶切向弯曲振动振型Fig.3 The first three-order tangential bending vibration modes

利用ANSYS分析得到A型和B型切向弯曲振动的前7阶自振频率，如表1所示。同时从图3振型中(只列举前3阶切向弯曲振动)可清晰地看出，无论对于A型振动(左侧)还是B型振动(右侧)，振动过程中出现的节点(振型中保持不动的点)和理论分析的结果很吻合。

表1 切向弯曲振动前7阶自振频率

由表1可得，通过理论计算和有限元求解得到的A型振动和B型振动的前4阶自振频率值非常接近。之所以只看前4阶的自振频率，是因为当频率越大时，振幅越小，后面的高自振频率即使出现，也不危险。导致误差的原因有ANSYS分析时所选的单元类型的合适程度、划分网格的精细程度及数字信号分析误差等。

1.3 考虑动力刚化时叶片模态计算结果

在实际的运行状态下，由于离心力载荷的作用，叶片产生拉伸变形，模态有可能与静止状态产生很大差别，所以必须予以考虑。影响旋转件频率变化的一种原因是由于离心力对叶片运动产生的预应力的影响，造成了叶片刚度的增加，从而使模态频率升高。

对于做A型振动和B型振动的等截面直叶片，其约束方式与做固有频率分析时的约束方式相同，并根据叶轮尺寸确定叶片旋转的旋转轴。在不同转速下利用ANSYS做静态分析，求出对应的离心力作为预应力，然后再进行模态分析。分别求解叶片在转速为0，3，6，9 kr/min下考虑刚化效应的前7阶固有频率。约束并划分网格然后进行求解，A型振动和B型振动求解后前7阶的频率结果如表2所示，其第1,2阶频率随转速关系如图4所示。

表2 动力刚化对叶片固有频率的影响

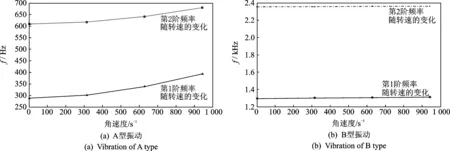
图4 第1，2阶频率随转速的变化Fig.4 Relationship between the natural frequency and rotate speed

由表2可以看出，无论是A型振动还是B型振动，刚化效应对叶片振动频率的影响是随叶片转速增加而增大。表2中对应A型振动，在透平机械转速为6kr/min时，叶片刚化效应对其固有频率已有较大影响，第1阶切向弯曲振动频率从288.45Hz变为301.74Hz，相应的轴向弯曲振动频率从608.39Hz变为616.31Hz。从图4(a)中可以看出，第1，2阶频率随转动角速度变化的趋势也表明，旋转叶片存在动力刚化，对频率的影响随转动角速度增大而增大，同时第1阶随转速变化较快，第2阶变化较慢，说明惯性力对切向弯曲刚度的影响大于对轴向弯曲刚度的影响[19]。

由表2中对应B型振动(第1，2行)和图4(b)可看出，随着转速的增大，频率也有略微的增加，但是并没有A型振动那么明显。这是因为叶片的动频率与其转速的关系[15]有关

(10)

其中：fd为动频率；f为静频率；B为动频系数；ns为转子每秒转速。

2 考虑动力刚化叶片组模态计算结果

因为在实际运行过程中，除叶片本身在组内振动之外，整个叶片组也将产生振动。下面分析3个等截面直叶片构成的叶片组在不同转速下的频率和振型。其中叶片顶部相邻的围带之间采用ANSYS中的bonded约束方式，利用solid185和solid285两种单元类型划分网格，得到1 129 859个单元，求解静频率时对叶片根部的所有自由度都约束为0。求解动频时根据几何尺寸确定旋转轴，将叶片根部的所有自由度也都约束为0，将离心力作为预应力进行模态分析，其前7阶的频率结果如表3所示，其第1，2阶频率随转速的关系如图5所示，对应的前3阶的振型图如图6所示。图6(a)的左侧代表转速为0时前3阶的振型，图6(b)代表转速为9kr/min时前3阶的振型。

从表2和表3对应可以看出，第1阶固有频率从单叶片的288.45Hz变为323.00 Hz，第2阶固有频率从608.39Hz降为529.52Hz。这是由于透平叶片间的振动相互影响和耦合，叶片安装于叶轮之上，而叶轮并非完全刚性，计算时对叶轮端面的约束相当于对叶片的弹性约束，加上求解时划分网格的精细程度不同，因此叶片组前2阶的频率和单叶片前2阶的频率差不多或者更低。

表3 动力刚化对叶片组固有频率的影响

图5 叶片组第1，2阶频率随转速的变化Fig.5 Relationship between the natural frequency and rotate speed

图6 前3阶叶片组的振型Fig.6 The first three orders vibration modes of blade group

由图5可以看出，旋转的叶片组也存在动力刚化，对频率的影响随转速的增大而增大，第1阶的频率值随转速变化较快，而第2阶变化较慢，说明惯性力对切向弯曲刚度的影响大于对轴向弯曲刚度的影响，该结论和单个叶片的相同。

图6中转速为0和转速为9kr/min下前3阶的阵型图对比可以看出，转速虽使叶片组产生动力刚化效应，但是其对应的阵型图并没有改变，即第1阶都对应叶片组的切向弯曲振动，第2阶都对应轴向弯曲振动，第3阶都对应扭转振动。同时和单叶片的振型对比可看出，对于叶片组其扭转振动会提前。

3 有限元法求解两个叶片组频率

因为在汽轮机的运行过程中，有时是用一个围带把几个叶片连接在一起形成一个叶片组，这样两个相邻的叶片组之间在运行过程中顶部的围带就会形成碰撞。由于透平运行环境的恶劣，研究这种情况下围带的碰撞和叶片的振动对于解决透平故障很有必要。

在Solidworks中建立6个叶片的模型。进行ANSYS分析时，每3个叶片形成1个叶片组，其顶部的围带采用bonded约束，仍采用solid185和solid285单元划分网格，得到2 260 054个单元。对于两个由3个叶片形成的叶片组顶部围带之间的连接，因为在实际汽轮机围带的碰撞过程中不会发生互相嵌入，为模拟真实的情况，防止两个叶片组大幅度互相嵌入，这里构造了弹簧模型[20]。在两个相邻叶片的围带之间采用6根弹簧连接，根据叶片顶部围带之间实际碰撞情况，赋值弹簧的抗拉刚度K1=10kN/m，扭转刚度K2=120N/m，弹簧的作用是保证顶部围带在相互足够近时弹簧被挤压，在分的足够开时弹簧处于原长。求解的频率如表4所示，振型(因为具有对称性,只列举1，3，5，7阶的振型)如图7所示。

由表4可以看出，第1阶频率和第2阶的频率值很接近，后面每相邻两阶的频率也很接近。这是由于该部分叶轮和叶片形成完全对称的结构，而且从振型图中可以看出它们属于同一类型的振动，如第1阶和第2阶都属于切向弯曲振动，即两个叶片组是交替振动的。由图7可以看出，这种结构的叶片结构仍是以切向弯曲振动和轴向弯曲振动为主要振动形式，而对于扭转振动，要到相对较高阶的振型才会有较显著的表现。

图7 两个叶片组的振型图Fig.7 The mode shape of two blade groups

4 结论

1) 叶片的固有频率和动频率随着阶数增大而逐渐增大，当加上转速后，动频率比静频率大，而且转速越高，惯性力对刚度的影响越大,动频也越大。这与理论分析的离心力增加了叶片的刚性而使动频增加的结论相吻合，即“动力刚化”效应。

2) 对于叶根固定叶顶自由的A型振动，1阶切向弯曲振动(最小惯性轴方向)频率随转速的变化发生较大变化，即对转速的变化较敏感，即离心力的作用使1阶模态刚度矩阵变化较大。

3) 叶片整体振动以弯曲振动为主。当叶片顶部受约束时，其振动频率显著增大。对于A型和B型振动，其最容易发生的都是切向弯曲振动，相比于A型振动，B型振动中的扭转振动的阶次会提前。

4) 旋转叶片组中各叶片变形间相互影响并与叶轮的弹性变形成为一耦合系统，其固有频率相对于各叶片有一定的降低。

5) 在一定转速范围内(本研究在9kr/min以下)，振型图并不会随转速的增加而改变，即转速并没有改变各阶的振型。

[1] 卢晓华,林俊灿.叶根阻尼对叶片振动的影响[J]．上海机械学院学报，1986，8(4):21-32.

Lu Xiaohua, Lin Juncan. The effect of blade root damping on the blade vibration[J]． Journal of Shanghai Institute of Mechanical Engineering, 1986, 8(4):21-32.(in Chinese)

[2] Liu Yongxian, Zhao Weiqiang. Vibration analysis of aero-engine turbine blade-disc coupling system[J]. Applied Mechanics and Materials, 2013, 327:276-279.

[3] Jung H K, Hyun Y P, Seok Y J, et al．Linear vibration analysis of rotaing wind-turbine blade[J]. Current Applied Physics, 2010, 10: 332-334.

[4] Lim H S, Chung J T, Yoo H H. Modal analysis of a rotating multi-packet blade system[J]. Journal of Sound and Vibration, 2009, 325(3)：513-531.

[5] Zhao Weiqiang, Liu Yongxian, Lu Mowu, et al. Vibration analysis of a certain type of aero-engine turbine blade based on UG[C] ∥Informatics in Control, Automation and Robotics. Berlin: Springer Berlin Heidelberg, 2012: 377-382.

[6] Celep Z, Turhan D. On the influence of pre-twisting on the vibration of beams including the shear and rotatory inertia effects[J]．Journal of Sound and Vibration, 1986, l10(3): 523-528．

[7] 刘岩，张军辉．有限元技术在空冷汽轮机长叶片设计中的应用[J]．热力透平，2012, 41(2): 147-151.

Liu Yan, Zhang Junhui. AppIication of FEA for design of long blade in air cooled steam turbine [J]. Thermal Turbine, 2012, 41(2): 147-151.(in Chinese)

[8] Rao J S, Carnegie W. A numerical procedure for the determination of the frequencies and mode shapes of lateral vibration of blades allowing for the effect of pre-twist and rotation[J]. International Journal of Mechanical Engineering Education, 1973, 1(1): 37-47．

[9] 赵永健，张大千．涡轮盘-叶片整体振动固有模态有限元分析[J]．沈阳航空工业学院学报，2005,22 (5)：4-6.

Zhao Yongjian, Zhang Daqian. Finite element analysis on inherent mode of turbine disk-blade[J].Journal of Shenyang Institute of Aeronautical Engineering, 2005, 22(5): 4-6.(in Chinese)

[10]马玉星，李惠彬，王一棣，等. 涡轮增压器叶片振动分析[J]．振动、测试与诊断，2005，25(2): 13l-156.

Ma Yuxing, Li Huibin, Wang Yidi, et al. Study on vibration of turbo-charger blades[J]. Journal of Vibration, Measurement and Diagnosis，2005，25(2)：13l-156.(in Chinese)

[11]马利，解江，续斌，等. 工作环境下的叶片振动可靠性研究[J].汽轮机技术，2007，49(1)：40-42.

Ma Li, Xie Jiang，Xu Bin，et al. Study on blade vibration of reliability under working environment [J]. Turbine Technology, 2007, 49(1): 40-42.(in Chinese)

[12]李春旺,李海云,王澈,等.航空发动机涡轮叶片振动模态影响因素研究[J].空军工程大学：自然科学版，2014，15(1)：5-9.

Li Chunwang, Li Haiyun, Wang Che, et al. A study of influenceing factors on frequencies and mode shapes of aeroengine turbine blades [J]. Journal of Air Force Engineering University:Natural Science Edition,2014, 15(1):5-9.(in Chinese)

[13]孙强,张忠平,柴桥，等. 航空发动机压气机叶片振动频率与温度的关系[J].应用力学学报,2004,21(4):137-139.

Sun Qiang, Zhang Zhongping, Chai Qiao, et al. Temperature effect on vibration frequency of aero-engine compressor blade [J]. Chinese Journal of Applied Mechanic, 2004, 21(4): 137-139.(in Chinese)

[14]Hong Yi, He Xiaodong, Wang Rongguo. Vibration and damping analysis of a composite blad[J]. Materials and Design, 2012, 34:98-105.

[15]吴厚钰.透平零件结构和强度计算[M]. 北京：机械工业出版社，1982:56-106．

[16]胡于进，王璋奇. 有限元分析及应用[M]. 北京：清华大学出版社，2009:154-225.

[17]金在权，权成七，刘龙哲. 弹性旋转梁的动力刚化效应[J].延边大学学报,2000,26(2):116-118.

Jin Zaiquan, Quan Chengqi, Liu Longzhe. The stiffening effect of the centrifugal force[J]. Journal of Yanbian University, 2000, 26(2): 116-118.(in Chinese)

[18]信伟平. 风力机旋转叶片动力特性及响应分析[D]. 汕头:汕头大学，2005.

[19]李德源，叶枝全，包能胜，等. 风力机旋转风轮振动模态分析[J]. 太阳能学报, 2004, 25(1):72-77．

Li Deyuan, Ye Zhiquan, Bao Nengsheng, et al. Vibration modal analysis of the rotating rotor of horizontal axis wind turbine [J]. Acta Energiae Solaris Sinica, 2004, 25(1): 72-77．(in Chinese)

[20]黄文俊. 汽轮机自带围带叶片动力特性有限元分析[D]. 长沙：长沙理工大学，2007.