考虑不同库水耦合模式的拱坝振动特性分析*

2017-01-09张建伟曹克磊刘晓亮暴振磊

振动、测试与诊断 2016年6期

关键词：拱坝坝体模态

张建伟, 曹克磊, 赵瑜, 江琦, 刘晓亮, 暴振磊

(华北水利水电大学水利学院郑州, 450011)

考虑不同库水耦合模式的拱坝振动特性分析*

张建伟, 曹克磊, 赵瑜, 江琦, 刘晓亮, 暴振磊

(华北水利水电大学水利学院郑州, 450011)

为探讨不同库水模型对拱坝结构动力特性的影响，结合拉西瓦工程实例，分别建立附加质量模型与流固耦合(fluid solid interaction, 简称FSI)系统耦合模型进行动力特性分析，并将仿真结果与依据小波阈值-经验模态分解联合滤波的随机子空间(stochastic subspace identification,简称SSI)法辨识结果进行对比。结果表明：两种模型均可反映结构的振动特性，附加质量模型计算结果与辨识结果的频率误差为0.41%～7.55%；FSI系统耦合模型计算结果误差为0.09%～3.19%，且同阶次频率误差均比附加质量模型小，相邻阶次的频率间隔相对稳定，弥补了附加质量模型的模态缺失现象。FSI系统耦合模型在模拟阶数和精度方面都优于附加质量模型，能更全面、准确地反映坝体振动信息，可在拱坝结构动力特性分析中推广应用，亦可作为后续拱坝结构损伤诊断研究的基准有限元模型。

拱坝；附加质量模型；流固耦合系统模型；小波阈值及经验模态分解联合滤波；随机子空间模态辨识

引言

水流诱发坝体振动[1-2]是工程运行期间普遍存在的一种现象，与坝体受到的特殊水力学特性密切相关，因其作用机理复杂，至今尚无完善的理论基础能够彻底解决这一问题。实际研究发现，坝体固有振动特性是导致坝体产生振动的内在因素，且其振动性质和量级主要由结构的固有振动特性和动水荷载效应决定。因此，选用合理的库水模型进行坝体结构的固有振动特性分析是解决水流激振问题的必要前提。

自动水压力Westergaard(韦斯特伽德)公式[3]在1933年被提出以来，流体对结构动力特性的影响问题一直是该领域研究的热点。现阶段常用于建立不同耦合形式库水模型的方法有韦斯特伽德附加质量法、流固耦合法等。韦斯特伽德附加质量法具备动力等效计算简单、易实现且能近似反映工程特性等优点。流固耦合法因能很好拟合出流固两相介质之间相互作用，计算精度高，而被工程和学术研究领域广泛应用。基于不同模拟法的自身优点，大量学者从不同的角度入手进行了一系列研究。陈厚群等[4]结合模型试验结果，分析得出减半取用流体附加质量值的结论。吴一红等[5]分析了拱坝-库水-地基耦合系统作用下地基模拟范围大小对结构固有频率值的影响特性。古华等[6]计算了不同液相长度下闸门结构的固有频率值，揭示了液相长度选取对结构自振特性有较大的影响，实际计算中不能忽略。Nath等[7]对拱坝结构进行动水压力研究表明，库水可压缩性对坝体的动力响应影响不大。中美合作的拱坝激励试验项目[8]也没明确指出动力计算中能否忽略库水可压缩性的影响。杜建国等[9]提出了基于比例边界有限元法(scaled boundary finite element method,简称SBFEM)的库水模型，降低了动力计算的维数，提高了计算精度和效率。王铭明等[10]采用坝体-库水耦合系统模型对不同坝高进行了地震作用下的动力响应计算，并依此得出了考虑多因素影响的Westergaard修正式。

笔者以拉西瓦工程为研究对象，建立不同流体作用形式的拱坝有限元动力模型，对其进行固有振动特性分析，并与实测结果对比，评价出不同动力模型的优劣，为后续研究选取合理的动力计算模型提供理论参考。

1 基本理论

1.1 广义韦斯特伽德附加质量法

韦斯特伽德附加质量法因具备简便、易实现等优点而被各研究领域广泛应用于考虑流固耦合效应的理论计算中，且具有一定的认可度。该方法不考虑水体的可压缩性，并通过附加在结构表面的等效水体质量来模拟水体对结构的惯性作用。计算时动水压力值的大小被假定为随水深增加而逐渐增大。其计算点附加水体质量的公式为

(1)

其中：H为水深；h为计算作用点距离水面的距离；ρ为库水密度。

为了使附加质量模型的计算结果与真实值吻合的更好，同时也减少附加质量法在实际应用中的诸多假设，Claugh[11]对韦斯特伽德附加质量公式进行了推广，推广后公式的适用性更强，能够应用于任意形状的坝面和河谷，且适应地震动力特性分析中各向地震加速度的输入。其计算表达式为

(2)

其中：ρ为库水密度；li为坝面上点i的法线矢量；Ai为该点在坝面上的隶属面积；H为坝前水深；h为计算作用点i距离水面的距离。

1.2 有限元流固耦合模型

建立固-液两介质相互作用的FSI系统库水耦合模型需对库水进行条件假定：a.库水是均质可压缩性流体，且不考虑其旋、黏及热交换作用的影响；b.库水具有小变形且实际流速远小于流体中声传播速度的特点。依据以上假定条件，建立库水运动方程为

(3)

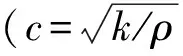
基于FSI系统的库水耦合模型需对边界条件进行如下设定。

1) 在库内水流与坝体上游迎水面接触的交界面Γ1上

(4)

2) 如果库内水体自由表面Γ2上的水面波动效应被忽略，则

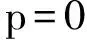
(5)

3) 水库的库水底面Γ3上需满足

(6)

4) 在库内水体的无限远域处，计算时可按无反射条件考虑，令β=1，即

(7)

其中：l为库内水体无限远域处的法向。

水库的动力平衡方程可由Galerkin法离散式(3)～式(7)得出

(8)

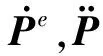
坝体的平衡方程为

(9)

由式(8)、式(9)可得出坝库模型的液-固耦合方程为

(10)

2 工程实例

2.1 工程概况

拉西瓦水电站是龙羊峡至青铜峡流域内国投开发的第二座梯级电站，同时也是黄河上的“五最”电站，其主要枢纽建筑物由双曲拱坝、地下厂房、消能和泄洪建筑物组成。该电站的坝址区位于岸坡陡峭、谷道狭窄的“V”字型地貌处，坝体建在基岩完整性良好、微风化的Ⅱ级花岗岩上。该拱坝坝顶和坝底的最大宽度值分别为10和49m，最大坝高为250m(最大坝高处高程为2 460m)，运行时的兴利蓄水高程为2 452m，水库可调节库容达1.5亿m3。

2.2 有限元建模

依据附加等效水体质量作用理论(广义韦斯特伽德附加质量法)和FSI系统理论，运用ANSYS有限元软件建立不同的结构与水域耦合三维有限元模型(比尺为1∶100)。模型1为库水-坝体-地基为一体的FSI系统模型(见图1)；模型2为附加质量模型(见图2)。由于ANSYS中模拟流固耦合作用时选取单元的特殊性，故两种模型中两岸岩体、基岩及坝体均采用Solid45单元，水体效应则分别选取Fluid30单元和Mass21单元进行模拟。运用Fluid30单元模拟库水影响时水域长度取为6倍的坝高[12-14]，且库底吸收和库水表面重力波的影响[14]忽略不计。坝基基岩模拟范围[5,15]为：水平向沿两岸各延伸2倍坝高；地基深度则沿竖直向取2倍坝高；下游面地基沿流向扩延2倍坝高；附加质量模型上游面地基沿反流向伸长2倍坝高；流固耦合模型中上游面地基延展至与水域长度值一致。模型网格划分采用映射和扫略方法，划分后网格单元为规则的六面体单元，计算中力的传递不易出现应力集中现象，提高了结构的整体计算精度。考虑FSI系统的坝库耦合模型共有单元43 870个，其中坝体单元1 138个，包含耦合层的水体单元18 018个，而附加质量模型包含MASS21单元、坝体和地基共55 666个单元。坝体整体建模选用笛卡尔直角坐标系，顺河向R表示坝体径向振动方向，横河向S表示坝体切向振动方向，竖直向Z表示坝体垂向振动方向。

图2 附加质量拱坝模型Fig.2 Added masses model of arch dam

动力计算中采用的材料参数是由水弹性模型制作过程中所遵循的等容重、等阻尼、等泊松比以及弹模比尺与长度比尺(1∶100)相等的动力学相似准则[16]转化得到。拱坝结构原型动力计算的材料参数为：坝体动弹模值为33GPa；泊松比为0.167；密度为2 400 kg/m3。基岩特性模拟的弹性模量为22GPa；泊松比为0.25；密度为2 700kg/m3。取Rayleigh阻尼的值为0.05，FSI系统模型中水体密度为1 000kg/m3。

2.3 模态计算

有限元数值计算法是进行坝体结构动力特性计算的有效方法之一，能精确求解出反映结构固有动力特性的特征向量和特征值，即结构振型与自振频率，在结构动力计算中被广泛应用。本研究对坝体结构进行动力分析时，针对不同耦合模型选用不同模态提取方法获取结构模态信息：附加质量模型采用高精度、适用范围广、低耗时的分块兰索斯法；FSI系统模型则依据自身耦合振动特性，采用运行程序简单、运算量小、计算精度高的非对称算法(模态提取法的选取主要依据模型大小和具体应用场合)。文中对两种耦合模型在库水高程2 457.0m工况和空库工况进行了模态计算，得出了结构的频率和主振型。限于篇幅仅列出了两种耦合模型的前4阶频率值(见表1)和空库工况的前3阶频率，频率值依次为16.55，20.45和26.13 Hz。由空库和库内有水(水位高程为2 457.0m)工况的计算结果可知：

1) 空库模型自振频率值明显大于库水影响下结构的频率值，说明采用的坝库模型产生了流固耦合效应；

2) 水体与坝体相互作用对坝体结构的自振频率产生一定影响，在结构动力特性分析中不能够忽略，坝体结构的固有频率会随着水位增高而呈依次降低趋势，这主要是因为水位增高会引起整体系统质量矩阵增大。

2.4 模态辨识与验证分析

结合比尺1∶100的拉西瓦加重橡胶水弹性试验模型，如图3所示。其在下游面坝顶拱圈布置11个动位移响应测点(泄洪水位高程为2 457.0m)，测点布置如图4所示。试验采用具有耐冲击的DP型地震式低频振动传感器(DSP-0.35-20-V)，测试工况为表深孔联合泄洪，采样频率为100Hz，采样时间为40s。因拱坝的主振向是径向，切向和垂直向振动相对较小，故仅研究坝体的主振向(R方向)。

图3 拉西瓦水弹性模型Fig.3 Hydro-elastic modelof Laxiwa

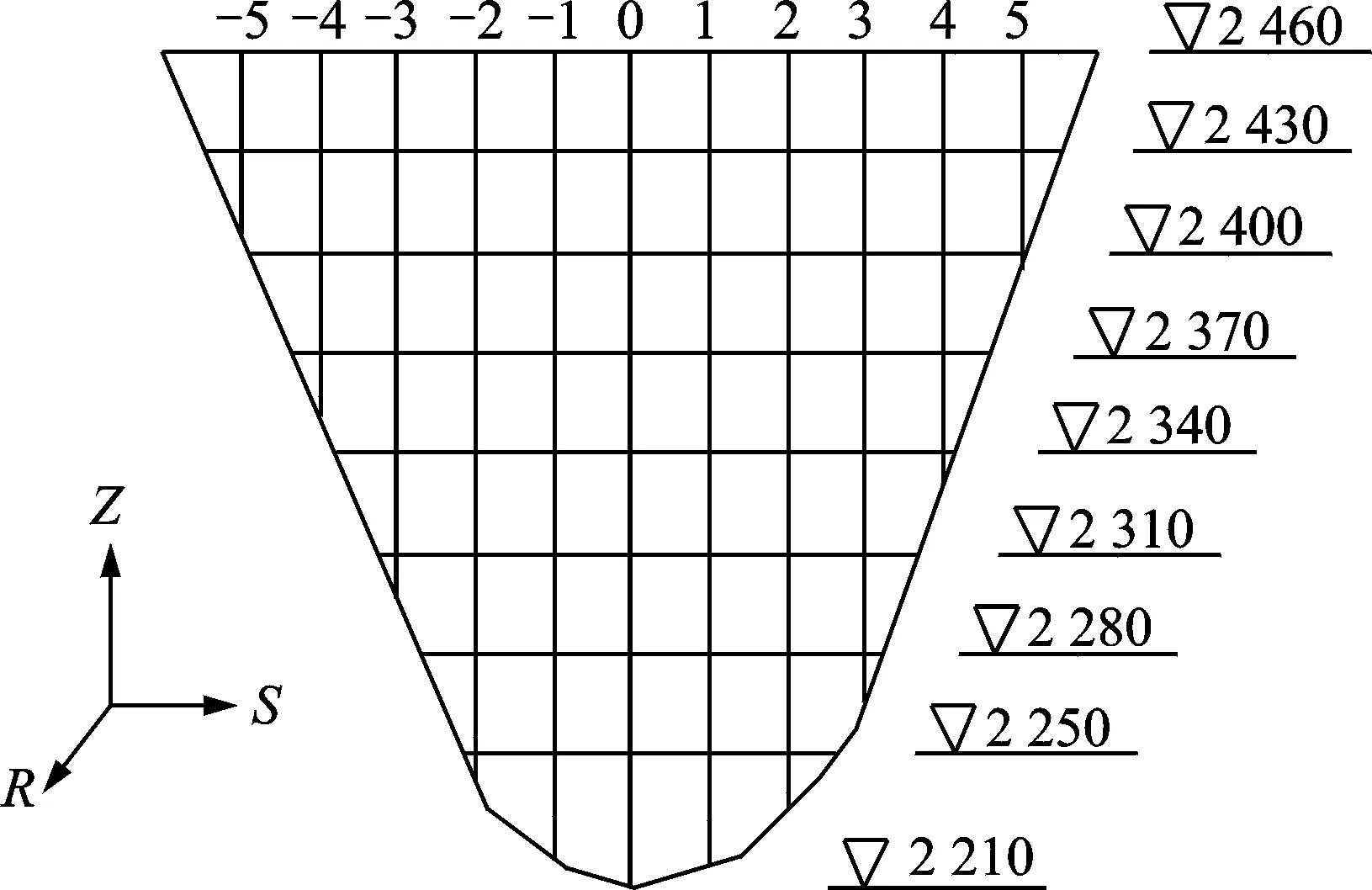
图4 测点布置示意图Fig.4 Arrangement of dobserve points

泄流结构振动信号属于低信噪比信号，结构振动信息往往淹没于低频水流脉动噪声和高频白噪声中。为降低噪声干扰，保证模态辨识精度，采用基于小波阈值与经验模态分解(empirical mode decomposition, 简称EMD)联合滤波[17]的SSI辨识方法[18]。该算法直接作用于时域数据，避免计算协方差矩阵，辨识结果为总体辨识，是目前环境激励下结构模态辨识最为精确的方法之一。

模态参数辨识过程如下。

首先，对11个测点的响应信号进行小波阈值与EMD联合滤波处理，降低背景强噪声干扰，凸显结构振动特性，以振动能量最大的0#测点响应为例说明此滤波过程。根据泄流结构振动特性，选用db5小波，分解层数为4层，滤除信号中的白噪声干扰。经EMD分解得出从高频到低频的9个IMF分量，记为c1～c9。由频谱分析知，c2～c9的主频聚集在10Hz以下，属于典型的受迫振动响应。将c2～c9叠加后得到信号z(t)，对比z(t)与0#测点的原始信号时程和功率谱密度曲线知(见图5)，z(t)能量主要集中在低频部分，是由水流脉冲荷载引起的干扰信息，应当滤除。运用时空滤波器将能够反应坝体振动特性的IMF分量重构得到降噪后信号y(t)，具体降噪过程及参数选取详见文献[17,19]。降噪后信号y(t)频谱图与原始信号对比如图6所示。

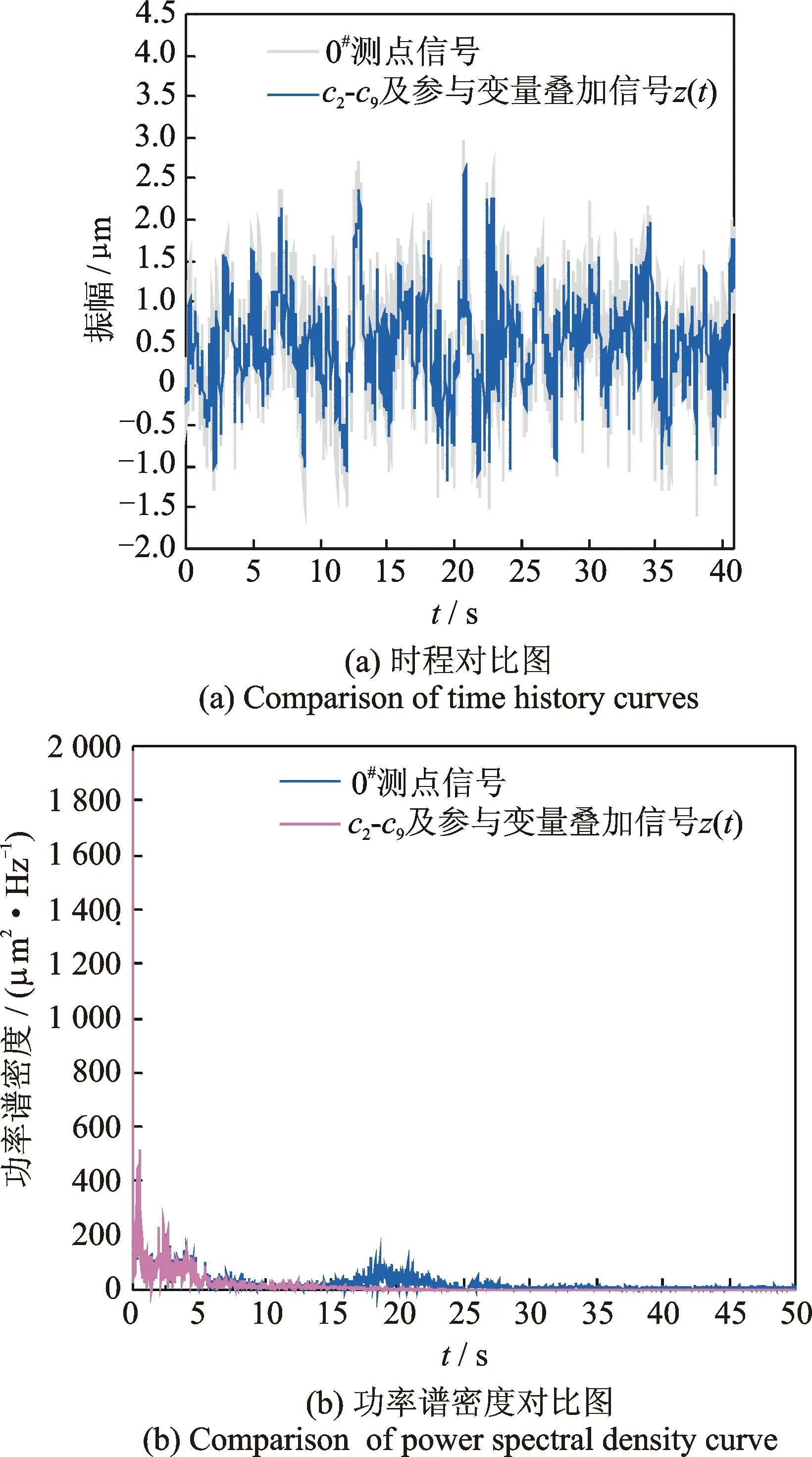
图5 z(t)特征图与0#测点信号特征图比较Fig.5 Comparison of signal characteristic figure for z(t) and measured point 0#

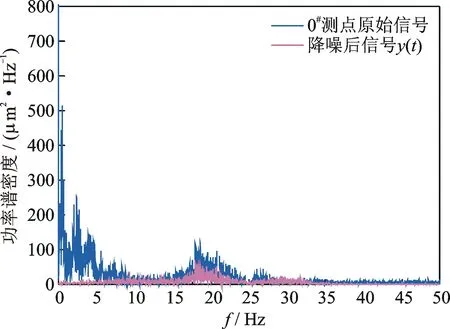
图6 降噪前后频谱图Fig.6 Power spectral density curve of the pre and post de-noising

由图6可知，泄流结构振动信号的高频白噪声和低频水流噪声基本滤除，结构真实振动特性凸显出来。同样，对其他10个测点信号依次按小波阈值与EMD联合方法进行降噪，得到结构振动的有效信息。

图7 频率稳定图Fig.7 Stability diagram of Frequency

由表1可知以下几点。

1) 两种库水模型是以不同耦合形式来反应水体对结构的作用，模拟结果均能较好地与辨识结果吻合，说明采用的库水模型可应用于拱坝结构自振特性分析。

2) 考虑附加质量作用的耦合模型计算结果与模态辨识结果的误差百分比为0.41%～7.55%，而考虑FSI系统耦合模型计算结果与辨识结果的误差百分比为0.09%～3.19%，且同阶次频率误差均比附加质量模型小，误差最大值约为附加质量模型的1/2，相邻阶次的频率间隔相对稳定。对两种模型进行误差分析可知，依据FSI理论建立的耦合模型，计算精度更高，与辨识结果拟合的更好。

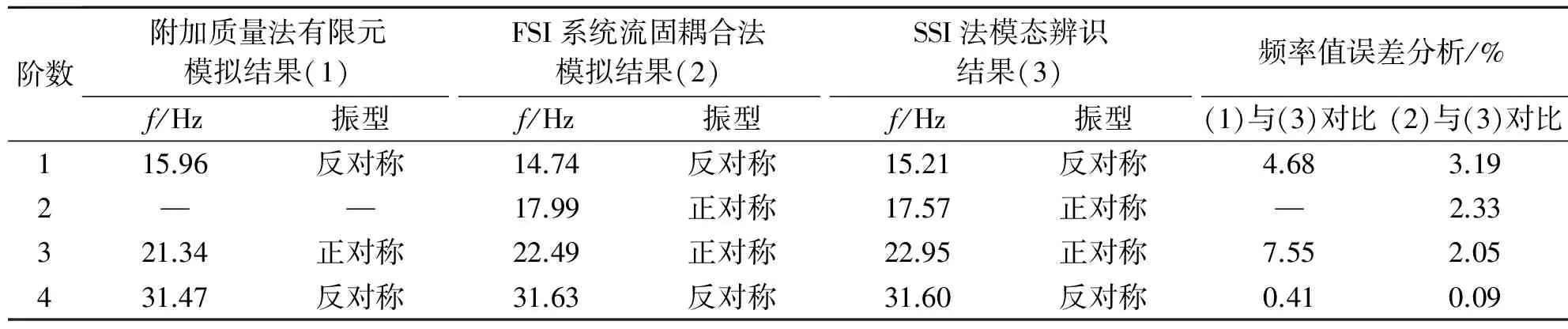
表1 不同耦合模型模拟结果与模态辨识结果对比分析

3) 基于附加质量法的库水耦合模型计算结果出现了低阶模态缺失现象，不能真实全面反应坝体结构的固有特性，对结构健康评估会产生一定影响。该研究中模态缺失现象与文献[21]的规律一致，考虑到篇幅及工程关心的主频问题，仅分析前4阶模态。模态缺失主要是因为附加质量法仅能模拟水体对结构的一阶效应，不能真实反映流-固两相介质之间的相互作用，且得出的各阶固有频率间隔较大，相邻模态重叠较少。

4) 有限元仿真结果与模态辨识结果的相互印证，表明滤波后的模态辨识方法能有效提取结构模态参数，且精度较高。

图8 坝体振型图对比Fig.8 Comparison of dam modal figure

为进一步验证流固耦合模型的优越性，对图8所示的拱坝结构模态辨识及有限元模态计算的振型图进行对比分析。其中，模态辨识振型图中虚线表示拱坝平衡位置，实线表示振型振动位置。

1) 同阶次下基于FSI系统耦合模型算得坝体结构的振型与SSI法辨识出的振型一致，说明所采用的辨识方法与有限元模拟法是合理、有效的。

2) 第1阶与第4阶振型均以坝体中心线为对称轴呈反对称形态；第1阶振型变形最大处在坝体顶部和两侧1/4坝段处，且坝体沿顺河向做反向往复运动；而第4阶振型最大振幅出现在1/4和1/2坝段处。

3) 第2阶与第3阶振型以坝体中心线为对称轴呈正对称形态：第2阶振型振幅呈由坝顶中心向两侧逐渐减小的趋势，坝顶中心处变形最大；而第3阶振幅较大处出现在坝顶中心和两侧1/4坝段处，且两侧1/4坝段处的振幅最大。

3 结论

1) 采用不同模式的库水耦合模型进行拱坝结构固有动力特性分析，并与空库工况、模态辨识结果进行了对比分析。与空库工况结果相比，不同耦合模型的频率值都有较大降幅，说明水体作用对结构的动力特性影响不能忽略。依据FSI理论建立的流固耦合模型，计算精度较附加质量模型高，振型特征与辨识结果一致，频率值误差百分比为0.09%～3.19%，且同阶次频率误差均比附加质量模型小，相邻阶次的频率间隔相对稳定，并弥补了附加质量模型的模态缺失现象。

2) FSI系统耦合模型能更真实、全面反映出拱坝结构的固有振动特性，可作为后续结构损伤诊断研究的基准有限元模型，亦可为结构安全评价奠定基础。

[1] 练继建,马斌,李福田. 高坝流激振动响应的反分析方法[J]. 水利学报,2007,38(5):575-581.

Lian Jijian,Ma Bin,Li Futian. Back analysis algorithm for response of flow-induced vibration in overflow high dam.[J].Journal of Hydraulic Engineering, 2007,38(5):575-581.(in Chinese)

[2] 罗贝尔,王均星,周建烽,等. 基于混沌理论的平板闸门流激振动特性[J]. 振动、测试与诊断,2016,36(1):187-193.

Luo Beier,Wang Junxing,Zhou Jianfeng, et al.Research on the characteristics of flow-induced vibration of bulkhead gate based on chaotic theory.[J]. Journal of Vibration, Measurement & Diagnosis, 2016,36(1):187-193.(in Chinese)

[3] Westergaard H M. Water pressures on dams under earthquakes.[J].Transactions of ASCE, 1933, 98: 418-433.

[4] 陈厚群,侯顺载,杨大伟. 地震条件下拱坝库水相互作用的试验研究[J]. 水利学报, 1989(7): 29-39.

Chen Houqun,Hou Shunzai,Yang Dawei. Study on arch dam-reservoir water interaction under earthquake condition [J]. Journal of Hydraulic Engineering, 1989(7): 29-39.(in Chinese)

[5] 吴一红,李世琴,谢省宗. 拱坝-库水-地基耦合系统坝身泄洪动力分析[J]. 水利学报,1996,11:6-13.

Wu Yihong,Li Shiqing,Xie Shengzong. Dynamic analysis for vibration of dam-water-foundation coupling system during discharge [J]. Journal of Hydraulic Engineering,1996,11:6-13.(in Chinese)

[6] 古华,严根华. 水工闸门流固耦合自振特性数值分析[J]. 振动、测试与诊断,2008,28(3):242-246.

Gu Hua,Yan Genhua. Numerical analysis of natural vibration properties of hydraulic gate considering liquid-solid coupling.[J].Journal of Vibration, Measurement & Diagnosis, 2008,28(3):242-246.(in Chinese)

[7] Nath B, Potamitis S G. Coupled dynamic behavior of realistic arch dams in including hydrodynamic and foundation interaction [J]. ICE Proceedings, 1982, 73(3):587-607.

[8] Clough R W, Chang K T, Chen Hequn, et al. Dynamic interaction effects in arch dams: earthquake engineering research center peport[R].Berkeley:University of California,1985.

[9] 杜建国.基于SBFEM的大坝—库水—地基动力相互作用分析[D].大连：大连理工大学,2007.

[10]王铭明,陈健云,徐强,等. 不同高度重力坝动水压力分析及Westergaard修正公式研究[J]. 工程力学,2013,30(1):65-70.

Wang Mingming,Chen Jianyun, Xu Qiang,et al. Study on different height gravity hydrodynamic pressure and westergaard correction forumla [J].Engineering Mechanics, 2013,30(1):65-70.(in Chinese)

[11]Clough R W. Reservoir interaction effects on the dynamic response of arch dams[C]∥Proceeding of China-US Bilateral Workshop on Earthquake Engineering. Beijing: Water Resource and Hydropower Press of China, 1982: 58-84.

[12]龚亚琦,苏海东,崔建华. 坝体与库水的流固耦合分析[J]. 长江科学院院报,2011,28(6):63-66.

Gong Yaqi,Su Haidong,Cui Jianhua. Fluid-solid coupling analysis of dam-reservoir interaction [J].Journal of Yangtze River Scientific Research Institute, 2011,28(6):63-66.(in Chinese)

[13]王铭明,陈健云,徐强. 重力坝-库水-地基相互作用分析方法比较研究[J]. 大连理工大学学报,2013,53(5):715-722.

Wang Mingming,Chen Jianyun,Xu Qiang. Comparative study of analytical methods of gravity dams-reservoir-foundation interaction [J] Journal of Dalian University of Technology, 2013,53(5):715-722.(in Chinese)

[14]於文欢,任建民,王晓丽. 坝体-库水-地基流固耦合有限元分析的地基模拟[J]. 水电能源科学,2014,32(12):75-77.

Yu Wenhuan,Ren Jianmin,Wang Xiaoli. Dam-reservoir water-foundation of fluid-solid coupling finite element analysis of foundation simulation [J].Water Resources and Power, 2014,32(12):75-77.(in Chinese)

[15]赵兰浩,李同春,牛志伟. 不同库水模型对高拱坝动力特性的影响[J]. 河海大学学报:自然科学版,2009,37(1):48-51.

Zhao Lanhao,Li Tongchun,Niu Zhiwei. Effects of reservoir models on dynamic characteristics of high arch dams[J] Journal of Hohai University:Natural Sciences, 2009,37(1):48-51.(in Chinese)

[16]马斌. 高拱坝及反拱水垫塘结构泄洪安全分析与模拟[D].天津：天津大学,2007.

[17]张建伟,江琦,赵瑜,等. 一种适用于泄流结构振动分析的信号降噪方法[J].振动与冲击,2015,34(20):179-184.

Zhang Jianwei,Jiang Qi,Zhao Yu,et al.De-noising method for vibration signal of flood discharge structure [J]. Journal of Vibration and Shock, 2015,34(20):179-184.(in Chinese)

[18]张建伟,康迎宾,张翌娜,等. 基于泄流响应的高拱坝模态参数辨识与动态监测[J]. 振动与冲击,2010,29(9):146-150.

Zhang Jianwei,Kang Yingbin,Zhang Yina,et al. Modal parameter identification and dynam icmonitoring of high arc dam under vibration response induced by flow discharge [J]. Journal of Vibration and Shock, 2010,29(9):146-150.(in Chinese)

[19]张建伟,朱良欢,江琦,等. 基于HHT的高坝泄流结构工作模态参数辨识[J]. 振动、测试与诊断,2015,35(4):777-783.

Zhang Jianwei,Zhu Lianghuan, Jiang Qi,et al. Research on operating modal parameter identification for high dam discharge structure based on the hilbert-huang transform[J]. Journal of Vibration, Measurement & Diagnosis, 2015,35(4):777-783.(in Chinese)

[20]张建伟,张翌娜,赵瑜. 泄流激励下水工结构应变模态参数时域辨识研究[J]. 水力发电学报,2012,31(3):199-203.

Zhang Jianwei,Zhang Yina,Zhao Yu.Study on strain modal parameters identification of hydraulic structure in time domain under discharge excitations [J]. Journal of Hydroelectric Engineering, 2012,31(3):199-203.(in Chinese)

[21]姬贺炯,白长青,韩省亮. 输流管道动力有限元建模及实验研究[J].应用力学学报,2013,30(3):422-427.

Ji Hejiong Bai Changqing Han Shengliang.Dynamic finite element modeling and experimental research of the fluid-filled pipeline[J].Chinese Journal of Applied Mechanics,2013,30(3):422-427.(in Chinese)