一种多目标传感器优化布置方法及其应用*

2017-01-09李世龙马立元李永军王天辉

振动、测试与诊断 2016年6期

关键词：振型灵敏度测点

李世龙, 马立元, 李永军, 王天辉

(1．军械工程学院导弹工程系石家庄，050003) (2．太原卫星发射中心太原，030027)

一种多目标传感器优化布置方法及其应用*

李世龙1,2, 马立元1, 李永军1, 王天辉1

(1．军械工程学院导弹工程系石家庄，050003) (2．太原卫星发射中心太原，030027)

为解决复杂结构损伤识别中的传感器优化布置问题，以某发射台为研究对象，提出了一种多目标传感器优化布置方法(multi-objective optimum sensor placement,简称MO-OSP)。从结构运动方程出发，推导了同时具有各自由度模态独立性信息、损伤灵敏度信息以及运动能量信息的综合信息矩阵。根据信息熵原理，以协调灵敏度矩阵条件数最小和信息矩阵最大为目标，构造了能够兼顾算法敏感性和鲁棒性的目标函数，进而实现测点优选。采用多个评价准则和损伤识别实例，将所提方法与已有的3种典型传感器优化布置方法进行了对比分析。结果表明，提出的MO-OSP方法能充分满足模态线性独立和损伤敏感性，还具有较强的抗噪声性能，是解决复杂结构损伤识别中传感器优化布置问题的有效方法。

多目标；传感器优化布置；损伤识别；模态参数；发射台

引言

在基于振动测试的复杂结构损伤识别中，实测模态数据的完备性和精确度直接影响着损伤识别结果的好坏，而传感器的优化布置则是模态测试中最重要的一个环节[1]。近年来，国内外学者在传感器优化布置方面开展了广泛研究，并取得了许多重要的研究成果[2]。Kammer等[3]提出的有效独立法(effective independence，简称EI)的核心思想是从所有可能的测点出发，逐个排除对目标模态向量贡献小的测点，从而利用尽可能少的传感器来最大程度获取结构的线性无关信息，实现对模态参数的最佳估计。模态动能法(modal kinetic energy，简称MKE)[4]是根据结构的各阶模态振型绘出相应的模态动能分布图，将传感器布置在模态动能较大的位置上，以提高结构模态测试时的信噪比，便于信号采集和模态参数辨识。

由于有效独立法和模态动能法在实际应用中存在诸多局限性[5]，因此一些学者对其进行了改进。Li等[6]采用正交三角分解计算有效独立系数，解决了传统EI方法计算量过大的缺点。为克服EI方法容易将测点布置在一些振动能量较低的位置上，吴子燕等[7]以单位刚度的模态应变能作为驱动点残差系数对有效独立分布向量进行修正，提出了有效独立-驱动点残差法(effective independence-driving point residue，简称EI-DPR)。程建旗等[8]以测点的频响函数为驱动点留数对有效独立分布向量进行加权，提出一种改进的有效独立法用于传感器优化布置。杨雅勋等[9]将有效独立法和运动能量法相结合，提出一种能量系数-有效独立法(energy coefficient-ffective independence，简称EC-EI)。

以有效独立法和模态动能法为基础，近几年还涌现出了许多基于智能优化算法的传感器优化布置方法，这些方法通常选取模态信息矩阵或模态动能等作为目标函数，对传感器测点进行最优化。文献[10-11]将遗传算法引入了传感器优化布置中。文献[12-13]分别采用贝叶斯算法和猴群算法进行了传感器优化布置研究。随着结构损伤识别的不断发展，对识别精度的要求越来越高。Shi等[14]提出了一种基于损伤灵敏度(damage sensitivity，简称DS)的传感器优化布置方法。刘晖等[15]通过分析Fisher信息阵来确定每个自由度包含损伤信息的多少，并以此来确定最优测点。孙小猛等[16-17]根据 Fisher信息熵原理，提出一种基于损伤可识别性的传感器优化布置方法，但该方法只能应用于简单的平面桁架结构，对复杂结构的损伤识别效果一般。

通过分析国内外现有的传感器优化布置方法可知，这些方法大都是基于单个优化目标进行的，未能同时兼顾观测模态的线性独立性、算法的鲁棒性和对结构损伤的敏感性。笔者认为结构损伤识别中的传感器优化布置方案应同时满足三个方面要求：a.所选自由度应最大程度地包含结构的线性无关信息，以实现对模态参数的最佳估计；b.各测点的振动能量应尽可能大，确保实际测试信号具有较高的信噪比；c.实际测得的模态参数应对结构各位置的损伤比较敏感，满足损伤可识别性的基本要求。因此，有必要发展一种能够协调多个优化目标的传感器优化布置方法，使得在有限的测试条件下，实现对结构不同损伤状况的准确识别。笔者将有效独立法、模态动能法和损伤灵敏度法相结合，提出一种多目标传感器优化布置方法(MO-OSP)。通过多个评价指标以及某发射台的损伤识别实例，与EI,DS和EC-EI进行了对比分析，验证了所提方法的有效性和优越性。

1 多目标优化布置的数学模型

一个具有n自由度动力系统的自由振动方程为

(1)

其中：K和M分别为系统的刚度矩阵和质量矩阵;λi为系统的第i个特征值(模态频率);φi为对应的特征向量(模态振型)。

采用摄动有限元法，假设损伤只引起结构刚度产生扰动，忽略质量及阻尼的变化，则系统的振动方程可描述为

(2)

其中：ΔK,Δλi和Δφi分别为系统刚度、特征值及特征向量的变化值。

忽略高阶项，式(2)可变为

(3)

由于结构的模态振型相互独立，故可将第i阶模态振型的变化量Δφi表示为初始结构各阶振型φr(r=1,2,…,n)的线性组合

(4)

kir表示第r阶振型的振型变化参与系数，包含以下两种情况。

(5)

(6)

将式(6)代入式(4)可得

(7)

2) 当r=i时，kir=0，则结构每个单元刚度的摄动为

(8)

其中：L为结构的单元总数；Kk和ak分别为结构第k个单元的刚度矩阵和刚度损伤系数。

由式(7)和式(8)可得

(9)

其中：Si为第i阶模态对于损伤的灵敏度;δ为结构各单元的损伤向量。

(10)

(11)

由振型叠加法可知，结构出现损伤时的动力响应为

(12)

其中：β=diag{δ,…,δ}为对角阵；q为模态坐标向量。

若定义灵敏度矩阵Γ=(ΦS)，θ=(qβq)T，则式(12)可写为

(13)

在测量噪声影响下，结构的动力响应为

(14)

其中：γ表示方差为σ2的静态高斯白噪声。

(15)

根据式(4)，Fisher信息矩阵可表示为

(16)

如果不考虑各自由度对结构损伤的灵敏度信息，则式(16)退化为

(17)

QΦ即为有效独立法[3]中的Fisher信息矩阵，其只反映了各自由度对目标模态线性无关的贡献程度，不包含结构的损伤灵敏度信息。

如果仅考虑损伤对模态振型的影响，则式(16)退化为

QS=STS

(18)

QS即为Shi等[13]提出的传感器优化模型，其只考虑了损伤灵敏度信息。

笔者构造的信息矩阵QΓ是式(17)和式(18)中两类信息的叠加。

各测试自由度振动能量的大小是传感器优化布置中需要考虑的另一个重要因素。如果将传感器布置在模态动能较小的位置上，该测点的信噪比会较低，不利于参数的准确识别。因此，采用运动能量法对信息矩阵QΓ进行进一步修正。

根据模态应变能的基本原理，结构各节点自由度对MSEi的贡献可表示为

(19)

其中：MSEi为结构第i阶模态应变能；K为结构的整体刚度矩阵；φi为结构第i阶模态振型；n为结构自由度数目；φij为第i阶模态下位于结构第j个自由度的振型值。

由此可得第j个自由度对结构第i阶模态应变能的贡献度为

(20)

基于以上原理，可定义各候选测点的能量系数

(21)

(22)

其中：N为所选取的模态总阶数。

采用上式对灵敏度矩阵Γ进行修正

(23)

修正后的信息矩阵为

(24)

2 传感器优化布置方法

(25)

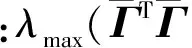
(26)

其中：λmax和λmin分别表示最大和最小特征值。

(27)

由式(25)可得

(28)

由式(26)可得

(29)

(30)

其中：w为权重系数。

(31)

根据式(31)，目标函数可写为

(32)

根据以上原理，对于一个包含n个自由度的结构，若从中选择m个测点，步骤如下：

1) 计算结构的刚度矩阵及振型矩阵；

3) 在所有自由度内循环，删除每个自由度后由式(28)、式(29)和式(31)计算γi1和γi2，并按目标函数f值进行排序，删除使f取最大值对应的自由度；

4) 更新结构的刚度矩阵及振型矩阵，重复步骤2及步骤3，最后剩余的m个自由度即为最终测点位置。

在以上计算中，本研究MO-OSP方法的最大搜索次数为

(33)

采用传统方法的搜索次数为

(34)

对比式(33)和式(34)可以看出，本研究方法的计算次数较传统方法少很多，求解效率更高。

3 实例分析

以某发射台为研究对象，进行传感器优化布置及损伤识别研究。发射台主体为钢管焊接结构，经适当简化，其结构如图1所示。模型共包含24个自由节点、3个固定节点及34个梁单元，每个节点3个自由度，共72个自由度。材料的弹性模量为2.07×1011N/m2，泊松比为0.27，密度为7 800 kg/m3。采用ANSYS软件对其进行有限元建模，计算得到的前5阶模态频率分别为83.92，144.99，285.83，437.36和584.67 Hz。

图1 发射台结构示意图Fig.1 Mechanical structure of the launch platform

3.1 传感器优化布置

为验证笔者所提MO-OSP方法的有效性，分别采用有效独立法(EI)、损伤灵敏度法(DS)、能量系数-有效独立法(EC-EI)以及本研究方法，进行发射台的传感器优化布置研究。利用前5阶计算模态数据，各自由度的有效独立向量和对损伤灵敏度矩阵秩的贡献分别如图2和图3所示；采用EC-EI法计算得到的各自由度的能量系数分布如图4所示。以上均为第1次迭代后的计算结果。从图中可以看出，各个节点、各个自由度对模态独立性和损伤灵敏度矩阵秩的贡献均不相同，不同自由度的能量系数差别也较大。单独采用任何一种方法，将得到截然不同的传感器优化布置结果。

图2 各自由度有效独立向量分布Fig.2 Effective independence vector distribution of each freedom

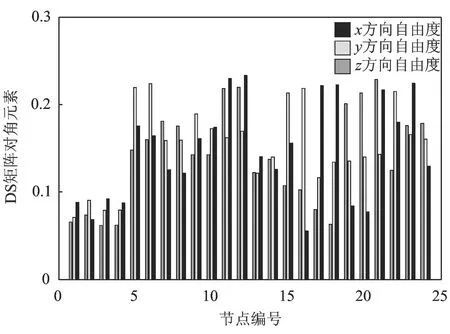
图3 DS矩阵对角元素分布Fig.3 Diagonal terms distribution of each freedom

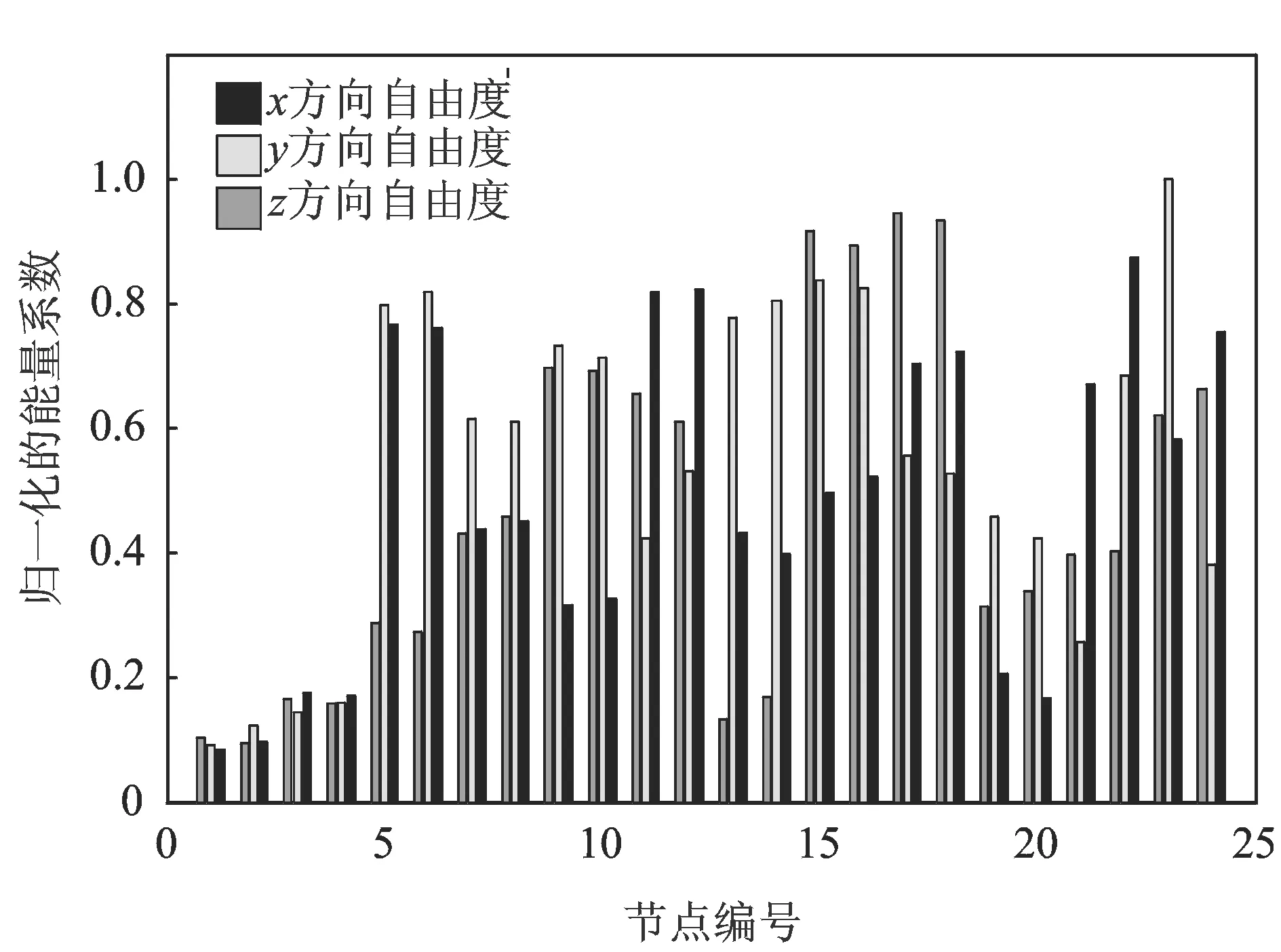
图4 归一化后的各自由度能量系数分布Fig.4 Normalized energy coefficient distribution of each freedom

从结构的72个自由度中选择16个自由度作为测点，4种方法得到的优化布置结果如表1～表4所示。

表1 测点优化布置结果(有效独立法)

表2 测点优化布置结果(损伤灵敏度法)

表3 测点优化布置结果(能量系数-有效独立法)

Tab.3 Optimal sensor placement results (EC-EI method)

节点565611121314方向xxyyxxyy节点1516151617182223方向yyzzzzxy

表4 测点优化布置结果(多目标方法)

Tab.4Optimalsensorplacementresults(MO-OSPmethod)

节点5691011121516方向xxyyzzyy节点1516171821222324方向zzxxzyxx

从表1～表4可以看出，4种方法得到的优化布置结果不尽相同。能量系数-有效独立法确定的测点位置与有效独立法相比，有7个测点发生改变，由原来自由度移动至模态动能较大的自由度上；笔者所提MO-OSP方法确定的测点方案介于有效独立法、损伤灵敏度法以及能量系数-有效独立法之间，既能保证所测模态向量的最大线性独立，又能保证测点的振动能量较大，同时对结构的损伤信息也较敏感。

3.2 优化布置结果评价分析

采用几种通用的传感器优化布置评价指标对4种方法进行分析评价，结果如表5所示。其中前3个指标为相对大小，后2个指标为绝对大小。采用质量归一化振型，量级取10-3。

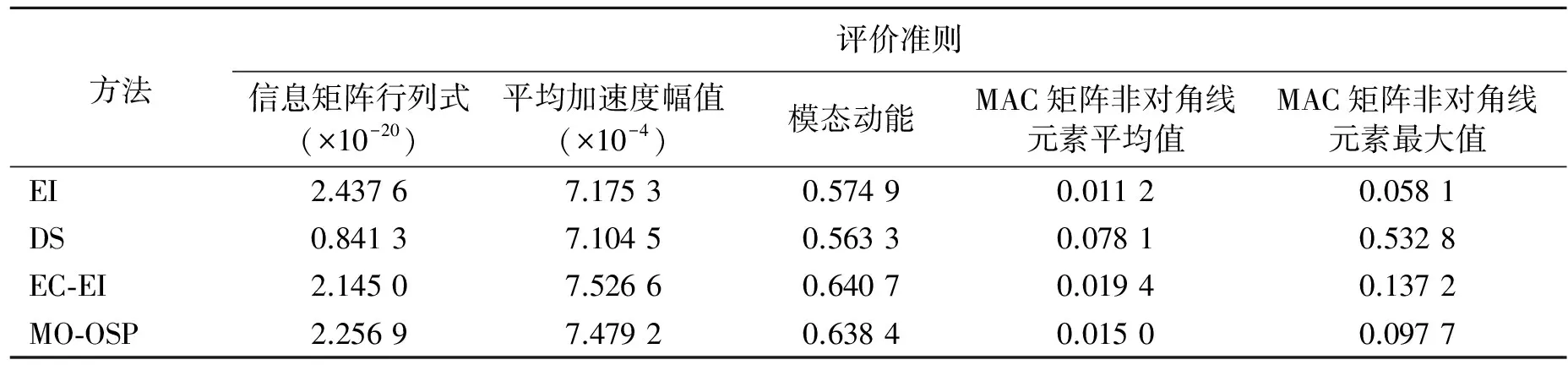
表5 不同评价指标的对比分析

信息矩阵行列式反映了所获模态参数信息量的大小，其值越大，说明目标模态的线性独立性越好。MO-OSP方法的信息矩阵行列式介于DS法和EI法之间，略大于EC-EI法，说明本研究方法在考虑了结构损伤灵敏度信息的同时，还保持了EI法捕获模态信息能力强的优点。

平均加速度幅值和模态动能体现了测点所在位置响应幅值的大小，将传感器设置在响应幅值较大的位置，有利于数据采集并提高算法的抗噪能力。MO-OSP方法的平均加速度幅值和模态动能与EC-EI法基本相同，DS法和EI法的取值相比较小，说明本研究方法较好地考虑了测点的能量信息。

MAC矩阵非对角线元素平均值和最大值是从模态向量线性独立性的角度来评价测点优劣的指标，MO-OSP方法的MAC矩阵非对角线元素略大于EI法，但优于DS法和EC-EI法，具体可参照图5中的MAC矩阵直方图。可以看出，本研究方法的截断模态线性独立性较好。

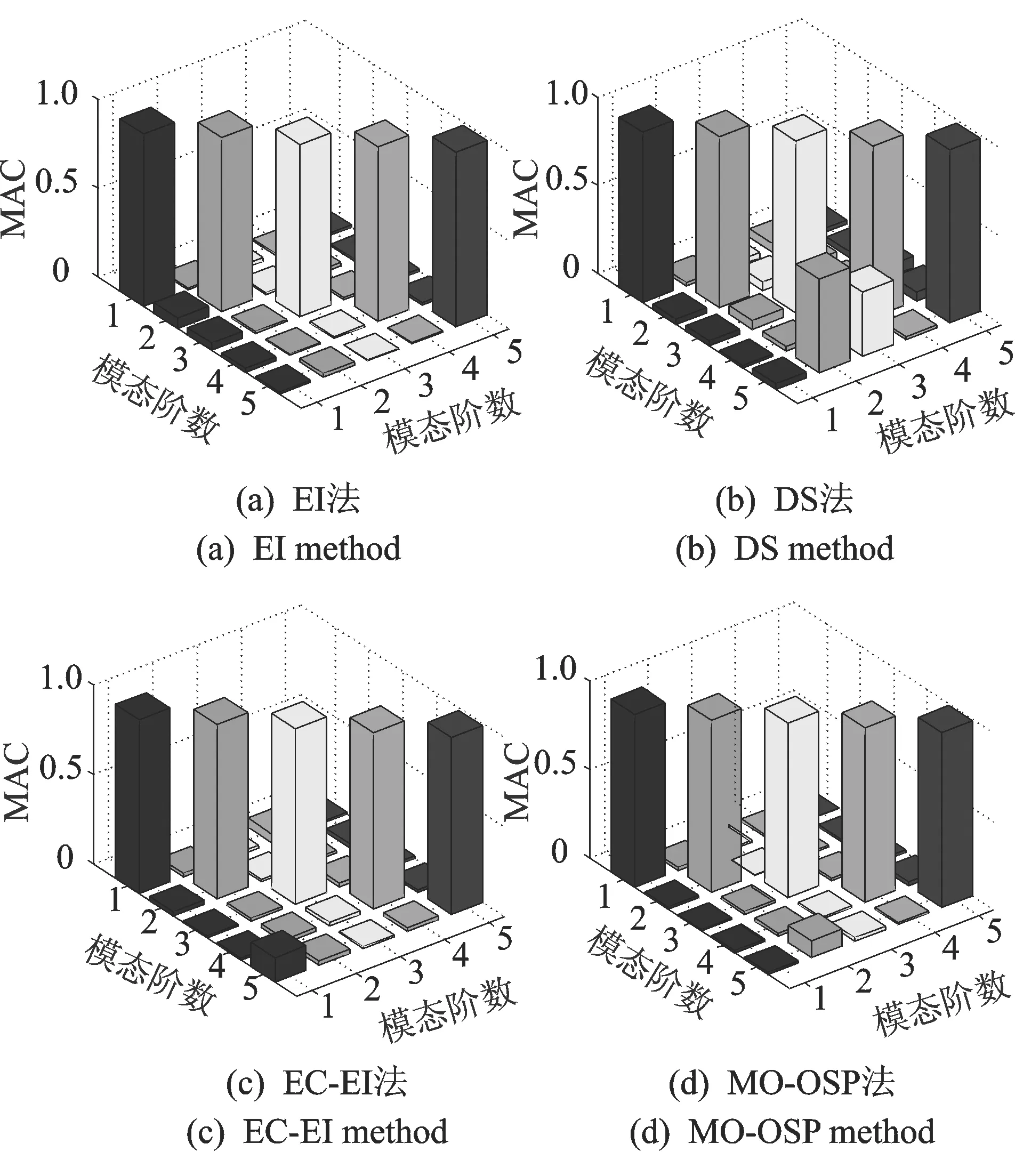
图5 MAC矩阵直方图Fig.5 MAC matrix histogram

3.3 损伤识别分析

利用结构损伤前后的模态频率及模态振型残差，构造损伤识别目标函数如下

(35)

其中：p为待识别单元的刚度损伤因子；E为模态参数残差列阵;ei为E中的第i个值。

(36)

其中：Ef(p)和Eφ(p)分别代表结构的频率和振型残差。

(37)

(38)

其中：上标^为实测模态数据；j为模态阶次。

将发射台按结构特点划分为18个单元组，如图6所示。通过降低单元组的弹性模量来模拟实际损伤，根据表1～表4的测点优化布置结果，从损伤和完好结构的计算模态振型中提取相应自由度的振型信息，采用信赖域优化算法[18]对式(35)进行最小化，从而实现发射台损伤的识别。

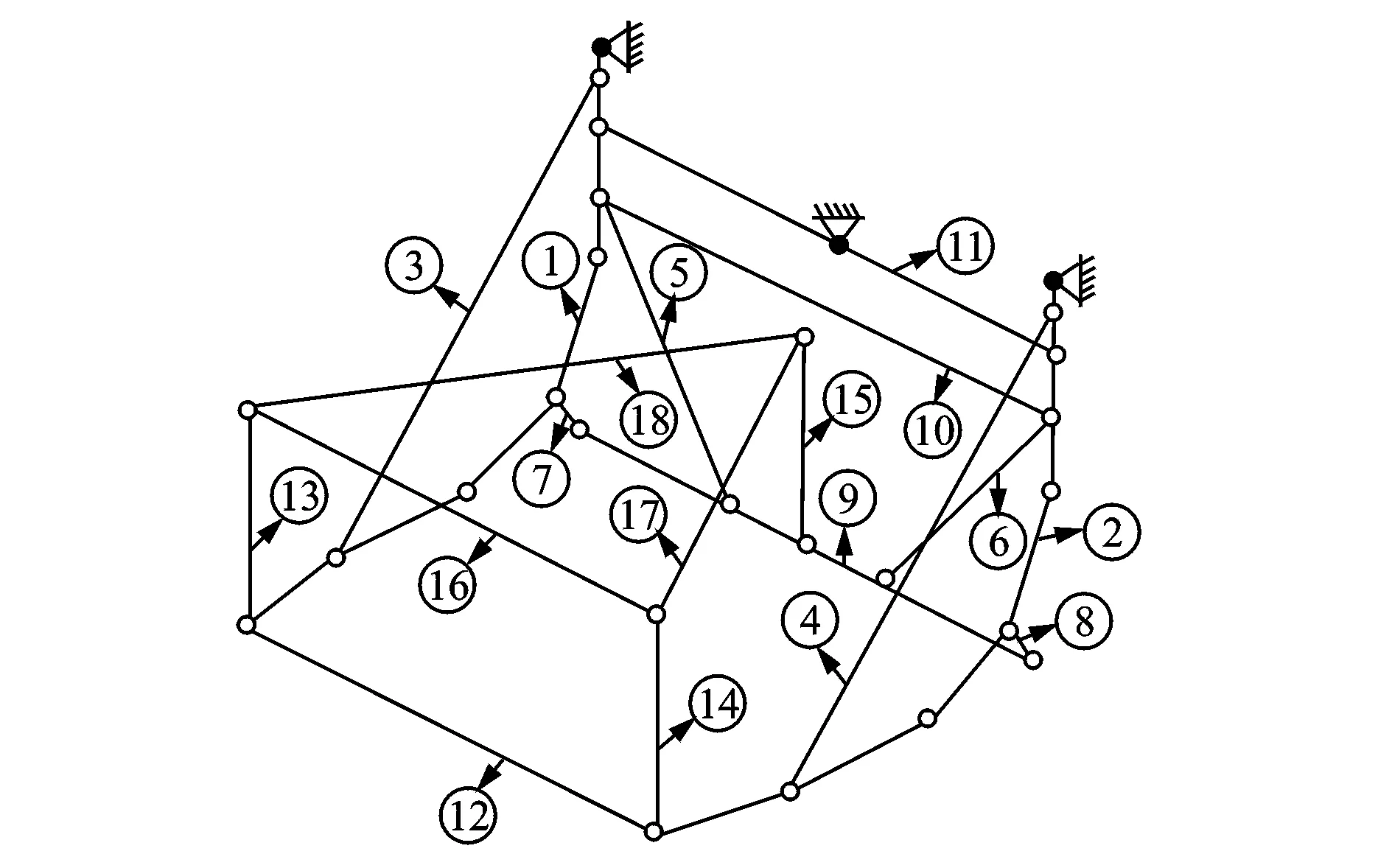
图6 损伤识别单元组分布Fig.6 Distribution of elements group

为充分比较4种传感器优化布置方法在发射台损伤识别中的效果，共设置了3种不同的损伤工况，如表6所示。

表6 损伤工况设置

在无噪声条件下，4种传感器优化布置方案得到的损伤识别结果对比如图7所示。从图7中可以看出:笔者所提MO-OSP方法对3种工况的识别结果均比较准确；EC-EI方法只能准确识别工况1中的损伤，对工况2中7号单元组损伤程度的判断存在较大误差，对工况3中未损伤的7号单元组出现了7.63%的误判，而且对实际损伤的3号和8号单元组损伤程度的判断也不准确；EI方法和DS方法对工况1和工况2损伤程度的判断不够准确，对工况3的识别结果都较差。

在实际模态测试中，测试噪声不可避免，而在测试噪声的影响下，更有利于检验不同传感器布置方案的优劣。因此，本研究在模态频率和模态振型中分别加入了水平为4%和3%的噪声。利用有噪声污染的模态数据，4种传感器优化布置方案得到的损伤识别结果对比如图8所示。

从识别结果可以看出，笔者所提MO-OSP方法在有噪声污染的情况下，依然可以有效识别出结构不同位置、不同程度的损伤；其余3种方法的识别效果非常不理想，对实际损伤单元组损伤程度的识别误差较大，同时还出现了许多误判。

图7 损伤识别结果Fig.7 Damage detection results

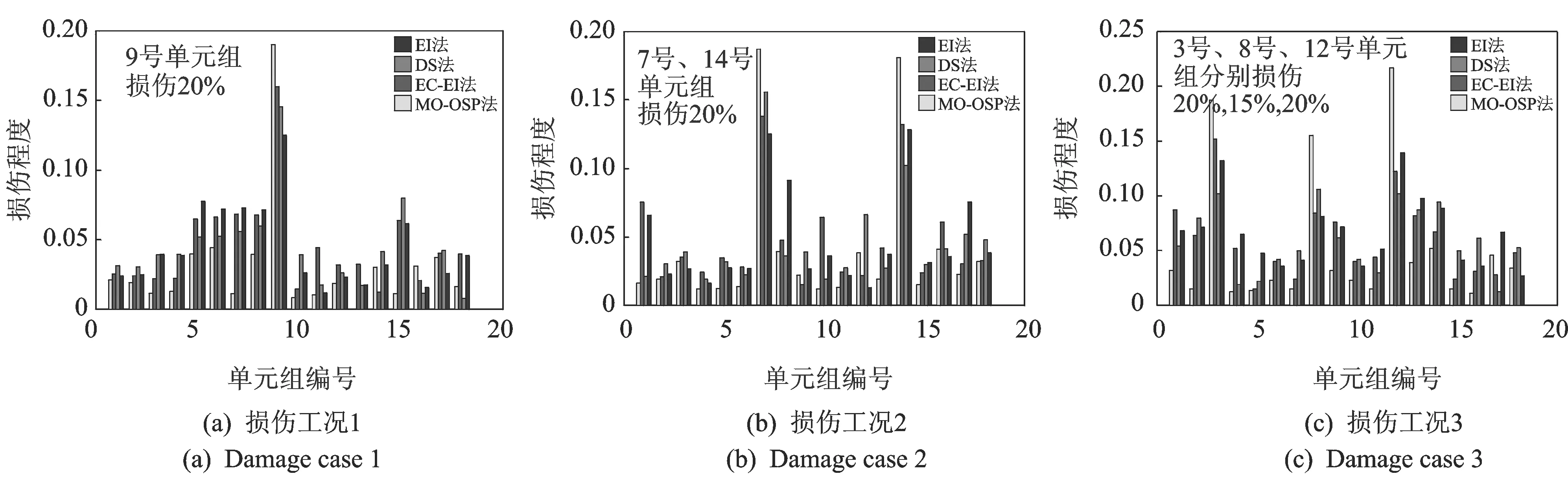
图8 噪声影响下损伤识别结果Fig.8 Damage detection results under noise influence

4 结论

1) 笔者推导的信息矩阵同时包含结构各自由度的模态独立性信息、运动能量信息和损伤灵敏度信息，同时满足了损伤的可识别性和模态的可观测性两种要求。

2) 通过协调信息矩阵最大和灵敏度矩阵条件数最小构造的目标函数，能够保证算法的敏感性和鲁棒性同时达到最优。

3) 多个评价指标及发射台的损伤识别结果表明，与有效独立法、损伤灵敏度法和能量系数-有效独立法相比，笔者提出的多目标传感器优化布置方法综合了几种方法的优点，在无噪声及有噪声条件下均能够取得较好的损伤识别结果。

[1] Li Zhengnong,Tang Jie,Li Qiusheng. Optimal sensor locations for structural vibration measurements[J]. Applied Acoustics, 2004,65:807-818.

[2] 赵俊, 聂振华, 马宏伟. 拱结构模态测试中传感器优化配置[J]. 振动、测试与诊断, 2011,31(2):217-223.

Zhao Jun, Nie Zhenhua, Ma Hongwei. Sensor placement optimization for modal test of arch structure [J].Journal of Vibration, Measurement & Diagnosis,2011,31(2):217-223.(in Chinese)

[3] Kammer D C,Tinker M L. Optimal placement of triaxial accelerometers for modal vibrate tests [J]. Mechanical Systems and Signal Processing, 2004,18:29-41.

[4] Papadopoulos M，Garcia E. Sensor placement methodologies for dynamic testing [J]. AIAA Journal, 1998,36(2):256-263.

[5] 刘伟, 高维成, 李惠，等. 基于有效独立的改进传感器优化布置方法研究[J]. 振动与冲击, 2013,32(6):54-62.

Liu Wei, Gao Weicheng, Li Hui,et al. Improved optimal sensor placement methods based on effective independence [J]. Journal of Vibration and Shock, 2013,32(6):54-62. (in Chinese)

[6] Li Dongsheng，Li Hongnan，Fritzen C P. A note on fast computation of effective independence through QR downdating for sensor placement [J]. Mechanical Systems and Signal Processing, 2009,23:1160-1168.

[7] 吴子燕，代凤娟，宋静. 损伤检测中的传感器优化布置方法研究[J].西北工业大学学报,2007,25(4):503-507.

Wu Ziyan, Dai Fengjuan，Song Jing. A more efficient optimal sensor placement method for structure damage detection[J].Journal of Northwestern Polytechnical University,2007,25(4):503-507.(in Chinese)

[8] 程建旗, 闫维明, 陈彦江,等. 传感器优化布置的改进有效独立算法[J]. 振动、测试与诊断, 2012,32(5):812-817.

Cheng Jianqi, Yan Weiming, Cheng Yanjiang,et al. Optimal sensor placement for bridge structure based on improved effective independence [J]. Journal of Vibration, Measurement & Diagnosis, 2012,32(5):812-817. (in Chinese)

[9] 杨雅勋, 郝宪武, 孙磊. 基于能量系数-有效独立法的桥梁结构传感器优化布置[J]. 振动与冲击, 2010,29(11):119-124.

Yang Yaxun Hao Xianwu, Sun Lei. Optimal placement of sensors for a bridge structure based on energy coefficient- effective independence method [J]. Journal of Vibration and Shock, 2010,29(11):119-124. (in Chinese)

[10]Guo Shuxiang, Zhang Ling. Optimal placement of sensors for structural health monitoring using improved genetic algorithms [J]. Smart Mater Structure, 2004,13(3):528-534.

[11]滕军, 朱焰煌. 大跨空间钢结构模态参数测试传感器优化布置[J].工程力学, 2011,28(3):150-156.

Teng Jun, Zhu Yanhuang. Optimal sensor placement for modal parameters test of large span spatial steel structural [J].Engineering Mechanics,2011,28(3):150-156. (in Chinese)

[12]Flynn E B, Todd M D. A Bayesian approach to optimal sensor placement for structural health monitoring with application to active sensing [J]. Mechanical Systems and Signal Processing, 2010,24(4):891-903.

[13]伊廷华, 张旭东, 李宏男. 基于分布式猴群算法的传感器优化布置方法研究[J]. 工程力学, 2014,31(3):93-80.

Yi Tinghua, Zhang Xudong, Li Hongnan. Distributed monkey algorithm for optimal sensor placement [J]. Engineering Mechanics,2014,31(3):93-80.(in Chinese)

[14]Shi Z Y,Law S. Optimizing sensor placement for structural damage detection [J]. Journal of Engineering Machines, ASCE, 2000, 126(11):1173-1179.

[15]刘晖, 瞿伟廉, 袁润章. 基于灵敏度分析的结构损伤识别中的传感器优化布置[J]. 地震工程与工程振动, 2003,23(6):85-90.

Liu Hui, Qu Weilian, Yuan Runzhang. Optimal sensor placement for structural damage detection based on sensitivity study[J]. Earthquake Engineering and Engineering Vibration, 2003,23(6):85-90.(in Chinese)

[16]孙小猛, 冯新, 周晶. 基于损伤可识别性的传感器优化布置方法[J]. 大连理工大学学报, 2010,50(2):264-270.

Sun Xiaomeng, Fen Xin, Zhou Jing. A method for optimum sensor placement based on damage identifiability[J].Journal of Dalian University of Technology, 2010,50(2):264-270. (in Chinese)

[17]孙小猛. 基于模态观测的结构健康监测的传感器优化布置方法研究[D].大连:大连理工大学, 2008.

[18]李世龙, 马立元, 田海雷,等. 基于不完备实测模态数据的结构损伤识别方法研究[J]. 振动与冲击, 2014,34(3):196-203.

Li Shilong, Ma Liyuan, Tian Hailei,et al. Structural damage detection method using incomplete measured modal data[J]. Journal of Vibration and Shock, 2014,34(3):196-203. (in Chinese)