自适应邻域构造流形学习算法及故障降维诊断*

2017-01-09张晓涛唐力伟邓士杰

振动、测试与诊断 2016年6期

关键词：构造方法流形降维

张晓涛，唐力伟，王平，邓士杰

(军械工程学院火炮工程系石家庄，050003)

自适应邻域构造流形学习算法及故障降维诊断*

张晓涛，唐力伟，王平，邓士杰

(军械工程学院火炮工程系石家庄，050003)

针对流形学习算法中近邻构造问题，提出一种自适应邻域构造方法，该方法基于马氏距离计算样本间相似系数，由相似系数均值确定初始近邻数，根据样本高斯核概率密度估计调整近邻数，并将自适应邻域构造方法用于改进的主成分分析联合局部保持投景(principal component analysis-locality preserving projections,简称PCA-LPP)流形学习算法中。通过齿轮箱故障类型识别对其特征降维性能进行验证，结果表明，自适应邻域PCA-LPP方法比传统的k近邻方法及原始无处理的特征识别率都高，可以达到94.67%。

自适应；邻域；高斯核概率估计；流形学习；故障诊断

引言

流形学习算法是一类非常有效的非线性数据降维算法[1]，在很多具体的流形学习算法实现中，诸如局部保持投影(locality preserving projection, 简称LPP)[2]、拉普拉斯映射(Laplacian eigenmap,简称LE)[3]都需要先构造数据样本近邻图。传统的近邻图构造主要是k近邻和ε近邻两种方法[4]，其主要缺点在于各个样本的近邻数需要人为经验确定，且所有样本采用相同的近邻数，不能针对样本自身的邻域分布情况进行数据调整。自适应邻域的思想主要是基于样本周围一定范围数据分布的情况，按照预设规则自动确定邻域大小。目前常用的自适应邻域构造思想主要基于欧氏距离或者余弦夹角距离计算相似系数，并根据相似系数的分布设定阈值自适应求取近邻数，这样的方法多用于图像处理及人脸识别研究中。Yang等[5]基于欧氏距离指数函数计算样本相似系数。刘凤连等[6]基于图像欧氏距离导数计算样本相似系数。黄璞等[7]采用样本夹角余弦距离作为相似系数。三种方法在人脸识别研究中取得了良好的分类效果。李城梁等[8]将基于样本切空间距离的自适应邻域方法应用于机械故障信号特征提取，故障分类正确率得到明显提升。

自适应邻域构造方法能够有效避免人为选择近邻范围的随意性，具有更好的样本局部非线性流形特征表达能力。笔者提出一种自适应邻域构造方法，基于马氏距离相似系数均值及样本高斯核概率密度估计调整自适应获得样本近邻数，并将自适应邻域构造方法应用于PCA-LPP流形学习算法，通过齿轮箱故障信号特征向量降维识别验证了自适应邻域PCA-LPP方法的有效性。

1 自适应邻域构造方法

设高维空间RD中存在数据集X=[x1,x2,…,xN]，基于近邻图构造相似矩阵S能够用于多种流形学习算法，实现数据的降维处理。

传统的k近邻构造方法，基于样本间的欧氏距离计算样本相似性，每个样本近邻值相同，相似系数具体表达如下

(1)

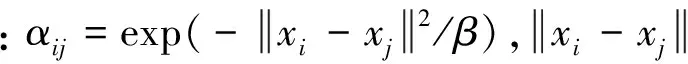
k近邻法存在两点不足：a.所有样本采用相同的近邻数，不能很好地适应每个样本的局部流形结构特征；b.近邻数的选择没有成熟的算法，常使用的交叉验证方法存在效率低下等弊端。

1.1 马氏距离相似度衡量

马氏距离是一种基于数据协方差的距离描述，其定义为

(2)

其中:C为数据集X的协方差矩阵。

马氏距离对一切非奇异性线性变换具有不变性，不受特征量纲选择的影响。马氏距离与欧氏距离的对比如图1所示，图中虚线圆为欧氏距离等距线，实线椭圆为马氏距离等距线。由图1可以看出，马氏距离的描述更符合数据真实的分布情况，仅当协方差矩阵C为单位矩阵时，马氏距离与欧氏距离才会相等[9]。

图1 马氏距离与欧氏距离Fig.1 Mahalanobis distance and Euclidean distance

基于马氏距离数据分布特征描述方面的优势，提出基于马氏距离的样本相似矩阵构造方法，相似矩阵元素表达如下

(3)

其中：αij=exp(-dij/β)；β为所有样本之间马氏距离均值的平方。

1.2 核密度估计调整

样本近邻构造时，空间中密集分布的样本局部特征往往较为相似。对样本xi来讲，其附近区域其他样本出现的概率密度越大，表示与其具有相似局部特征的样本越多，则xi对应的样本近邻数应该大一些。据此提出将高斯核密度估计(Gauss kernel density estimation，简称GKDE)[10]用于近邻图构造，对基于相似系数均值Mi的自适应近邻结果进行修正调整。

高斯核密度估计是一种非参数概率密度估计方法，能够在样本分布先验知识未知的情况下，根据样本自身信息估计总体分布概率密度。高维空间RD中样本xi的邻域概率密度高斯核估计为

(4)

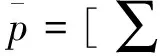
(5)

其中：floor表示数据向负无穷大方向取整。

通过式(5)可知，当xi附近数据样本分布密度大时，该点的近邻数自动调整增大，当其附近数据分布稀疏时，近邻数自动调整减小。

1.3 自适应邻域构造流程及特性

图2 自适应邻域构造流程Fig.2 Flow chart of adaptive neighborhood selection

自适应邻域构造方法最终得到的相似矩阵S一般情况下是非对称的,主要包含以下几种情况：

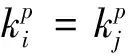
2) 与第1假设相同，当样本xi和xj互相不为近邻时，相似系数αij=αji=0，相似矩阵S对称;

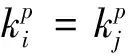
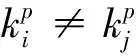
自适应邻域构造方法与传统k近邻方法都是为了表达数据样本局部结构的相似性，主要不同为:

1) k近邻方法基于欧氏距离计算样本相似系数，自适应邻域构造方法基于马氏距离计算相似系数，能够更好地考虑样本分布特性；

2) k近邻方法所有样本近邻数需人为设置，自适应近邻构造方法根据相似系数均值Mi确定样本初始近邻数，并采用样本分布概率密度调整近邻数；

3) k近邻方法所有样本近邻数均相等，自适应近邻构造方法每个样本的近邻数不一定相等，且一般都不相等；

4) k近邻方法得到的相似矩阵S是对称的，自适应近邻构造方法得到的相似矩阵S一般不对称。

1.4 自适应邻域构造实例

采用26个随机二维数据样本，说明自适应邻域构造方法的特点。采用自适应邻域构造方法寻找样本近邻，以样本点A(1,4)和点B(8.5,5)的近邻求解进行说明，并给出k近邻方法的对比，设定k=8。表1为自适应近邻求解过程中的参数及结果。图3中4幅图所示为原始26个样本点及点A和点B的3种近邻求解结果。

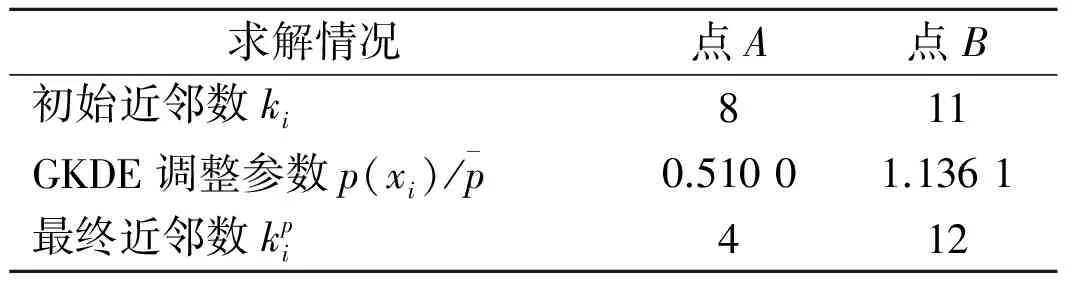
表1 近邻求解参数及结果

图3 点A和点B近邻结果分布Fig.3 Neighborhood for point A and point B

2 自适应邻域PCA-LPP流形学习算法

自适应邻域构造方法能够用于多种基于近邻图构造的流形学习算法，笔者将其应用于一种结合主元分析与局部保持投影的PCA-LPP改进流形学习算法中，标准局部保持投影算法中相似矩阵S为对称矩阵，其对称性对算法的求解带来很大便利。但自适应邻域构造方法得到的相似矩阵S一般为非对称矩阵，其在PCA-LPP中的求解推导如下。

PCA-LPP流形学习目的在于将高维空间RD中的数据集X=[x1,x2,…,xN]，通过投影矩阵W转换投影到低维投影空间Rd(d

PCA方法寻找数据分布方差最大的坐标系，其全局目标函数为

(6)

LPP是一种非线性局部流形保持投影算法，能够保持投影前后数据样本间的局部结构相似，其局部目标函数为

(7)

其中：L′为拉普拉斯矩阵；Dii和Djj为对角阵，其元素为Dii=∑jsij，Djj=∑isij；D′=Dii+Djj;S′=S+ST;sij为相似系数，构成相似矩阵S;W为投影矩阵。

PCA-LPP流形学习算法兼顾PCA的全局分布方差最大特性及LPP的局部流形保持特性，能够全面刻画数据的整体和局部特征，其全局目标函数为

(8)

其中：限定条件WTXD′XTW=I可消除随机尺度因子的影响。

在LPP局部目标函数中，自适应邻域构造方法得到的相似矩阵S是非对称矩阵，但局部目标函数Jl(W)中的矩阵L′是对称矩阵，其证明如下。

证明： ∀ 相似矩阵S

∵ Dii=∑jsij，Djj=∑isij均为对角阵

∴ Dii和Djj为对称矩阵

∴ D′=Dii+Djj,S′=S+ST为对角对称矩阵

∴ L′=D′-S′为对称矩阵。

自适应邻域构造PCA-LPP算法的目标函数式(8)可以通过拉格朗日乘子法[11]，将其转化为有约束最大值问题，如式(9)所示

(9)

式(9)对W求导并置零可得

(10)

化简式(10)可以得到

(C-XL′XT)W=λXD′XTW

(11)

由式(11)可知，投影矩阵W的求解，实质是广义特征值求解问题，通过求取前d个最大特征值对应的特征向量，从而得到投影矩阵W，投影后低维数据通过Y=WTX计算。

由此可以得到自适应邻域PCA-LPP流形学习算法流程,如图4所示。

图4 自适应邻域PCA-LPP算法流程Fig.4 PCA-LPP algorithm based on adaptive neighborhood

3 齿轮箱故障特征降维分析

流形学习算法在数据可视化以及故障特征降维识别中应用广泛[12-13]，下面对自适应邻域PCA-LPP流形学习算法的性能进行验证。

采用齿轮箱故障实测声发射信号对PCA-LPP的特征降维性能进行验证。试验中齿轮箱故障包括正常状态、轴承内圈故障、外圈故障、内外圈复合故障及齿根裂纹故障5种模式，故障轴承为6206，安装在中间传动轴，故障齿轮为中间传动轴大齿轮，一级传动比为0.5，齿轮箱结构原理及传感器安装如图5所示。试验中齿轮箱空负载运转，其输入轴转速为1 490 r/min。信号采集设备为北京软岛DS2-8A型全息声发射信号分析仪，设置采集仪采样频率为1 MHz，采集仪硬件滤波参数为100 kHz～400 kHz带通滤波，声发射传感器为声华SR150M型，匹配40 dB前置放大器。每个数据样本长度为1 s，每种故障模式对应70个样本，5种模式共350个样本。

对每个故障信号样本进行db4小波包4层分解，重构各子频带小波包系数，得到16个子频带重构分量，各子频带宽度为31.25 kHz，计算子频带信号能量，得到能量特征向量E=[E1，E2，…，E16]，求取16个子频带信号的能量熵作为特征向量[8]，能量熵的计算方法如下。

(12)

采用自适应邻域PCA-LPP方法对所提故障特征向量进行处理，并将降维后特征向量输入支持向量机进行训练识别，对比故障模式的分类识别性能，每个故障70个样本中，40个用于训练支持向量机分类器，30个用于样本故障分类识别。

3.1 自适应邻域PCA-LPP故障特征降维识别分析齿轮箱故障声发射信号的特征向量原始维度为16维，采用自适应邻域PCA-LPP对故障特征向量进行降维处理，降维后特征的维度范围为3～15维，间隔为1。不同降维数的特征向量输入支持向量机的整体故障识别率如图6所示。由图6可以看到，原始的16维特征向量经降维处理，不同维度的特征向量对应的故障辨识率有所不同。辨识率在5维以后出现明显增高，当降维数d=8时，整体故障辨识率最高，达到94.67%。其中整体故障辨识率指各单项故障识别率的均值，表示4种故障类型正确识别的总数占150个测试样本的比例。

降维数d=8时，不同故障的辨识率如表2所示。由表2可知，各类故障模式中，齿根裂纹辨识率最高，因为齿根裂纹与其他几种故障具有明显不同，而复合故障辨识率最低，因为复合故障与内、外圈故障具有相似特征成分。

图6 不同降维数的故障识别率Fig.6 Fault identification rate of different dimensions

故障类型齿根裂纹正常状态内圈故障外圈故障复合故障整体识别率%10096．6793．3393．3390．0094．67

3.2 不同识别方法性能对比

对文中的故障特征向量，将k近邻PCA-LPP方法降维识别结果、基于欧氏距离的自适应PCA-LPP方法降维识别结果以及原始特征向量不做任何处理的识别结果与3.1节的识别结果进行对比，k近邻方法的最优识别结果通过交叉验证获得。设置近邻值k的变换范围为5～30，间隔为1，降维数d的范围为3～15，间隔为1，计算后得到k近邻方法在k=17，d=7时获得最高识别率。基于欧氏距离的自适应PCA-LPP方法降维识别在降维数d=8时取得最高识别率。4种方法的识别率对比如表3所示。

表3 3种情况识别率对比

从表3可以看到，原始16维特征向量，不经任何处理，直接进行支持向量机分类器的训练和识别，其故障识别率最低，仅为53.33%，而采用流形学习算法降维之后，故障识别率明显提升。对于同样的PCA-LPP流形学习算法，不同的邻域构造方法带来的降维效果差异较大。自适应邻域构造方法降维后特征的故障识别率可达94.67%，而k近邻方法降维后特征的故障识别率为86.67%。不同相似度衡量方法带来的降维效果也不同，基于马氏距离的相似度衡量最终故障识别率为94.67%，而基于欧氏距离的相似度衡量最终识别率却为88.67%。原始特征向量维度高，其中包含故障特征的差异信息，但高维度同时包含过多的冗余信息，因此其故障识别率低。k近邻方法对所有样本采用相同的近邻数，对各样本局部邻域的描述不能做到分而划之，基于欧氏距离的相似度衡量，对数据样本的分布情况不能充分考虑，因此两种方法特征向量的降维效果不如自适应邻域构造方法，故其故障识别率低于自适应邻域PCA-LPP方法。

4 结束语

针对流形学习算法中近邻图的构造问题，提出一种基于马氏距离的相似矩阵元素计算。根据相似矩阵元素均值确定初始邻域数，并由数据样本邻域高斯核概率密度估计结果调整样本近邻数，解决了自适应构造近邻图的问题。将自适应邻域构造方法应用于兼顾PCA与LPP二者特性的改进流形学习算法，并给出相应的理论计算模型，证明了求解拉普拉斯矩阵的对称性。通过齿轮箱故障声发射信号16维能量熵特征的降维识别对自适应邻域PCA-LPP流形学习算法的性能进行验证，结果表明故障特征降到8维时识别率最高，可以达到94.67%。对比研究表明，自适应邻域构造PCA-LPP方法的降维识别性能优于k近邻PCA-LPP方法以及原始特征向量的识别率。

[1] 赵振华，郝晓弘. 局部保持鉴别投影及其在人脸识别中的应用[J]. 电子与信息学报， 2013，35(2):463-466.

Zhao Zhenhua, Hao Xiaohong. Linear locality preserving and discriminating projection for face recognition[J]. Journal of Electronics & Information Technology， 2013，35(2): 463-466.(in Chinese)

[2] He Xiaofei, Niyogi P. Locality preserving projections[C]∥Neural Information Processing Systems16. Cambridge,USA: MIT Press, 2004：153-160.

[3] 许庆诚，胡建中. 基于改进增量LE的压缩机故障特征提取方法[J]. 仪器仪表学报，2013，34(4):791-796.

Xu Qingcheng, Hu Jianzhong. Fault feature extraction method for compressor based on improved incremental Laplacian eigenmap algorithm[J]. Chinese Journal of Scientific Instrument， 2013，34(4):791-796.(in Chinese)

[4] 何强，蔡洪，韩壮志，等. 基于非线性流形学习的ISAR目标识别研究[J]. 电子学报， 2010,38(3):585-590.

He Qiang, Cai Hong, Han Zhuangzhi, et al. ISAR target recognition based on non-linear manifold learning[J]. Acta Electronica Sinica，2010，38(3):585-590.(in Chinese)

[5] Yang Bo, Chen Songcan. Sample-dependent graph construction with application to dimensionality reduction[J]. Neurocomputing， 2010，74(5): 301-314.

[6] 刘凤连，汪日伟，程俊，等. 图像特征提取中领域尺寸和本征维数的自动选择算法[J]. 光电子·激光， 2013，24(12): 2416-2420.

Liu Fenglian, Wang Riwei, Cheng Jun, et al. Auto-selected algorithm of the neighborhood size and intrinsic dimension for image feature extraction[J]. Journal fo Optoelectronics·Laser， 2013，24(12): 2416- 2420.(in Chinese)

[7] 黄璞，唐振民. 无参数局部保持投影及人脸识别[J]. 模式识别与人工智能， 2013，26(9): 865-871.

Huang Pu, Tang Zhenmin. Parameter-free locality preserving projections and face recognition[J]. Pattern Recognition and Artificial Intelligence， 2013，26(9): 865-871.(in Chinese)

[8] 李城梁，王仲生，姜洪开,等. 自适应Hessian LLE在机械故障特征提取中的应用[J]. 振动工程学报, 2013,26(5): 758-763.

Li Chengliang, Wang Zhongsheng, Jiang Hongkai, et al. Adaptive Hessian LLE in mechanical fault feature extraction[J]. Journal of Vibration Engineering，2013， 26(5): 758-763.(in Chinese)

[9] 骆志高，李旭东，赵俊丽，等. 利用马氏距离判别法准确实现对裂纹的识别[J]. 振动与冲击,2013,32(21): 186-188.

Luo Zhigao, Li Xudong, Zhao Junli, et al. Crack identification with mahalanobis distance discrimination method[J]. Journal of Vibration and Shock,2013,32(21): 186-188.(in Chinese)

[10]孙即祥. 现代模式识别[M]. 长沙：国防科技大学出版社，2002:136-140.

[11]李锋，王家序，杨荣松. 有监督不相关正交局部保持映射故障辨识[J]. 仪器仪表学报, 2013,34(5): 1113-1116.

Li Feng, Wang Jiaxu, Yang Rongsong. Fault identification method on supervised uncorrelated orthogonal locality preserving projection[J]. Chinese Journal of Scientific Instrument,2013,34(5): 1113-1116.(in Chinese)

[12]宋涛，汤宝平，李锋. 基于流形学习和K-最近邻分类器的旋转机械故障诊断方法[J]. 振动与冲击,2013,32(5): 149-153.

Song Tao, Tang Baoping, Li Feng. Fault diagnosis method for rotating machinery based on manifold learning and K-nearest neighbor classifier[J]. Journal of Vibration and Shock, 2013,32(5):149-153.(in Chinese)

[13] 刘忠宝，潘广贞，赵文娟. 流形判别分析[J]. 电子与信息学报,2013,35(9):2047-2050.

Liu Zhongbao, Pan Guangzhen, Zhao Wenjuan. Manifold-based discriminant analysis[J]. Journal of Electronics & Information Technology,2013,35(9): 2047-2050.(in Chinese)