基于多稳态随机共振的轴承微弱故障信号检测*

2017-01-09陆宝春张登峰

振动、测试与诊断 2016年6期

关键词：双稳态特征频率共振

冯毅，陆宝春，张登峰

(南京理工大学机械工程学院南京，210094)

基于多稳态随机共振的轴承微弱故障信号检测*

冯毅，陆宝春，张登峰

(南京理工大学机械工程学院南京，210094)

针对双稳态随机共振模型无法有效处理调制信号的缺点，提出了一种以包络信号为输入信号的自适应多稳态级联随机共振(adaptive multi-stable cascaded stochastic resonance，简称AMCSR)信号强化方法。首先，对振动信号进行包络解调，依据包络信号分布特点，选用与信号分布相匹配的多稳态随机共振模型；然后，以故障特征频率的频谱幅值为指标，采用蚁群算法自适应地优化随机共振模型参数；最后，以噪声为强化源和驱动信号，通过级联随机共振方法对包络信号中的故障特征频率进行逐级强化，获得故障特征成分的强化信号。对实测轴承振动信号的验证结果表明，该方法能够增强故障特征频率成分，有效地提取被其他频率成分淹没的微弱故障信号。

滚动轴承；包络信号；多稳态；随机共振

引言

随机共振(stochastic resonance，简称SR)是一种有效的微弱信号处理方法，它可以简单理解为：通过非线性系统作用，噪声能量向微弱信号转移，从而加强了原本微弱的信号。随机共振的产生必须满足3个要素,即具有势能垒的非线性系统、微弱输入信号以及噪声源，当三要素达到最佳匹配关系时，随机共振效应最强[1-2]。轴承出现早期故障时，由于故障信号过于微弱，传统方法对信号的处理结果并不理想，采用随机共振方法可有效强化微弱信号。文献[1]通过二次采样变换，将仅在小参数范围成立的经典随机共振理论扩展到大参数范围，为随机共振的工程应用提供了理论依据。文献[2]提出了级联随机共振方法，有效地提高了随机共振对微弱信号的增强效果。文献[3]采用蚁群算法优化双稳态随机共振参数，成功地提取了行星齿轮的故障信号。文献[4-7]采用双稳态随机共振方法，提高轴承信号的信噪比，再通过经验模态分解处理降噪后的信号，取得了一定效果。文献[8]采用倒频谱白化方法预处理输入信号，提高了双稳态模型对故障特征的强化效果。文献[9]将Woods-Saxon势函数引入随机共振，优化了双稳态随机共振模型。文献[10]提出了可增加噪声利用率的多稳态模型，其结构特点可处理非对称分布的包络信号。

以上研究表明，双稳态随机共振方法在机械故障诊断中具有显著的效果，但双稳态随机共振同时存在一定缺陷：a.故障轴承的振动信号具有调制特点，而故障信号特征频率成分主要存在于包络信号中，双稳态模型将满足正态分布的原始信号作为随机共振系统的输入，故障特征成分的强化效果并不明显；b.故障信号为复合信号，以信噪比为优化指标时，无法准确反映复合信号中某一特定故障特征频率的强化效果。针对问题a引入可处理非对称分布信号的多稳态模型[10]，以含有故障特征频率的包络信号作为输入信号，从而克服双稳态随机共振无法处理调制信号的问题；针对问题b，以故障特征频率的频谱幅值为优化指标，通过蚁群算法进行模型参数优化，可实现故障特征频率的选择性强化。

基于以上分析，提出一种以故障频率频谱幅值为自适应优化指标，以包络信号为输入的自适应多稳态级联随机共振方法，可解决双稳态随机共振的两种缺陷。试验对比验证了AMCSR方法的有效性。

1 双稳态模型及其缺陷

1.1 双稳态随机共振模型

双稳态模型[1-2,11]具有中间势垒和两个对称势阱，双稳态势函数表示为

(1)

对应的Langevin方程为

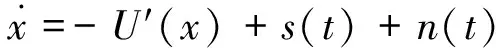
(2)

其中：s(t)为输入信号；n(t)为均值为0的高斯白噪声，其均方根为σ。

方程描述了布朗粒子同时受到输入信号和噪声驱动时，在双势阱中的过阻尼运动[1]。双稳态随机共振模型如图1所示。

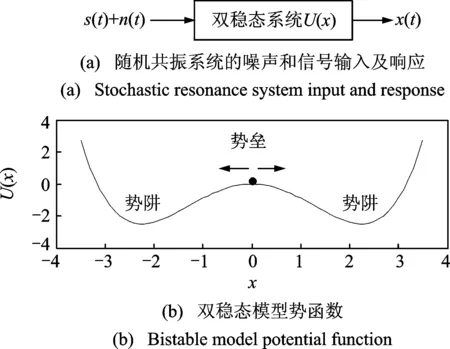
图1 双稳态随机共振模型Fig.1 Stochastic resonance model potential function

1.2 双稳态随机共振的缺陷

采用文献[11]中以信噪比为优化指标所获得的最优双稳态模型，通过输入不同类型的信号，验证双稳态模型随机共振的缺陷。

最优模型参数取值a=b=1，最优共振频率(在已知参数的随机共振系统中，唯一能得到最大程度强化的频率)信号s(t)=0.5cos(2π×0.1t)，即信号频率f=0.1 Hz，噪声均方根σ=5，采样频率fs=20 Hz，采样点数N=2 000。

不同类型输入信号的随机共振强化效果如下：

1) 在单一信号成分条件下，图2(a)中被噪声完全淹没的输入信号在经过随机共振系统处理后，输出信号的信噪比大为提高，频谱中0.1Hz频率的幅值非常显著，证明随机共振系统实现了噪声能量向目标信号能量的转换，从而加强了目标信号的能量，如图2(b)所示；

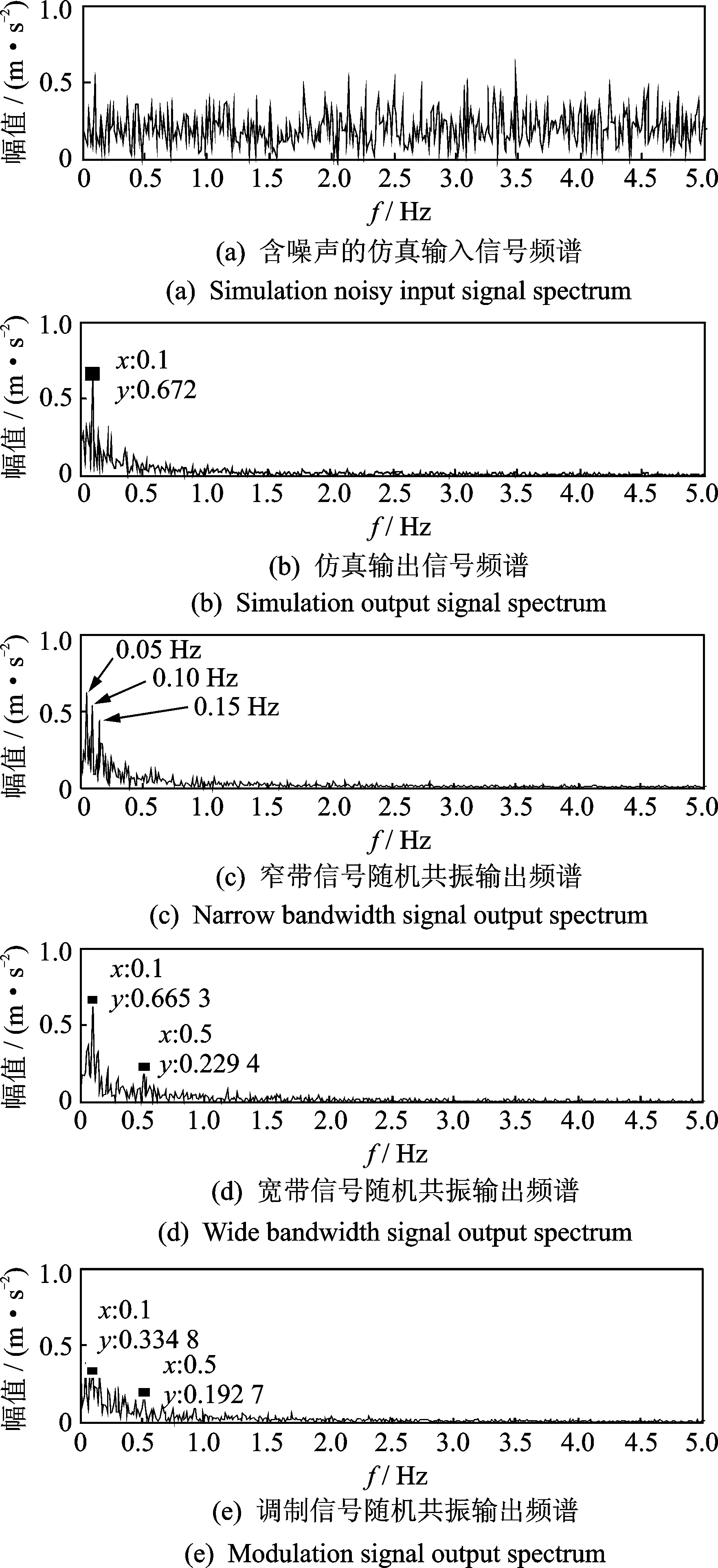
图2 复合信号随机共振Fig.2 Stochastic resonance of composite signal

2) 当输入信号为s(t)=0.5cos(2π×0.1t)+0.6sin(2π×0.15t)+0.4sin(2π×0.05t)，是以0.1 Hz为频率中心的复合叠加信号，随机共振仍能有效加强信号中的3种频率分量，如图2(c)所示；

3) 当输入信号为s(t)=0.5cos(2π×0.1t)+0.6sin(2π×0.5t)，信号成分0.5 Hz已远离0.1 Hz频带中心，0.1 Hz分量仍得到有效强化，如图2(d)所示；

4) 输入信号为s(t)=|0.5sin(2π×0.05t)|×cos(2π×0.5t)时，较高频率的0.5 Hz信号为主要成分，0.1 Hz调幅信号为包络信号，随机共振系统无法有效加强0.1 Hz频率成分，如图2(e)所示。

仿真结果表明双稳态随机共振存在以下缺陷：

1) 图2(c)与图2(b)结果对比表明，以信噪比为优化指标时，随机共振系统会强化最优共振频率附近的所有频率成分，无法针对性地强化0.1 Hz的最优共振频率；

2) 图2(e)与图2(d)结果对比表明，0.1Hz为包络信号时，双稳态随机共振系统无法有效强化具有调制特性的频率成分。

2 自适应多稳态级联随机共振

滚动轴承局部损伤对振动信号具有调制作用，而包络信号可有效地反映此类故障特征[12]。包络信号是非零均值的非对称信号，若用双稳态模型处理，在噪声影响下，上包络信号会越过中间势垒进入负半区势阱[1-2]，则会引入无意义的频率成分。

针对双稳态随机共振方法存在的两种缺陷，笔者提出了“自适应多稳态级联随机共振”方法，可对包络信号进行随机共振处理，实现故障特征频率的针对性强化。

2.1 多稳态随机共振模型

文献[10]提出了可增加噪声利用率的多稳态模型，其结构特点可以处理非对称信号。多稳态模型具有3个势阱和2个势垒的结构特点，如图3所示，其势函数可表示为

(3)

多稳态模型中的参数a，b均影响两侧势阱深度，且作用效果相反，参数c影响两势垒高度，通过调节系统参数a，c以及采样频率fs，获得最佳共振模型。

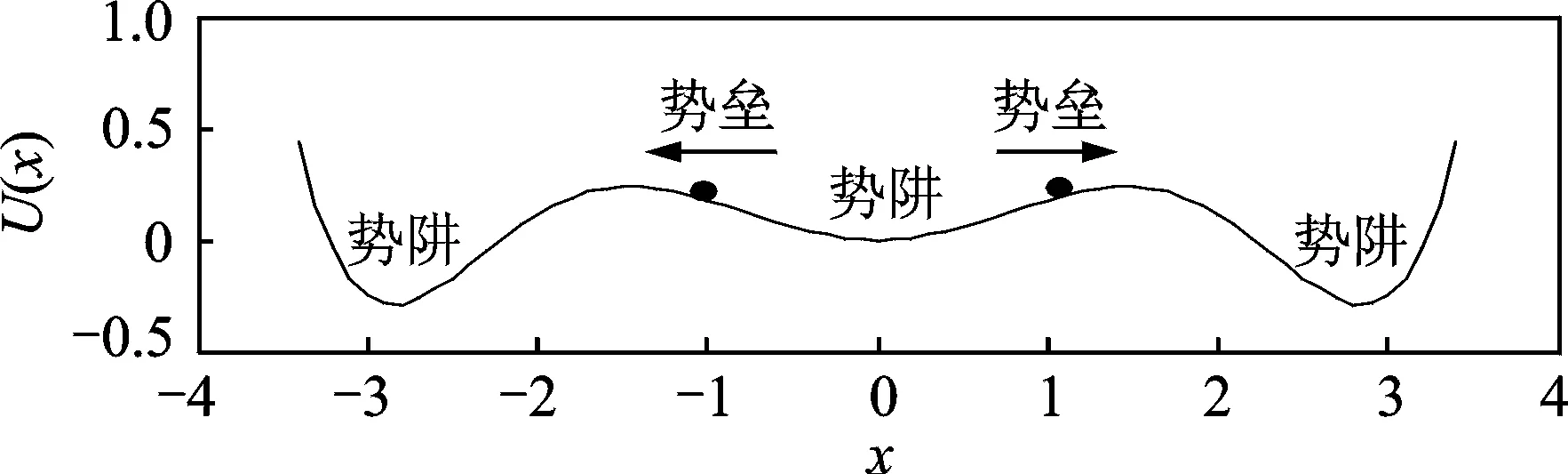
图3 多稳态模型势函数Fig.3 Multi-stable model potential function

2.2 包络信号多稳态随机共振

AMCSR方法具体处理步骤如下：

1) 采用Hilbert变换对振动信号进行解调，并提取轴承振动信号的上下包络信号；

2) 依据包络信号和包络谱幅值以及故障特征频率，按照大参数随机共振尺度变换方法[1]确定噪声强度以及初始共振参数范围；

3) 以待检测的故障特征频率频谱幅值为优化指标，采用蚁群算法进行参数优化得到最优共振参数；

4) 以噪声为驱动信号，对上下包络信号进行多稳态级联随机共振处理，获得强化信号。

其中，以噪声为驱动信号，即噪声信号在任意时刻t的瞬时幅值为正(负)，则以上(下)包络信号作为t时刻的系统输入信号，实现包络信号在多稳态模型中的随机共振。

(4)

其中：envu(t)为上包络信号;envd(t)为下包络信号。

级联随机共振[2]是以上一级随机共振的输出作为下一级随机共振输入的方式，将多个相同的随机共振模型串联，实现对微弱信号的逐级强化。多次仿真试验结果表明，采用两级随机共振级联，可以达到较理想的输出强化效果。包络信号多稳态随机共振算法流程如图4所示。

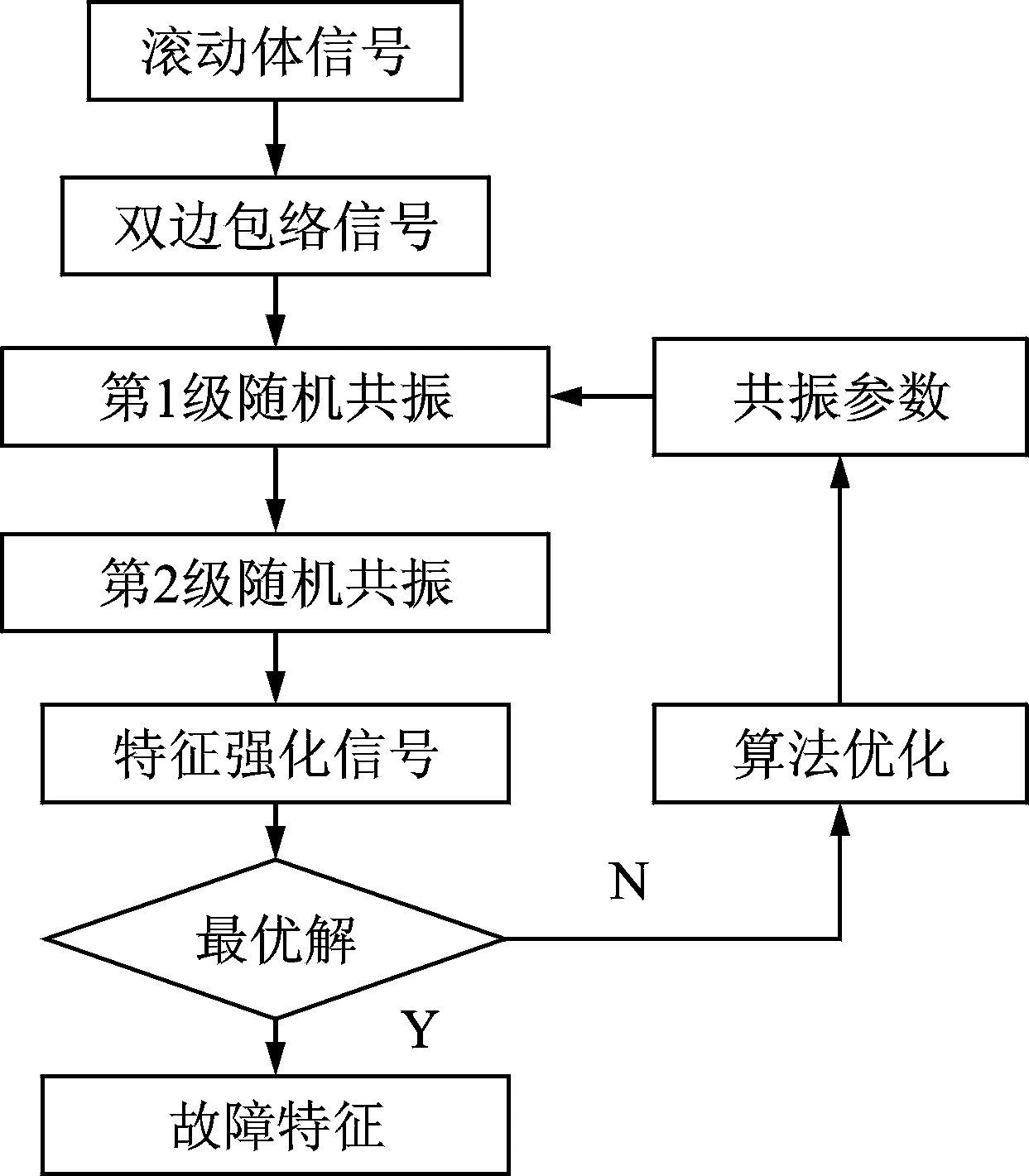
图4 算法流程Fig.4 Algorithm flow

2.3 自适应参数优化

多稳态随机共振系统对信号的处理效果受到多个参数的共同作用影响，若单一考虑某个参数则无法获得复杂系统的最优解。蚁群算法源于蚂蚁群体在觅食过程中，通过对路径上信息素浓度的更新，选择最优路径的现象，蚁群算法可有效解决多参数的寻优问题。

“小参数”(信号频率低于1Hz)随机共振并不适用于实际滚动轴承信号，因而需要对多稳态模型共振参数a,b,c,fs进行尺度变换，以适应“大参数”条件(信号频率远大于1Hz)的随机共振需求[1]。以文献[10]中的“小参数”条件下多稳态模型中的参数值为基础，采用文献[1]中的尺度变换方法得到“大参数”条件下的a,b,c值，并以此为各参数优化区间的中间值，通过多次试验，确定参数的优化区间(参数b固定不变)。同样，以实际采样频率作为fs的优化区间中间值，确定优化区间。

采用蚁群算法对共振模型参数进行自适应优化，获得最优参数。以滚动体故障为例，步骤如下：

1) 初始化ai→cj→fsk参数路径信息素，将所有路径的信息素置为相同初值τ；

2) 依据式(5)计算滚动体故障特征频率fball；

3) m只蚂蚁以随机ai为起点，按照参数路径，依据式(6)计算出的跳转概率进行下一步路径选择，直至m只蚂蚁均完成路径中的3种参数选择；

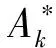
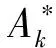
7) 依据更新后的路径信息素，重复步骤3～5，直至达到迭代次数上限K，获得全局最优参数。

上述步骤中，滚动体故障特征频率为

(5)

其中：ω为轴的转频；D为轴承节径；d为滚动体直径；α为接触角。

(6)

其中：n1,n2,n3分别为参数a,c,fs在寻优范围内的取值点数。

滚动体故障特征频率的频谱幅值大小A由离散傅里叶变换得到

(7)

其中：n为故障特征频率对应的频域离散值序号；x(kΔt)为信号采样值；Δt为采样间隔；k为时域离散值的序号N为序列点数。

信息素的挥发与增强表示为

(8)

其中：k为当前迭代次数；ρ为信息素挥发因子。

3 示例验证

3.1 自适应多稳态随机共振算法验证

算法验证采用的数据来自美国Case Western Reserve University轴承数据中心。轴承类型为6205-ZRSJMESKF深沟球轴承，信号采样频率为12 kHz，采样时间为1 s，驱动轴转速为1 797 r/min。轴承故障都预先人为加工，加工的故障部位分别为轴承内圈、外圈以及滚动体，深度尺寸均为0．177 8 mm。通过经验公式计算得到外圈、内圈和滚动体故障特征频率分别为107.3，162.2和141.5 Hz(实测频率存在误差)。

外圈和内圈故障的包络谱图5(a)，(b)中含有明显的故障特征频率，可判断内圈、外圈存在故障。由于滚动轴承结构特点，滚动体在运行中存在公转、自转以及打滑，工作状态相比外圈和内圈更为复杂，滚动体的特征信号非常微弱，往往被其他频率成分淹没，致使滚动体故障难以确定。

图5(c)中难以观察到明显的故障特征，且与内圈、外圈故障特征具有明显区别，可判断该轴承不存在内圈、外圈故障，但可能存在滚动体故障。依据经验公式，对待测信号中的滚动体特征频率进行随机共振增强检测。

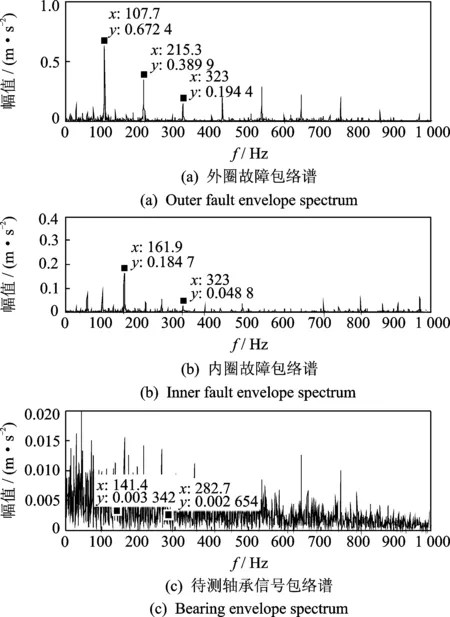
图5 轴承信号包络谱Fig.5 Bearing signal envelope spectrum

对待测轴承信号进行Hilbert变换得到上、下包络信号，如图6(a)所示。依据包络信号幅值波动范围，取噪声参数σ=3.5。由于白噪声频谱为均匀分布，含噪声的包络信号频谱中，所有频率成分得到一定增强，但故障特征频率仍不明显，如图6(b)所示。

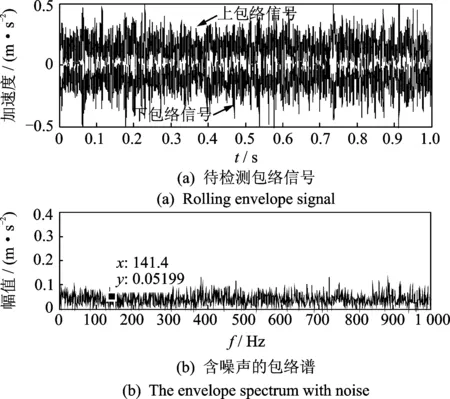
图6 待测包络信号和含噪声包络谱Fig.6 Rolling envelope signal and spectrum

依据大参数随机共振尺度变换方法[1]，设置参数b=1 000固定不变，其余参数的优化区间为a∈[500,2 000],c∈[50,800],fs∈[4 000,16 000]，取值步长分别为sa=2,sc=1,sf=5。

依据多次试验输出所得故障特征频率幅值的平均值，为保证在算法趋于收敛时信息素更新的增强幅度逐渐减缓，设置蚂蚁数m=100，全局路径信息素初值τ=0.2，信息素挥发因子ρ=0.05，设置迭代次数为K=2 000。

算法收敛时得到全局最优参数，将最优二次采样频率fs固定，分析参数a,c对幅值A的影响。参数a,c同时改变时，输出结果会出现局部极值，若单一考虑某一参数则无法获得最优结果。寻优结果表明，在参数a∈[1 300,1 400],c∈[400,500]区域内存在全局最优解，蚁群算法对多参数优化具有良好效果，如图7所示。

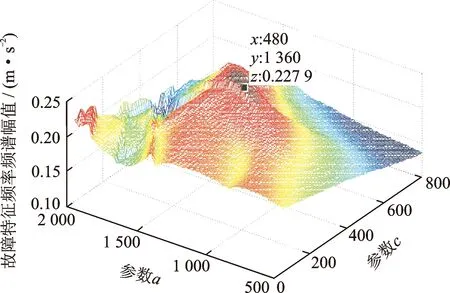
图7 蚁群算法寻优结果Fig.7 Ant colony optimization algorithm results

经过蚁群算法优化后的随机共振参数为a=1 364,c=483,fs=7 835。将最优参数赋值于随机共振系统，采用最优模型以及最优二次采样频率对输入信号进行处理，再按原有采样频率12 kHz绘制输出信号频谱。

依据最优共振模型参数，对含有噪声信号的上、下包络信号进行两级多稳态随机共振处理。由图8多稳态级联随机共振输出可知，第2级随机共振输出信号主要集中在以加速度幅值0，+2,-2 m/s2为中心的邻域范围内，对应多稳态模型的三势阱结构，呈现出明显的多稳态特征。

故障特征频率的频谱幅值从随机共振增强之前的0.051 99经过第1级随机共振增强至0.179 6，如图8(a)所示。同时，频谱中故障特征频率的边频带成分也受到一定程度增强，但故障特征频率的增强不够显著。经过第2级随机共振，故障特征频率的频谱幅值大幅度加强至0.228，其频谱幅值明显高于边频带成分，如图8(b)所示。经过两级多稳态随机共振，输出信号中的噪声成分减少，噪声能量逐渐向故障特征频率信号转移。

对于滚动体故障特征频率的倍频282.8 Hz，采用同样方法获得相应的最优共振参数，并对其进行强化，输出结果如图9所示。

图9 倍频随机共振输出Fig.9 Fault multiplier stochastic resonance output

以上试验数据验证表明，AMCSR方法有效地增强了待测信号中的滚动体故障特征频率，与正常轴承相比，增强后的待测轴承信号中含有明显的滚动体故障特征频率成分，可判断待测轴承存在滚动体故障。

3.2 双稳态随机共振算法对比

文献[5]以未经过包络解调的待测轴承信号经过带通滤波处理后作为双稳态系统输入，以信噪比为优化指标进行共振模型参数优化。图10频谱中故障特征频率的幅值为0.000 121 6，与其他频率成分相差102量级，能量极其微弱，且远远小于图5(c)包络谱中故障特征频率的频谱幅值0.003 34。

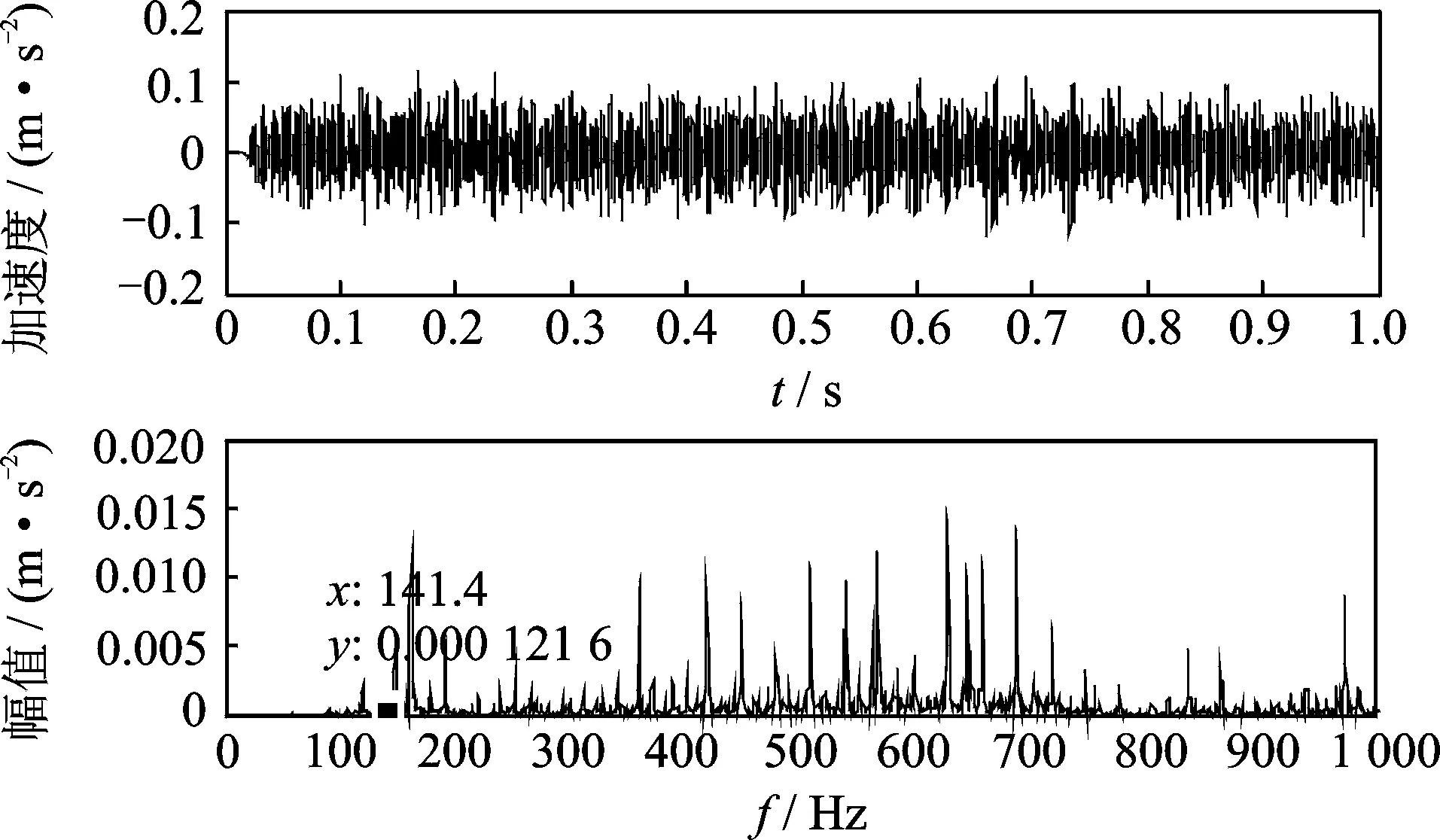
图10 带通滤波输入信号和频谱Fig.10 Band-pass filtering input signal and spectrum

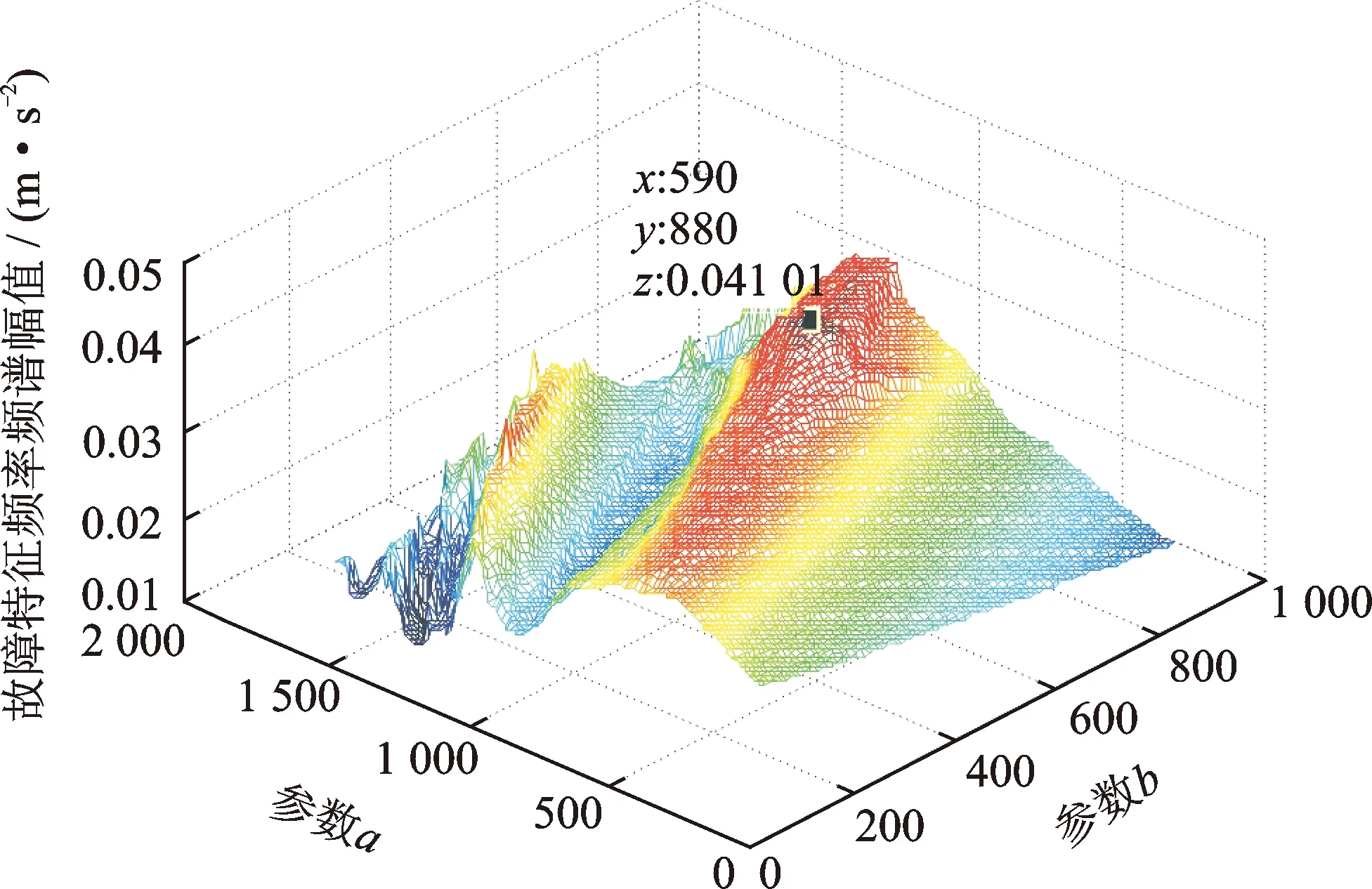
图11 参数与幅值关系Fig.11 Amplitude with parameters

将多稳态模型下的最优变尺度采样频率8 kHz作为双稳态模型寻优的二次采样频率，绘制参数a∈[10,1 500],b∈[10,1 000]与故障特征频率频谱幅值的关系谱，如图11所示。

由于输入信号未经过解调，导致强化后故障特征频率的频谱幅值仍然远低于其他频率成分。对于具有调制特性的故障轴承信号，双稳态随机共振的处理效果并不理想，如图12所示。

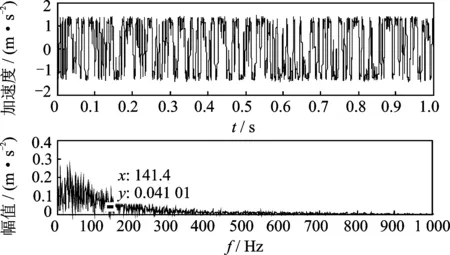
图12 双稳态模型随机共振输出和频谱Fig.12 Stochastic resonance output of bistable model

4 结论

1) 仿真信号分析与文献算法验证表明，以信噪比为优化指标的双稳态随机共振系统，会对共振频带中心内的频率成分无选择地加强，但对宽带信号和调制信号的加强效果并不理想。

2) 实例验证表明，上下包络信号多稳态级联随机共振方法对存在调制特性的故障轴承信号具有良好的强化效果。

3) 以故障特征频率频谱幅值为优化指标，自适应地优化多稳态模型参数，能针对性地增强轴承滚动体故障特征频率成分。

4) 随机共振方法存在一定不足，即需要已知故障特征频率的先验知识，因此随机共振适用于微弱信号的增强，而难以反映信号的细节特征。

[1] 冷永刚．双稳调参高频共振机理[J]．物理学报，2011，60(2)：1-7．

Leng Yonggang. Mechanism of high frequency resonance of parameter-adjusted bistable system[J]．Acta Physica Sinica, 2011,60(2): 1-7．(in Chinese)

[2] 冷永刚，王太勇，郭焱．级联双稳系统的随机共振特性[J]．物理学报，2005,54(3)：1118-1125．

Leng Yonggang, Wang Taiyong，Guo Yan. Stochastic resonance behaviors of bistable systems connected in series[J]．Acta Physica Sinica，2005, 54(3): 1118-1125．(in Chinese)

[3] Lei Yaguo, Han Dong, Lin Jing．Planetary gearbox fault diagnosis using an adaptive stochastic resonance method[J]．Mechanical Systems and Signal Processing, 2013, 38(1): 113-124．

[4] 张海如，王国富，张法全，等．改进的随机共振和EMD混合模型用于转子早期故障检测[J]．电机与控制学报，2014,18(2)：83-89．

Zhang Hairu，Wang Guofu，Zhang Faquan，et a1. Conjoint model combining improved stochastic resonance and empirical mode decomposition for rotor incipient faults detection[J]．Electric Machines and Control, 2014, 18(2): 83-89．(in Chinese)

[5] 韩东颖，丁雪娟，时培明．基于自适应变尺度频移带通随机共振降噪的EMD多频微弱信号检测[J]．机械工程学报，2013，49(8)：10-18．

Han Dongying，Ding Xuejuan，Shi Peiming. Multi-frequency weak signal detection based on emd after denoising by adaptive rescaling frequency-shifted band-pass stochastic resonance[J]．Journal of Mechanical Engineering, 2013, 49(8):10-18．(in Chinese)

[6] Li Jimeng, Chen Xuefeng, He Zhengjia. Adaptive stochastic resonance method for impact signal detection based on sliding window [J]. Mechanical Systems and Signal Processing, 2013, 36(2): 240-255．

[7] 雷亚国，韩冬，林京，等．自适应随机共振新方法及其在故障诊断中的应用[J]．机械工程学报，2012，48(7)：62-67．

Lei Yaguo， Han Dong， Lin Jing，et a1．New adaptive stochastic resonance method and its application to fault diagnosis[J]．Journal of Mechanical Engineering, 2012, 48(7): 62-67．(in Chinese)

[8] 张晓飞，胡茑庆，胡雷，等．基于倒谱预白化和随机共振的轴承故障增强检测[J]．机械工程学报，2012,48(23):83-89．

Zhang Xiaofei, Hu Niaoqing, Hu Lei, et a1．Enhanced detection of bearing faults based on signal cepstrum pre-whitening and stochastic resonance[J]．Journal of Mechanical Engineering，2012, 48(23): 83-89．(in Chinese)

[9] Lu Siliang, He Qingbo, Kong Fanrong. Stochastic resonance with woods-saxon potential for rolling element bearing fault diagnosis[J]．Mechanical Systems and Signal Processing, 2014, 45(2): 488-503．

[10]Li Jimeng , Chen Xuefeng , He Zhengjia. Multi-stable stochastic resonance and its application research on mechanical fault diagnosis[J]．Journal of Sound and Vibration，2013, 332(22): 5999-6015．

[11]胡茑庆．随机共振微弱特征信号检测理论与方法[M]．北京：国防工业出版社，2012:31-59．

[12]马川，李宏坤，赵利华．运用小波包峭度包络的滚动轴承故障诊断[J]．振动、测试与诊断，2011,31(6):720-723.Ma Chuan, Li Hongkun, Zhao Lihua. Rolling bearing fault diagnosis using wavelet packet-kurtosis-envelope[J]．Journal of Vibration, Measurement and Diagnosis,2011,31(6):720-723.(in Chinese)