多项式的问题特征对合并同类项迁移的影响

张令伟，连四清，王 晨



多项式的问题特征对合并同类项迁移的影响

张令伟1，连四清1，王 晨2

（1．首都师范大学数学科学学院，北京 100048；2．北京市第八中学，北京 100032）

多项式的合并同类项测试结果表明：正负号个数与字母个数对合并同类项的迁移成绩都有极其显著的影响，同类项间距离影响不显著；正负号个数与字母个数对合并同类项的交互效应极其显著．对能否完成合并同类项迁移的分析结果表明：正负号个数的变化与字母个数的多少对是否能在合并同类项中进行迁移有影响，而同类项间距离影响较小．

迁移；工作记忆；认知负荷

1 问题提出

通过比较源问题获得靶问题解决方法或途径，是学生学习数学知识和方法的基本心理机制，甚至被认为是解决新问题的唯一方法[1]．已有研究对源问题和靶问题的表面内容的相似程度（如，对源问题和靶问题有不同事件情节、不同事件类型和不同对象对应[2~4]的相似）对原理（源问题和靶问题在原理相同情况与原理不同情况[5]下的相似）的理解、领悟和运用做了较为深入的实验研究．然而大部分研究主要关注样例（即源问题与靶问题）的相似程度对迁移的影响，而且研究采用的测试材料主要是概率计算和代数应用题．采用的概率计算和代数应用题的表征形式多数是文字信息．

数学信息有文字、符号和图形3种表征形式，不同的数学问题在表征形式上具有较为明显的差异．如，多数情况下，概率计算、代数应用题为文字表征，文字信息在抽取数学关系时易受到无关信息的干扰，因而对其问题信息的认知具有较大认知负荷，从而影响源问题解决途径或方法的迁移．

自从提出样例设计要坚持减轻学生的工作记忆负担或认知负荷，研究者就逐渐开始关注单个样例设计中文字、符号、图形等多种信息源设计的合理性．在样例学习过程中，如果多重信息源的教学材料设计的不合理，将会分散学生的注意力从而增加认知负荷，产生“分散注意效应”，影响学生通过样例获得表征该领域知识的基本概念和图式[6]．其中，文本和图解的信息整合是一种视觉因素的整合，整合材料的视听表征可能提高问题解决的成绩和促进问题解决的迁移．Sweller[7]通过一系列实验说明了这一假设．结果发现：视听信息的整合促进了问题解决迁移的成绩[8]．通过Sweller的一系列实验表明图形和符号表征的信息对迁移有影响．

从已有的研究可以看出，在数学学科知识领域中，样例学习和呈现方式的研究涉及的知识主要是概率计算、相等关系理解和代数应用题．这些知识多以文字信息形式呈现，而对于多重信息源的数学知识对迁移的影响研究还比较少．数学学科领域的多重信息源呈现形式的知识对迁移影响与Sweller的实验结果是否一致，研究较少．代数中的多项式的知识呈现包含了文字、图形和符号等多种信息形式．为了研究多重信息源呈现形式的数学学科知识对迁移的影响，研究者以初中代数的多项式为实验材料，拟通过研究，探索多项式的问题特征对合并同类项的迁移的影响，从而为教师在多项式合并同类项教学中，选择样例呈现方式提供实验依据．

2 研究过程

选择北京市某中学的初一两个班的学生作为被试，两个班均为普通班，共61名学生．被试在实验前均没有学习过多项式合并同类项知识．

采用“4×2×2”三因素被试内设计．这里4表示负号个数，赋值为0、1、2、3；第一个2表示同类项间距离，赋值为0、1；第二个2表示字母个数，即每个单项式中含两个字母与含3个字母．负号个数、同类项间距离和字母个数均为被试内变量．研究变量为迁移成绩．

实验材料包括学习材料和测试材料．学习材料由3道合并同类项的例题和合并同类项法则组成．学习材料中的例题和法则由任课教师讲授．测试材料由16道测试题组成，按多项式中负号个数分别为0、1、2、3个，同类项间距离为距离等于0或1，字母个数为每个单项式中含2个字母与含3个字母编写测试题，每一类有一道测试题．在测试材料试卷上没有给出所学合并同类项的法则．为了消除题目的顺序影响，测试材料采用拉丁方设计，共16套测试问卷．

首先让任课教师讲解合并同类项例题和法则，被试在教师指导下学习十分钟学习材料，接着给被试发放测试材料，然后读指导语：“根据刚才学习的3道例题和法则，解答测试卷上的16道练习题，练习题完成的时间是15分钟．”15分钟后统一收回测试卷．

按满分6分的评分标准对被试答卷进行评分，答案完全不正确即不能迁移记0分；能找到同类项的记2分，能把同类项前面系数提出的记4分，能正确算出结果的记6分．

3 研究结果

对合并同类项问题解决迁移成绩进行描述性统计，结果如表1所示．从表1可以看出：与同类项间距离相比较而言，正负号个数和字母个数对合并同类项问题解决迁移成绩有一定的影响．对于字母个数为两个，在同类项间距为0与1情况下，正负号个数的4个水平的迁移成绩平均分从高到低依次是：水平1>水平3>水平2>水平4；对于字母个数为3个，在同类项间距为0与1的情况下，正负号个数的4个水平的迁移成绩平均分从高到低依次是：水平1>水平3>水平4>水平2．对合并同类项问题解决迁移成绩进行4×2×2重复测量方差分析，结果如表2所示．

表1 初中一年级合并同类项迁移成绩表

注：表中1、2、3、4分别表示正负号的水平1、水平2、水平3、水平4，也就是对应多项式中分别含有负号个数为0、1、2、3；1、2分别表示同类项间距为0、1；1、2分别表示多项式中每个单项式含有字母个数为2、3

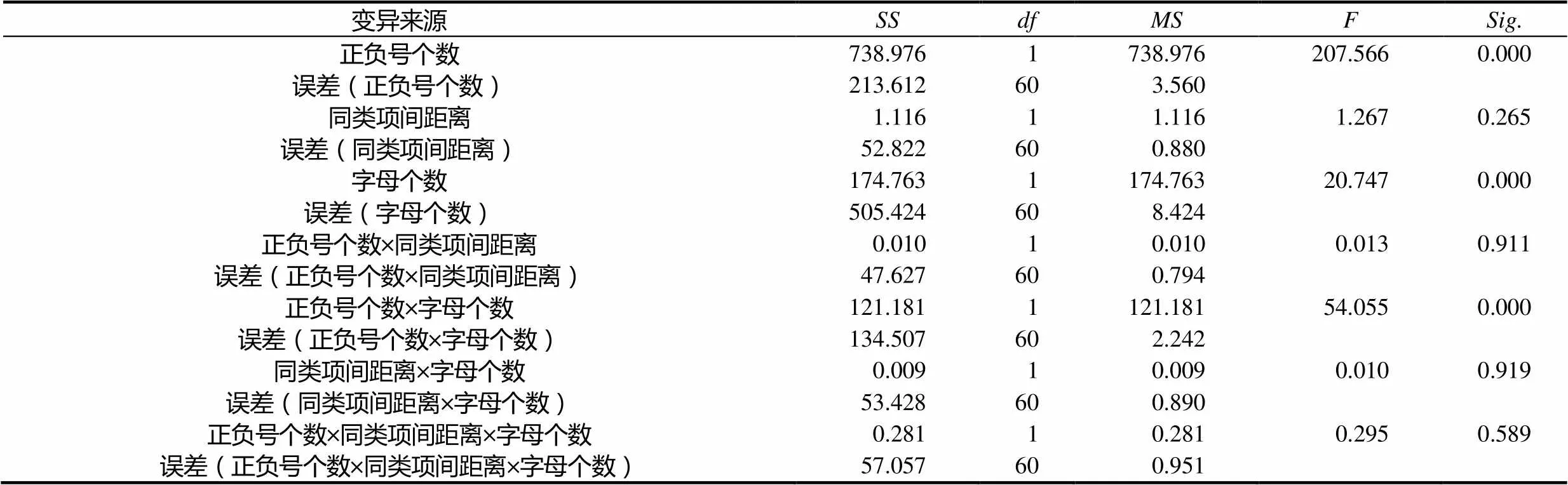
表2 初中一年级合并同类项迁移成绩方差统计表

表2数据表明：正负号个数的主效应极其显著（=207.566，=0.000），这说明正负号个数因素对迁移成绩影响极其显著；正负号个数的4个水平的迁移成绩平均分从高到低依次是：水平1（5.520 5）>水平3（4.582 0）>水平2（2.147 5）>水平4（2.114 8）；水平2与水平4对迁移成绩影响没有显著差异（=0.052，=0.821）．同类项间距离的主效应不显著（=1.267，=0.265>0.05），这说明同类项间距离因素对迁移成绩影响不显著．字母个数的主效应极其显著（=20.747，=0.000），这说明字母个数因素对迁移成绩影响极其显著．正负号个数×同类项间距离交互效应不显著（=0.013，=0.911>0.05），这说明正负号个数主效应不存在同类项间距离差异．正负号个数×字母个数交互效应极其显著（=54.055，=0.000），这说明正负号个数主效应存在字母个数差异．同类项间距离×字母个数交互效应不显著（=0.010，=0.919>0.05），这说明同类项间距离主效应不存在字母个数上的差异．正负号个数×同类项间距离×字母个数三因素交互作用不显著（=0.295，=0.589>0.05），这说明正负号个数×同类项间距离交互效应不存在字母个数差异．

进一步对正负号个数因素在字母个数的两个水平上做简单效应检验，结果显示：在字母个数为2水平上=301.014，=0.000<0.05；在字母个数为3水平上=38.718，=0.000<0.05．这说明对于字母个数为2与字母个数为3来说，正负号个数因素对合并同类项问题解决的迁移成绩都有极其显著的影响．字母个数为2与字母个数为3相比较而言，正负号个数因素对迁移成绩的影响不一致；在字母个数为2的水平上，正负号个数的4个水平的迁移成绩平均分从高到低依次是：水平1（5.697 0）>水平3（4.926 9）>水平2（1.2259）>水平4（0.819 7），在字母个数为3的水平上，正负号个数的4个水平的迁移成绩平均分从高到低依次是：水平1（5.344 3）>水平3（4.237 7）>水平4（3.409 8）>水平2（3.065 6）．正负号个数×字母个数交互作用如图1所示．

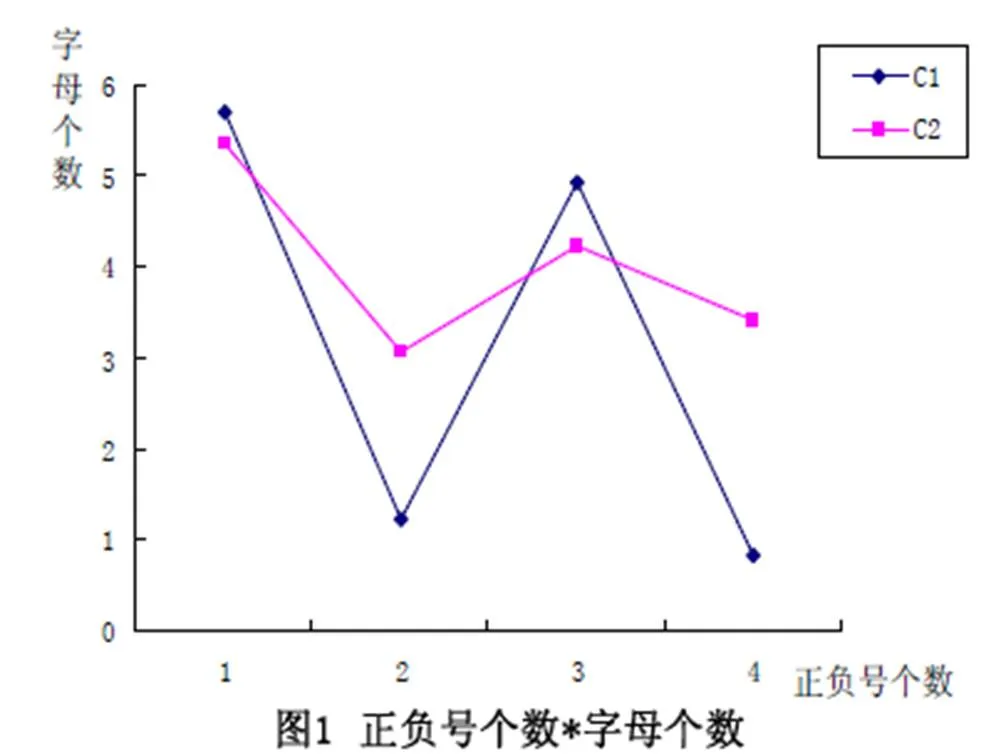
注：在图1中C1表示多项式中每个单项式含有字母个数为2，C2表示多项式中每个单项式含有字母个数为3

4 分析与讨论

实验的基本设想是：正负号个数对合并同类项迁移成绩有影响，正负号的个数不同对迁移成绩的影响不同；同类项间距离对合并同类项迁移成绩有影响，不同的同类项间距离对迁移成绩有不同影响；字母个数对合并同类项迁移成绩也有影响，且不同的字母个数对迁移成绩也会有不同的影响．

4.1 正负号个数对合并同类项迁移的影响

结果表明正负号个数的主效应极其显著，这说明正负号个数因素对合并同类项迁移成绩影响极其显著．这一结果与预期基本一致．结果说明，不同的正负号个数影响合并同类项的问题解决．其原因一方面可能是：学生先前的负数概念和正负数的加减运算法则不熟悉，导致合并同类项的步骤和结果错误，这是由于负数参与的运算（减法）要比正数的加法运算复杂的多，相对于减法运算来说，个体在计算加法运算时更倾向于使用提取策略[8]，而负数的负号具有符号和减法运算两个作用；另一方面可能是：在每个多项式中含有的4个单项式的系数正负情况中，除第一项系数均是正数外，其余三项系数的正负情况复杂（+++、++-、+-+、+--、-++、-+-、--+、---），在学生判断哪些单项式为同类项过程中，正负号个数干扰了这种判断．正负号个数的4个水平的迁移成绩平均分从高到低依次是：水平1>水平3>水平2>水平4；水平2与水平4对合并同类项的迁移成绩影响没有显著差异．这与长度效应理论基本一致，长度效应理论认为问题解决的信息越多，问题解决的长度越长，越容易引起错误[9]．在正负号个数的4个水平下的16道测题中，4个单项式系数分别为四正、三正一负、两正两负、一正三负，4个正数合并同类项没有给学生增加正负符号的认知负荷，因此4个正数合并同类项迁移成绩最好；相对于系数为4个正数而言，系数为两正两负的多项式增加了学生的工作记忆负荷，因此迁移成绩低于系数为4个正数的迁移成绩；而系数为三正一负和一正三负的问题长度几乎一样，都比系数为两正两负的问题的长度长，导致学生在判断哪些项是同类项以及合并同类项过程中，工作记忆负荷增加，因此迁移成绩最低．

4.2 同类项间距离对合并同类项迁移的影响

与预期有些不同的是，对于先前没有学习合并同类型的学生来说，同类项间距离的主效应不显著，也就是说同类项间距离因素对迁移成绩影响不显著．这说明同类项相邻或者有间距对判断哪些单项式是同类项以及合并同类项都没有显著影响．这与Sweller的注意分散效应和Mayer的空间临近效应不太一致．注意分散效应认为学习者在学习过程中必须参照多元表征的信息并加以整合才能理解，所以多元表征的信息最好在空间上临近，否则分散学生的注意而浪费整合信息需要的认知资源，从而无形中增加学生的外在负荷；空间临近效应是指意义相近的言语和图象在空间上临近呈现要比分离呈现效果好．与预期结果不一样的原因可能是：在测试题的3个变量中，相对于正负号个数和字母个数而言，同类项间的距离变量只有相邻和距离为1两种水平，变量水平的变化的判断需要的工作记忆负荷较少，产生的错误也相对较少．

4.3 字母个数对合并同类项迁移的影响

正如假设的那样，对于没有经验的被试来说，字母个数的主效应极其显著，也就是说字母个数因素对迁移成绩影响极其显著．这说明字母个数因素对判断哪些单项式是同类项以及合并同类项问题解决步骤和过程有影响．这与Sweller的实验结果基本一致．这是因为字母是一种代数符号，代数符号具有因素特性，它的储存和保持需要依赖语音环记忆；而且代数符号具有更多的视觉空间特性[10~12]，更多的依赖视空间记忆[13]．这就是说每个单项式都承载着视听信息，单项式中字母越多，单项式承载的信息量越大；在判断哪些项是同类项时，需要的视听认知资源也越多；而且代数符号的代数运算需要利用更多的工作记忆资源[14]．

[1] 曲衍立，张梅岭．类比迁移研究综述[J]．心理学动态，2000，（2）：50-55．

[2] 莫雷，唐雪峰．表面概貌对原理运用的影响的实验研究[J]．心理学报，2000，（4）：399-408．

[3] 莫雷，唐雪峰．事件类型的相似性对原理运用影响的实验研究[J]．心理科学，2001，（1）：5-8．

[4] Ross B H, Kennedy P T. Generalizing from the Use of Earlier Examples in Problem Solving[J]．, 1990, 16(1): 42-55.

[5] 莫雷，刘丽虹．样例表面内容对问题解决类比迁移过程的影响[J]．心理学报，1999，（3）：313-320．

[6] 邢强，莫雷，朱新明．样例学习的发展及问题[J]．心理科学进展，2003，（2）：165-170．

[7] Sweller J, Van Merrienboer, J G, Paas F G. Cognitive Architecture and Instructional Design [J]., 1998, (10): 25l-296.

[8] Campbell J, I D, Xue Q. Cognitive Arithmetic across Cultures [J]., 2001, (130): 299-315．

[9] Geary D, C Bow-Thomas, C C, et al. Development of Arithmetical Competencies in Chinese and American children: Influence of Age, Language, and Schooling [J]．, 1996, (67): 2 022-2 044.

[10] Reuhkala M. Mathematical Skills in Ninth-graders: Relationship with Visual-spatial Abilities and Working Memory [J]., 2001, 21(4): 387-399.

[11] Anderson, J R，Qin Y, et al. An Information-processing Model of the BOLD Response in Symbol Manipulation Tasks [J]., 2003, (1): 241-261.

[12] Kirshner D. Visual Salience of Algebraic Transformations[J]., 2004, 35(4): 224-257.

[13] 孙雨静，连四清，张洪山．语音环路和视空间模板在同底数幂比较过程中的作用[J]．数学教育学报，2007，16（2）：55-58．

[14] Anderson J R, Reder L M, Lebiere C. Working Memory: Activation limitations on Retrieval [J]., 1996, 30(3): 221-256.

Effect of the Problem Characteristics of Polynomial on the Transfer of Combining Similar Items

ZHANG Ling-wei1, LIAN Si-qing1,WANG Chen2

(1. Mathematics Science Institute of Capital Normal University, Beijing 100037, China;2. Beijing No.8 High School, Beijing 100032, China)

Experimental results show that: the main effect of the number of positive and negative is extremely significant; the main effect of the number of letters is extremely significant; the main effect of the distance of similar items is not significant. In addition, the interaction between the number of positive and negative sign x number of letters is extremely significant.

transfer; working memory; cognitive load

[责任编校：陈隽]

G420

A

1004–9894（2016）03–0093–03

2016–01–06

张令伟（1976—），女，河北邢台人，博士生，中学一级教师，主要从事数学教育与心理测量研究．