福建省小学教育专业数学预备教师本体性知识调查研究

甘火花，王 贞



福建省小学教育专业数学预备教师本体性知识调查研究

甘火花1，王 贞1，2

（1．闽南师范大学教育科学学院，福建漳州 363000；2．福建省莆田市城厢区霞林学校，福建莆田 351100）

采用问卷调查，从小学数学教材涉及的数与代数、图形与几何、统计与概率、综合与实践4个领域出发，考察了福建省内高校小学教育本科专业有意从事小学数学教学工作的大四学生本体性知识状况及可能的影响因素．调查结果表明：该省小教本科大四学生数学预备教师的本体性知识在正确性和解释性两方面的表现均不乐观；高中的分科与大学的培养模式对师范生的本体性知识略有影响；教师招考、教育实习见习、数学教学法和数学专业课是师范生数学本体性知识的重要来源；小学数学教材的学习与分析有待加强；数学模块课程亟需改善．

小学教育专业；预备教师；本体性知识；数学；调查

1 问题提出

研究者们普遍有一种假设：教师要向学生传授相关领域的知识，首先需要自己具备足够的知识，教师不可能传授自己不知道的知识．教师具有的知识不是单一的，而是多种知识的融合，对教师知识结构的研究日益受到重视．教师知识结构的相关研究，国内较早给出的分类，侧重于知识的来源和功能，分为本体性知识、条件性知识和实践性知识[1]．这一分类比较简明，界定也较清楚，因此影响较大[2]．国外影响较大的当推舒尔曼，他把教师的知识结构分为学科知识、课程知识、一般教学法知识、学科教学知识、学习者及其特点的知识等7类[3]．如果把中外关于教师知识结构的分类进行比较，舒尔曼的学科知识大致相当于国内的本体性知识．“本体”是一个哲学概念，意即“事物的主体或根源”．数学教师的本体性知识是数学教师知识的主体和根源，包括“显性的可言传知识和隐性的默会知识，是数学知识、能力和素养的统一体”[4]．数学教师不但需要掌握一定程度的数学知识，还需要有能力把这些知识进行教育学的解释和心理学的加工，教师只有达到正确性、解释性和联系性3个维度水平才算真正掌握知识[5]．借鉴已有的相关研究，研究者认为小学数学教师的本体性知识是特定的小学数学知识、能力和素养的统一体，包括教师对小学数学概念、原理的正确理解以及对这些知识的教育学解释和联系．

高师院校是培养中小学教师的摇篮，2012年教育部《关于全面提高高等教育质量的若干意见》中要求高等院校创新人才培养模式，各师范院校也在积极探索能适应21世纪经济社会发展、中国基础教育改革需要的中小学教师培养方略．目前在中国教师教育体系中，高师小学教育专业出现了多种培养模式，比较有代表性的有综合培养和分科培养．不同的培养模式已实施多年，在不同模式下培养出来的小学预备教师的数学本体性知识如何？能否胜任小学校的工作需求？哪些因素影响了他们小学数学本体性知识的掌握？已有的研究主要考察了职前教师对数学学科知识特定内容，如除法、面积、分数以及函数等方面的理解[6]，但鲜有对即将毕业的大四小教学生的数学本体性知识水平进行整体探究．研究基于小教专业大四师范生的数学本体性知识掌握程度会受到不同培养模式影响的研究假设，以福建省内高师院校小教专业有意从事小学数学教学工作的大四学生为研究对象，以小学数学学科中的基础知识为测试内容，考察福建省小教专业大四学生的数学本体性知识掌握情况，力图分析哪些因素影响了这些小学预备教师的数学本体性知识，为小学数学教师的职前培养提供某些启示．拟考察的问题有：

（1）福建省小教专业大四学生小学数学本体性知识掌握情况如何？

（2）不同培养模式下大四学生的小学数学本体性知识的掌握程度有否差异？

（3）哪些因素影响小教专业师范生小学数学本体性知识？

2 研究方法

2.1 被试的选取

通过高校网站查询，福建省开设小教本科专业的院校共8所，随机从6所高校中选取有意愿从事小学数学教学工作的大四师范生（以下简称数学预备教师）进行问卷调查和随机访谈，范围覆盖闽北、闽中、闽南、闽东等地区．问卷采用电子问卷和纸质问卷形式．纸质问卷发放50份，回收50份，电子问卷发放120份，回收54份．总计回收问卷104份，其中有效问卷78份，有效率75%，所得数据可作研究依据．

2.2 研究工具

2.2.1 本体性知识测试卷

研究以美国学者Ball的3方面检查法（正确性、解释性和联系性）[7]为依据编制本体性知识测试卷．但知识的联系性较为复杂，体现在方方面面，需要进行专题研究，故此次问卷未对知识联系性进行专门考察，仅研究了小学数学预备教师本体性知识的正确性和解释性两个维度，分别对应测试卷的选择题、判断题、填空题和简答题．

基于已有研究者[5~6，8]对小学数学知识内容的研究文献，参考《全日制义务教育数学课程标准（2011年版）》，研究的测试范围涵盖数与代数、图形与几何、统计与概率、综合与实践4领域，所占比例41∶32∶21∶6，与教材比例相当．选取的内容有数和量的认识与计算，图形的认识与计算，位置与变换，统计与概率，数学广角知识，题目多根据学者的研究报告、讲座、小学数学课本和课标改编，分选择题、判断题、填空题和简答题，题型比例为15∶5∶5∶6．选择题、判断题、填空题主要考察预备教师数学本体性知识的正确性，只需呈现解题结果．但为了更深层次探测他们对该问题的深度理解，研究者还对参与调查的部分被试进行了随机访谈．简答题主要考察预备教师本体性知识的解释性，要求被试用数学语言进行描述和表达．在对测试工具进行预试的基础上，通过专家内容效度的评定分析和小学数学教师的实际测试，研究对测试工具的一些项目进行了修改和降低难度，形成正式测试卷．测试卷的Cronbach系数为0.677，该测量工具的可靠性较高．

考虑到测试卷的目的在于考察知识的正确性和解释性，在评价上采用了两种不同方式．正确性测试项目采用量化评价，该类型项目的答案有正误之分，答对题目就得到相应的分值，反之答错则得0分．解释性测试项目采用话语分析法．首先给出每一简答题的参考答案，并标注该项目答语中的关键词或者关键术语，然后通过对被试回答语言的关键词考核，以及语句之间的组织和表达，窥探预备教师对本体性知识的解释能力．

2.2.2 影响因素问卷

参考已有的相关研究[9~10]，研究从5个方面考察大四学生小学数学本体性知识的影响因素．具体包括：本体性知识来源，如：“您的数学知识主要来源于”；自我数学本体性知识水平评价，如：“您认为，您的数学知识相当于何种水平”；分科情况，如：“您在高中是文科生还是理科生”；对高校小教专业的课程设置建议，如：“您对高校数学方面的课程设置有何建议”；个人因素，如：“总的来说，您觉得数学学习是否有趣”，共15个项目．

2.2.3 数据处理

运用SPSS19.0软件对数据进行分析．本体性知识测试卷正确性题目采用总分、平均数和百分比进行描述；本体性知识测试卷解释性题目采用质性评价；预备教师所在院校培养模式、高中文理方向采用方差分析；影响因素题目多采用四级计分法，变量为等距变量，数据采用积差相关分析．

3 研究结果

3.1 数学本体性知识整体水平

调查结果表明，预备教师在小学数学本体性知识的正确性和解释性两方面的掌握情况均不理想．

3.1.1 数学本体性知识正确性整体水平

小教专业数学预备教师本体性知识成绩统计见表1．

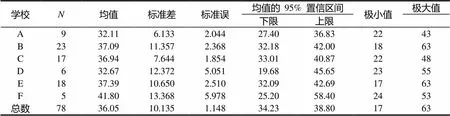
表1 福建省小教专业数学预备教师本体性知识成绩统计

从表1可以看出，预备教师在测验中的正确性题目整体平均成绩为36.05分（总分76分），最高分为63，最低分为17．按总分的60%取及格线为45.6，各校均未及格，成绩属中下水平．虽然D、F两校由于标准误较大不能较好地代表本校的水平，但从样本总数的情况看，标准差大而标准误小，所抽取的样本总数能反应福建省小教专业数学方向预备教师的整体情况．试卷的难度适中，除6道中档题和1道难题外，其余为小学毕业应掌握水平．可见福建省小教专业数学方向预备教师的本体性知识正确性掌握情况很不乐观．

通过对测试问卷的具体分析，发现预备教师在本体性知识正确性方面存在的问题多集中体现在对基础知识缺乏深入的思考和理解，掌握的知识停留在表面．如选择题中：为什么把0作为自然数？

A．因为0具有自然数的性质 B．因为0是测量的起点 C．为了使自然数能表示空集的基数 D．因为0是数轴的起点

有73.6%选择B、D选项，而选择正确选项C的只有26.3%．可见预备教师不了解由于集合论的创立引起自然数概念的发展．这一类似的题目，用“0度角和周角的区别”进行随机访谈，情况跟该题的结果差不多．有的说0度角是0度，周角是180度或它们的度数不同，也有的说始边和终边不同或大小不同，而从“旋转”或者“动态静态”的层面进行区别的很少．

在选择平均数还是中位数、众数来判断带有极值的数据时，有57.9%的被试选择了平均数，殊不知平均数易受极端值的影响．若数据中出现极值，应用中位数来判断．说明大多数被试不能有效区分平均数和中位数的使用条件．

再如：3、5、7、27、181、…这组数有规律．则下一个数是多少？

该题从国家教育部编制的《义务教育数学课程标准（2011年版）》中摘取并改编，难度为中等水平．面对一个中等水平题目，有33人选择弃填，整体正确率仅35.5%．测试后，对答错的部分被试进行随机访谈．之所以没有找到规律，是由于思维的定势和常规做法干扰了师范生思维的开放性和灵活性，可见师范生的数学思维能力也不容乐观．

对于小学数学教材中出现的数学概念及原理，预备教师多少能了解一些，但教材中没有明确给出解释或教学中不需要教给学生的知识，并不是所有预备教师都能知晓，暴露出来的问题是基本功不扎实，原理性知识功底不深厚．

3.1.2 数学本体性知识解释性整体水平

解释性指对数学事实、概念、规则、原理等进行解释的能力．测试卷的简答题为开放题，主要考察预备教师对数学本体性知识的解释水平．分析问卷后发现各高校小学数学预备教师的解释性能力也不强，存在着“知其然不知其所以然”现象．

如：“学习分数除法时，若有学生问您‘为什么除以一个数等于乘以这个数的倒数’该如何解释？”本题考察预备教师对运算法则算理的教育学解释．大多数被试多用演绎法进行论证，也有不少直接以“数学规定”来搪塞．当然也有举例子说明，并且回答较为完整，正确的．

又如，“在体操比赛中，评委给出的分数要去掉一个最高分，去掉一个最低分．请您解释这样做法的合理性．”多数测试者都能回答保证比赛的公正性，但这只是表面原因．为何能够更公正？为何平均数要去高低分才能更公正？这样的问题很少有人做出更深的解释．

简单的位移题目，被试者回答普遍存在描述不清、语义混杂或用词不准确等现象．在78份答卷中，能够准确描述清楚的仅有10份，大多数被试回答不够准确，如旋转没有写清中心或方向，平移没有写清距离或重合．

可见，预备教师对于数学本体性知识的解释大多停留在表面，即认为教材上写什么就是什么，很少主动对其原理进行思考．但在现实中，学生常常问“为什么”，教师若没有良好的数学知识积累，就难以解释这些“为什么”．

3.2 不同培养模式下小学数学预备教师本体性知识掌握情况

3.2.1 不同培养模式比较

在被调查的6所高校中，两所高校的小教专业为综合培养，其他4所为先综合后分科．由表2可知，分科培养的均值略优于综合培养，且抽取的样本能较好地代表总体的学业水平，这一结果也基本吻合了之前的研究假设．采用独立样本检验，比较分科与综合培养模式下不同高校本体性知识成绩的差异．方差满足齐性，预备教师数学本体性知识与大学培养模式之间不存在明显差异，即分科培养的预备教师的成绩虽高于综合培养，但总体差距不明显．

3.2.2 各领域比较

根据研究设计，测验主要从数与代数、图形与几何、统计与概率、综合与实践4个领域来考察小学数学预备教师本体性知识的掌握情况．结果发现，分科培养模式除图形与几何领域表现不如综合培养模式外，其它3领域的得分均优于综合培养．总的来讲，福建省小学数学预备教师在数与代数领域表现最好，图形与几何领域表现最差，这也印证了研究者在长期的教学中发现小教学生代数知识掌握较好但几何知识薄弱的直观感觉．

表2 不同培养模式下小学数学预备教师本体性知识成绩统计

3.3 本体性知识影响因素分析

3.3.1 数学本体性知识来源

对被试进行了自身数学知识的来源统计，要求被试选择自己的小学数学知识主要是通过何种渠道获得的．从统计的结果看，小学数学本体性知识的主要来源有大学前的数学课、教师招考、教育见习实习，数学教学法课、大学数学专业课．家教、微格教学、社团活动（如教师技能大赛）的影响较小．

3.3.2 数学水平

高珊指出，“教师入职时的学力对教师数学学科知识的正确性单独有显著影响．”[5]因此，在问卷中设计了大四小教毕业生的数学水平自评项目，要求被试从主观上评价自己的数学水平．统计结果见表3．

从表3可以看出，数学水平与测试成绩存在相关．在均值上，大学水平明显高于其它水平，高中、初中水平次之，小学水平的测试成绩最低．整体数据表明数学水平与测试成绩呈正比．但高中水平的标准差较大，说明高中水平的被试者内部水平不一，研究者猜想是否与高中的文理分科有一定关联．为验证猜想，采用独立样本检验比较高中文理科方向的差异．高中文理科者的测试均值和标准误理科略优于文科，但差距不大．

3.3.3 高中文理分科

由表4可知，高中文理科者的小学数学本体性知识有差距，理科优于文科，但优势不明显．为确保结论的可靠性，亦采用独立样本检验，验证高中不同分科与本体性知识成绩的相关性．方差满足齐性，小学数学预备教师本体性知识成绩与高中文理科方向不存在明显差异．

表3 福建省高校小学数学预备教师自评数学水平与本体性知识成绩统计

表4 福建省高校小学数学预备教师高中文理科生本体性知识成绩统计

接着比对了数学知识来源、高中分科和数学自评水平的统计分析，发现大学前的数学课是预备教师本体性知识的主要来源，高中文理科与本体性知识测试成绩相关但不显著，且数学水平自评与本体性知识测试得分呈正相关．进一步思考，在同一数学水平上，理科背景预备教师的小学数学本体性知识会不会比文科背景的好呢？在成绩统计的描述上，无论是高中和大学水平，理科背景的预备教师均高于文科，但从两个独立样本检验表格获知，高中水平的文理科和大学水平的文理科与本体性知识测试成绩并不存在明显相关，这与前面得出的结论一致．也就是说，无论是文科还是理科，只有达到高中水平就能胜任．所以总的来说，小学数学胜任能力要达到高中水平才较合格，而且水平越高越好，但数学水平与高中分科无明显相关．

3.3.4 课程设置建议分析

对于该维度的调查，采用开放问题形式．被试普遍觉得，当前的数学方向课程设置不够丰富，数学课程太少，对小学数学的研究不够，应大量增加可供选择的数学模块课程．同时，应降低大学数学课程学习的难度，多一些数学基础知识的学习，重视数学基础知识的加强；减少理论课程设置，增加与小学数学和教师招考的课程内容；增加技能课程，因为他们“经过实践发现，知道数学知识和讲授数学知识是完全不同的”．

3.3.5 个人因素分析

选取了学生得分与学习兴趣、学习能力、从业意向、对小学数学知识了解程度进行相关性分析．根据Pearson相关性分析，学习兴趣、从业意向与预备教师本体性知识得分无明显相关，但与数学水平和对小学教材的了解程度存在极其显著相关．另外，学习能力与数学水平之间存在极其显著相关，对小学数学教材了解程度又受到学习兴趣、能力、水平、从业意向等各方面影响．由此可以概括出，数学水平和对小学数学教材的了解程度直接影响小学数学本体性知识，学习兴趣、学习能力和从业意向对数学本体性知识产生间接影响．

4 研究结论及思考

4.1 研究结论

4.1.1 福建省高校小教专业数学预备教师的本体性知识整体水平不容乐观

本体性知识是教师具有的特定的专业知识，是教师进行教育教学的根基．从前面的分析可以发现，有意从事小学数学教学工作的小教专业大四师范生的本体性知识在正确性和解释性两个维度上的得分均不高，且各模块的成绩也不理想，表现在学生的基本功不扎实，知其然不知其所以然．在进行随机访谈的时候，一些被试大喊“它就是这样规定的，我哪知道为什么啊！”或者说“我老师就告诉我它是这样的，没告诉我为什么这样啊．”可见预备教师对一些数学知识还停留在“知道”水平，未能深入思考．另外，数学语言的表达和组织，小学生心理的换位训练，也是目前小教学生比较薄弱且需要强化的地方．

4.1.2 高中的分科与大学的培养模式对小学数学预备教师本体性知识略有影响

在本体性知识影响因素分析上，学校方面的因素分析基本印证了假设，但也有所出入．这里的假设是，在小教学生数学本体性知识方面，高中理科生优于文科生，大学分科培养优于综合培养．但调查结果显示，不同培养模式和高中分科，小学数学预备教师的成绩虽有差距但并不明显．无论是综合培养还是分科培养，无论高中是文科还是理科，均能满足成为一名小学数学教师的本体性知识需要．出现这样的结果有可能是测试题目设计的区分度不够明显．这里所设计的测试题目针对的是小学数学内容的掌握和理解，只要是学过小学数学就有能力作答，故对学习过小学、初中、高中知识的小教本科生来说，高中无论文理科都能作答．另外虽然各高校采取的培养模式各异，但在课程设置上却大体相似[11]，这在一定程度上也缩小了培养模式带来的差距．故在培养模式上综合与分科的预备教师在小学数学本体性知识的区别度并不高．

4.1.3 小学数学教材的学习与分析应加强

根据差异性和相关性分析，小学数学预备教师本体性知识的整体水平不高．他们的数学本体性知识与对小学数学知识的了解程度有低度相关，与数学水平之间存在极其显著相关．因此，预备教师不仅应具备比较宽广厚实的数学学科基础知识、基本原理，而且要研究义务教育数学新课标、新教材，熟知新课程理念、儿童心理学，构建层次清晰、内容完整、结构合理的小学数学知识体系．小教本科生由于缺乏对小学数学知识的了解和学情的把握，不知道考察的内容是几年级的，编写者有何意图，前后知识有何联系，因而导致对知识的解释大多采用近乎成人的演绎推理思维．

4.1.4 “教师招考”“教育实习见习”“数学教学法”和“数学专业课”是师范生数学本体性知识的重要来源．

教育实习见习、数学教学法和高等数学课是师范生获取数学本体性知识的重要来源，因此在课程设置的时候也往往是各高校的专业主干课．但从统计的数据看，无论是高中水平还是大学水平，都认为其数学知识主要来源于大学前的数学课．而在大学期间，高中水平者认为数学知识来源于实习、见习的占64.71%，是数学知识的第二大来源，仅有18.18%的大学水平者认为数学知识来源于实习、见习，却有72.73%的认为大学数学专业课是其数学知识的第二大来源．说明数学知识达到大学水平的预备教师，更加重视大学的数学课程，而高中水平者更加认可实习、见习等实践性的活动对自身数学知识的提高．

另外有平均超过一半的被试选择教师招考作为数学本体性知识的重要来源．可能的原因是教师招考目的性强，学生自主性得到充分体现，并且教师招考的内容与小学数学教学结合紧密．但教师招考一般在大四进行，且多是学生自发的学习，缺乏专业教师的常规指导．建议加强对学生的招考辅导和定期讲座，以解答学生在招考自学过程中产生的问题和疑惑．

4.1.5 小教专业数学模块课程亟需拓宽

通过调查发现，福建省小教学生对当前高校数学方面的课程设置不太满意，一是数学课程门类较少，二是技能实训课程不足，对小学数学的研究不够，建议应大量增加可供选择的数学模块课程．同时，应降低大学数学课程学习的难度，多一些数学基础知识的学习；减少理论课程设置，增加与小学数学和教师招考相关联的课程内容和实践环节；增加技能课程，如案例分析、教材解读、片断教学、说课，等等．

4.1.6 重视培养师范生的学习兴趣并强化从业意向．

兴趣和理想是行为的动力．从调查的结果看，虽然个人的数学水平和对小学数学的了解程度与数学本体性知识有显著正相关，但数学本体性知识间接受到学习兴趣、从业意向等因素的影响．因此，在小教专业的培养策略上，加强专业情感的培养、体验小学数学教师的价值，增强学习动力，强化从业意向，可以不同程度的提升小教学生学习数学本体性知识的兴趣．

4.2 对研究结论的思考

考虑到问卷涉及到的调查对象仅局限在福建省内的几所设有小学教育本科专业的高师院校，所以在做结论时持非常谨慎的态度．这些结论或许并不具有广泛的代表性，但有理由相信，研究还是具有某些启示作用的．

针对小教专业本科培养模式对小学数学本体性知识的掌握影响不大的结论，各高校是否应以2011年10月和2012年1月教育部相继出台的《教师教育课程标准》和《小学教师专业标准（试行）》为依据，研究具体的、可供操作的小学教育专业的本科规格和专业规格？

针对小教本科学生的数学水平应达到高中水平才算合格的结论，高师院校在招生时是否应严格把关，录取学生的条件除了高考成绩外，还应考察学生高中阶段在校的平时学业表现以及高中阶段的综合素质评价，做到宁缺毋滥？

针对小教师范生数学本体性知识解释性水平不高的现状，高师院校在进行教学时是否应有意识的训练学生数学语言的表达与组织？

针对小教师范生的小学数学教材的学习和分析应加强的现状，高校课程设置应如何做到小学数学知识的学习和大学数学知识的学习的平衡发展？

针对教师招考、教育实习见习对小教本科专业学生本体性知识获得的重要作用，高师院校应如何在实践中对学生进行针对性的指导和引领？

研究虽然取得了一些有意义的结果，但也存在着某些不足：首先，问卷的区分度把握不够，测查的深度和广度有待考证．其次，由于问卷调查的时间正逢大四学生备战福建省教师招考，使得调查对象的取证不够完整充足，样本容量较小，问卷回收率和有效率较低，研究结论可能不够准确．最后，在研究过程中，缺少更多研究方法的辅助．今后的研究应从扩大样本量、增加调查内容和采用多种研究方法入手，继续探讨小学数学预备教师本体性知识的掌握情况和影响因素．

致谢：在问卷调查过程中得到了徐瑞标老师、陈秀丽老师的帮助，在此表示诚挚感谢！

[1] 林崇德，申继亮，辛涛．教师素质的构成及其培养途径[J]．中国教育学刊，1996，（6）：16-22．

[2] 衷克定，申继亮．论教师知识结构及其对教师培养的意义[J]．中国教育学刊，1998，（3）：55-58．

[3] Shulman L S. Knowledge and Teaching: Foundations of the New Reform[J].，1987，（57）（1）：1-22．

[4] 曹培英．新课程背景下小雪数学教师本体性知识的缺失及其对策研究[J]．课程·教材·教法，2006，（6）：40-45．

[5] 高珊．北京市小学教师数学学科知识的调查与分析[D]．首都师范大学，2008．

[6] 李琼．小学数学教师的学科知识：专家与非专家教师的对比分析[J]．教育学报，2005，（6）：57-64．

[7] Ball D L. The Mathematical Understandings That Prospective Teachers Bring to Teacher Education [J]., 1990, (90): 449-466.

[8] 王智秋．构建高师小学教育本科专业数学类课程的若干思考[J]．课程·教材·教法，2002，（4）：69-72．

[9] 许昊，王刚，林武宾．大学生数学学习现状及其影响因素的探究[J]．教育研究，2007，（12B）：20-21．

[10] 朱家生，姚林．现代国际课程发展的趋势与我国数学课程改革的对策[J]．数学教育学报，2003，12（4）：10-13．

[11] 邓艳红．高等院校小学教育专业课程方案探析[J]．课程·教材·教法，2009，（2）：78-82．

Investigation of the Ontic Knowledge of the Preparatory Mathematics Teachers Majored in Primary Education in Fujian

GAN Huo-hua1, WANG Zhen1, 2

(1. Education Science Institute in Minnan Normal University, Fujian Zhangzhou 363000, China;2. Xialin School in Chengxiang District, Putian City, Fujian Province, Fujian Putian 351100, China)

This paper investigated the status of the ontic knowledge of the seniors who are eager to teach primary mathematics in Fujian and its contributory factors on the basis of the primary mathematic textbooks related to Number and Algebra, Graphics and Geometry, Statistics and Probability, Practice and Synthesis. The results showed: the correctness and the explanatory are not optimistic on the ontic knowledge of the preparatory mathematics teachers; the branch in senior schools and the training modes in universities have little influences on the ontic knowledge of the normal students; the teacher recruitment examination ,the education trainee and internship, the mathematics methodology and the specialized mathematics courses are important sources of the knowledge; the analytical abilities to the primary mathematics textbooks of the students need to be strengthened.

primary education major; preparatory teachers; ontic knowledge; mathematics; investigation

[责任编校：周学智]

G451

A

1004–9894（2016）03–0071–05

2016–01–26

2014年度福建省社会科学规划项目——福建省民办中小学青年教师专业发展研究（2014B187）；福建省教育科学“十二五”规划2014年度规划重点课题——高师院校青年教师教学能力的现状与提升办法研究（FJJKCGZ14-062）

甘火花（1974—），女，重庆奉节人，讲师，教育学硕士，主要从事教师教育与小学数学课程与教学研究．