云南民族地区六年级彝族学生数学问题解决表征水平的调查研究

孙雪梅，赵永香，朱维宗，潘永燕，张朝亮



云南民族地区六年级彝族学生数学问题解决表征水平的调查研究

孙雪梅1，赵永香2，朱维宗2，潘永燕1，张朝亮3

（1．曲靖师范学院数学与信息科学学院，云南曲靖 655011；2．云南师范大学数学学院，云南昆明 650500；3．云南省武定县民族中学，云南武定 651699）

以云南民族地区的几所城镇和农村小学的六年级彝族学生为研究对象，用6类小学数学问题解决为测试工具，通过纸笔测试法、口语报告法、作业分析法和比较研究法．发现六年级彝族学生在不同的数学问题解决中的表征水平有高有低，有的问题解决表征水平已达到了水平4，有的问题解决表征水平还处于水平1；六年级城乡彝族学生在有的数学问题解决中的表征水平有显著差异，在有的数学问题解决中的表征水平没有显著差异．另外，城镇彝族学生达到水平3和水平4的学生多于农村彝族学生，农村彝族学生处于水平1的学生明显多于城镇彝族学生；六年级彝族男生和女生的数学问题解决表征水平没有显著差异；六年级彝族数学优秀生和学困生的数学问题解决表征水平有显著差异；六年级彝族学生数学问题解决的表征水平与数学学习成绩显著相关，且为正相关．

彝族小学生；数学问题解决；表征水平

1 问题提出

彝族是中国西南地区历史悠久、人口较多、分布较广的少数民族．云南、四川、贵州和广西四省是中国彝族聚居区和彝族人口主要分布地，其中云南省彝族人口数为全国第一．云南的彝族主要分布在横断山脉南部、哀牢山脉、乌蒙山脉和金沙江、红河、南盘江流域．全省境内85％以上的县（市）都有彝族居住，其中尤以楚雄彝族自治州、红河哈尼族彝族自治州分布最多[1]．

1987年贵州师范大学在中国率先提出并开展了不同文化背景下数学教育研究．近20年来，民族数学教育日渐引起了社会各界的高度关注和重视．研究者对彝族数学教育进行了相关研究，主要有以下3方面：一是对彝族学生数学学习研究．李金富利用数学表征系统深入分析了四川凉山普格县彝族农村小学高段学生数学计算过程中思维差异，并对差异背后的文化、观念、习惯等影响因素进行了剖析．丁云洪等人对彝族农村小学4~6年级学生进行了数学问题解决观念的调查研究．二是对彝族数学教学研究．阿牛木支通过14年的教学研究和实践，探索了培养合格彝汉双语师资的培养途径和方法．三是对彝族数学及其数学文化的研究．吴双，周开瑞等对彝族数学及其应用进行了初步的归纳和整理．吉克曲一等人研究了凉山彝族文化中的数学文化．朱黎生研究了彝族服饰图案中的数学元素，并将这些资源应用于数学教学设计中．阿牛木支等探究了彝族毕摩从事宗教仪式中的插枝图中的数学思想和数学知识[2~7]．综上，教育界对有悠久历史和浓厚文化底蕴、人口较多的彝族的数学教育研究较少，而针对彝族义务教育阶段学生从表征视角探讨数学教与学的实证研究尚属空白．

“数学表征”是指用某种形式表达数学概念或关系的行为，也指形式本身．它既指过程，又指结果[8]．近年来，数学表征已成为人们研究数学学习心理的一种重要工具，它日渐受到数学教师的广泛认同和普遍重视．通过对学生在数学问题解决中的表征研究，能洞察问题解决者的思维过程，了解学生在数学问题解决中是如何理解所学的数学知识，是如何进行数学交流和数学思维的．为此，选取云南民族地区几所小学的六年级彝族学生为研究对象，通过调查研究他们在数学问题解决中的表征水平如何，以及表征水平是否存在群体差异性，并且表征水平与数学成绩间的相关性如何．旨在为了解少数民族学生数学学习的思维特征，改进民族地区少数民族学生的数学教学方式，为缩小民族地区数学教育差异，提高民族地区数学教学质量建言献策．

2 理论基础

数学问题解决是指运用已知的数学知识去探求和解决新的或不熟悉的情境中的非常规的数学问题的一种过程．数学问题解决既涉及数学陈述性知识（如数学概念、原理等），又涉及程序性知识（如运算、推理、作图等），还涉及认知策略（如表征、解题策略等），是一种高级的智力活动[9]．个体在解决数学问题时，先要在头脑中对题目的初始条件、约束条件、数量关系及问题等信息进行捕获、搜集、整合和加工，从而到达对题目的理解，然后再通过一系列算子，对知觉到的刺激或信息进行记录、表达并描述出来，这就是对数学问题的表征[10]．波文（Bowen，1990）指出，表征是问题解决者在问题解决时的状态结构，并且该结构是动态的，能反映问题解决者对任务的理解程度．他还认为表征可以形成一个系统，表征系统是问题解决者构造的能解决问题并能与他人交流的结构和过程的集合．表征不是问题解决过程的一个环节，而是持续整个问题解决过程中，数学问题解决的过程就是一个不断表征的过程[11]．

希尔伯特（J. Hilbert）等基于表征存在的形式以及表征在心理运作中的角色，认为数学表征应该区分为外在表征及内在表征．外在表征是指以语言、文字、符号、图片、具体物、活动或实际情境等形式存在的表征．内在表征是指存在于个体头脑里而无法直接观察的心理表征．而戈尔丁（G. A. Goldin）综合了数学教育领域对表征的研究，归纳了数学外在表征与数学内在表征的区别．他认为数学表征是反映数学学习对象（包括数学概念、命题和问题解决等；或数学陈述性知识、程序性知识、策略性知识和过程性知识等）的外在形式；数学内在表征则是指个体对数学学习对象的意义的赋予与建构，包括个体的语言语义、心象、视空间表征、策略及启发法、数学的情感体验等．数学外在表征的本质是数学学习对象的一个替代符号；数学内在表征是学习对象的外在表征内化在人脑中的心理表征，它本质上也是外在数学学习对象的一个替代符号．目前，对这两种表征的理解达成了如下共识：外在表征和内在表征是相互独立但又紧密联系的两个概念．由于对内在表征的研究在实际操作中有一定的困难，有的倾向于通过不同的外在表征类型间接地推测内在表征的过程，有的认为表征是一个内在表征和外在表征相互转换的动态认知过程[12~13]．

莱什（Lesh，1981）从交流的角度在布鲁纳的表征系统（动作表征、表象表征、符号表征）的基础上增加了口头语言和现实情境两种表征，把布鲁纳的动作表征称为操作模型表征，表象表征称作图像表征，符号表征称作书面符号表征．并构建了如图1所示的表征转化模型图．这几种表征方式同时存在于一个问题解决的情境中，当重新组织问题的构成要素和不同要素之间的联系时，个体要重复使用各种表征和表征序列；同一表征之间或不同表征之间是互动和相互转化的，内部的箭头代表同一表征之间的转化，联结不同表征的外部箭头表示不同表征之间的转化，不同的表征或转化呈现了不同表征水平．要实现表征之间的转化，学生就必须理解包含在给定的表征中的概念，而为了用其它表征方式来表征它，就必须重新解释这概念．学生正是在用不同的表征方式来表征数学概念并实现表征方式内部或者之间转化的过程中，获得了对数学概念的理解[12~14]．

根据以上理论和研究需要，文中通过对学生解答数学问题的外在表征方式来研究个体在数学问题解决中的表征水平．文中涉及的数学外在表征（以下简称“表征”）的形式分为以下3种类型：直观表征（包括现实情境、实物、具体操作、图表和图形表征）、语言表征（包括口语和文字表征）、符号表征（包括算术符号、抽象符号、代数式表征）．根据学生呈现的外在表征形式及其表现出来的所实现的表征间的相互转化情况，文中把表征水平分为以下几类：直观表征水平，是指问题解决者的推理是基于形象化的感知，即个体用直观的表征方式（如现实情境、图形、实物、具体操作等）来表征自己的思维过程和结果．程序表征水平，是指问题解决者通过程序，即用具体的算法、有序的步骤来表征自己的思维过程和结果，亦即实现了由直观表征、语言表征到算术符号表征的转化．抽象表征水平，是指问题解决者能够清晰地将概念与程序分离，能深刻理解概念的内涵，能抽象概括出数学对象的本质，即在更高水平上，实现了由直观表征、语言表征、算术表征到抽象符号或代数式表征的转化．

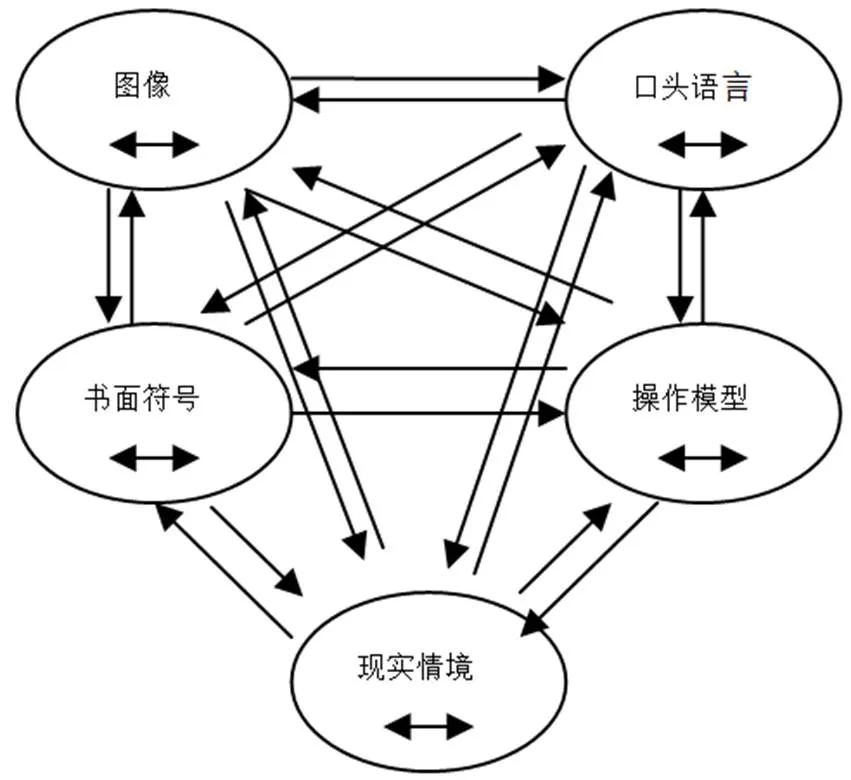
图1 表征转化模型

3 研究目的与方法

楚雄彝族自治州居住有彝、苗、傣、白、回、哈尼、傈僳等26个少数民族，少数民族人口占总人口的33%左右，彝族人口占全州总人口的26％左右．武定县位于楚雄彝族自治州东部，是一个集“山区、民族、宗教、贫困”四位一体的国家扶贫开发工作重点县．峨山彝族自治县是新中国诞生后的第一个彝族自治县，也是云南省的第一个民族区域自治县，全县居住着彝、汉、哈尼、回、蒙古族等，少数民族占全县总人口的63%左右．新平彝族傣族自治县的世居民族有彝族、傣族、汉族、哈尼族、拉祜族、回族、苗族、白族等，少数民族人口占全县总人口的71%左右，彝族傣族人口占全县总人口的64%左右．因此，选择楚雄彝族自治州武定县、玉溪峨山彝族自治县和新平彝族傣族自治县作为云南具有地域性、代表性的民族地区的几所城镇和农村小学的彝族学生进行调查，能客观地反映云南民族地区彝族小学生的数学问题解决状况和表征水平．

3.1 研究目的

通过调查研究，旨在了解六年级彝族学生数学问题解决表征总体水平如何，六年级城乡彝族学生的数学问题解决表征水平有否差异性，以及六年级彝族男生和女生、数学优秀生和学困生数学问题解决表征水平是否存在差异性，并对六年级彝族学生的表征水平与数学成绩间的相关性进行分析．从而得出客观真实的结论，为提高云南民族地区彝族小学生数学教学质量提供一定的理论参考和实践依据．

3.2 研究方法

3.2.1 被 试

城镇的学生选择了云南楚雄彝族自治州武定县和玉溪市峨山彝族自治县的城镇小学六年级彝族学生97人，农村学生选择了玉溪市新平彝族傣族自治县的农村小学六年级彝族学生79人作为直接样本．样本具体情况如表1所示．

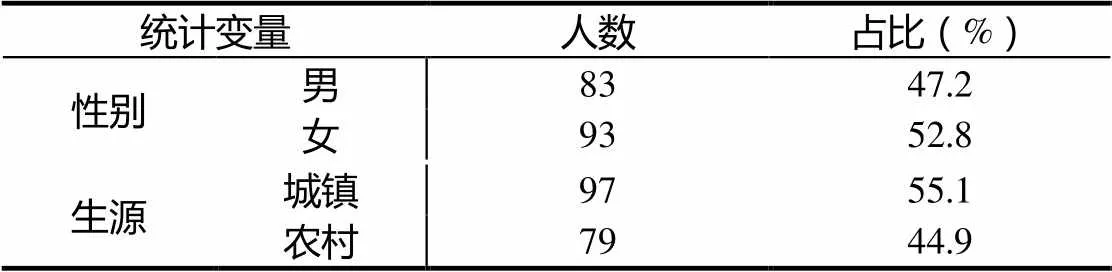
表1 样本情况

3.2.2 研究方法

纸笔测试法．用编制的《小学数学问题解决测试题》对学生进行测试，收集整理学生在数学问题解决中数学表征的相关信息并编码处理，利用SPSS17.0软件进行数据分析．

口语报告法．测试后，选择一部分学生，要求学生反思并回答其解题的思维过程．研究中，让学生对其所思、所想，毫无保留地报告出来，研究者通过录音笔录下来，再根据录音整理信息，然后通过对信息的分析提炼，以此揭示被试在完成任务过程中的思维和操作过程，以便能更准确地确定被试在数学问题解决中的数学表征类型及水平．

作业分析法．对学生解决数学问题的作业进行分析、比较．对他们解决问题的书面过程作分析，记录下学生呈现的数学表征的类型、表征水平，然后赋予相应分值，用SPSS17.0软件进行统计分析，最后进行归纳、分类，并得出结论．

比较研究法．对六年级彝族城乡、男女生、优秀生与学困生的数学问题解决表征水平进行比较．通过比较揭示各类彝族学生在数学问题解决中的表征特征和规律，从而得出客观真实的结论．

3.2.3 研究工具及信度

调查采用的是自编测试卷“小学数学问题解决测试卷”．测试试卷的题目主要参照QUASAR（Quantitative Under- standing: Amplifying Student Achievement and Reasoning）项目中的认知评价工具（Lane，1993；Lane等，1995）和蔡金法（2007）《中美学生数学学习的系列实证研究》中的测试题，结合学校和学生情况，设计了一份有10个题的测试卷，并请专家及一线教师对该测试题提出修改意见，删除了一些语意模糊、目的不清、针对性不强或难度大的问题．而后在一所小学进行了试测，并根据试测情况进行了再次修改，最后确定了6个题作为测试题（测试题详见附录）．

问题1是过程受限的数论问题，主要是考查学生的数感和运用数论基本知识解决实际问题的能力和建模意识．问题2是有关平均数的问题，主要考查学生对平均数概念的理解和方程意识．问题3是与模式有关的问题，主要考查学生的符号意识及推理和抽象概括能力．问题4是地图比例的问题，主要考查学生对比、比值及其应用能力．问题5是面积问题，主要考查学生运算和思维能力．问题6是过程开放的数论问题，主要是考查学生的数感、符号意识及推理能力[15]．这6个题都可用多种解题策略和多种表征方式来解答．

对回收的测试问卷做了信度估计，用SPSS17.0分析得到信度系数为0.788，所用问卷信度较好．由表2知，KMO检验系数=0.771，<0.005，说明所用问卷效度较好．

表2 KMO和Bartlett的检验

3.3 测试评价标准

评价标准关注学生在数学问题解决中涉及到的数学知识、策略知识和数学表征3个维度．按照对问题所涉及的数学概念和原理理解是否完全，使用的数学术语和符号的适当与否，算法是否完整且正确；是否会使用正式或非正式的相关的外在信息，是否明确问题的所有要素，是否理解它们之间的关系；问题解决的策略是否合适，解答过程是否完整且系统；给出的解答是否完整，使用的图表是否适当完整正确，使用的数学表达式和符号是否正确进行评价．具体的评价标准见表3[15]．

表3 数学问题解决评价标准

4 调查结果分析

为了从整体上掌握六年级彝族学生在数学问题解决中的表征现状，以便为后续的分析提供参考，数据处理时将学生解答6个数学问题所使用的表征类型及其水平进行了统计．文中用SPSS17.0统计软件中的频数分布分析法、卡方检验，以及Spearman等级相关分析法进行统计分析．

4.1 六年级彝族学生数学问题解决表征总体水平

六年级彝族学生数学问题解决表征总体水平如表4所示．

表4 六年级彝族学生数学问题解决表征总体水平百分率统计

统计数据表明：学生对数论问题解决的表征水平总体偏低：对于过程受限的数论问题，有50%的学生处于直观表征水平（即水平2），尤其是过程开放的数论问题，40.9%的学生无法进入该题的解答．但开放性数论问题中35.2%的学生处于程序表征水平（即水平3），22.2%的学生处于抽象表征水平（即水平4），均高于过程受限的数论问题．对于平均数问题，52.8%的学生处于程序表征水平（即水平3），这表明大多数学生对平均数的理解是工具性理解，只掌握了其算法；26.7%的学生处于抽象表征水平（即水平4），这部分学生对平均数的概念达到了抽象理解，形成了关于平均数的综合图式．有72.7%的学生在比例问题解决中处于程序表征水平（即水平3），表明这部分学生对比例的理解处于工具性理解，只有7.4%的学生达到了抽象理解水平．总体来看，在平均数、比例、面积3类问题解决中，大部分六年级彝族学生呈现的表征水平为程序表征水平（即水平3）；在模式问题解决中，有大部分学生达到了抽象表征水平（即水平4）；在解决过程受限的数论问题时，大部分学生的表征水平为直观表征水平（即水平2），而在解决过程开放的数论问题时，50%左右的学生的表征水平为程序表征水平（即水平3）或抽象表征水平（即水平4），但还有不少学生的表征水平还处于水平1．评价6个问题的各表征水平的具体描述见表5．

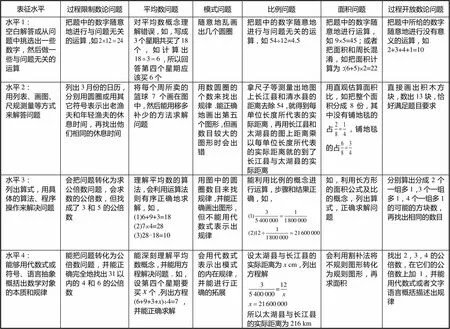
表5 六年平级彝族学生数学问题解决表征水平的评价描述

4.2 六年级彝族学生表征水平的比较研究

下面分别按城乡、性别、成绩分类对六年级彝族学生的数学问题解决表征水平进行差异比较．

4.2.1 六年级城乡彝族学生数学问题表征水平的比较研究

为了比较六年级城镇和农村彝族学生在数学问题解决中的表征水平是否存在差异，研究者对此进行了卡方检验．具体情况如表6所示．

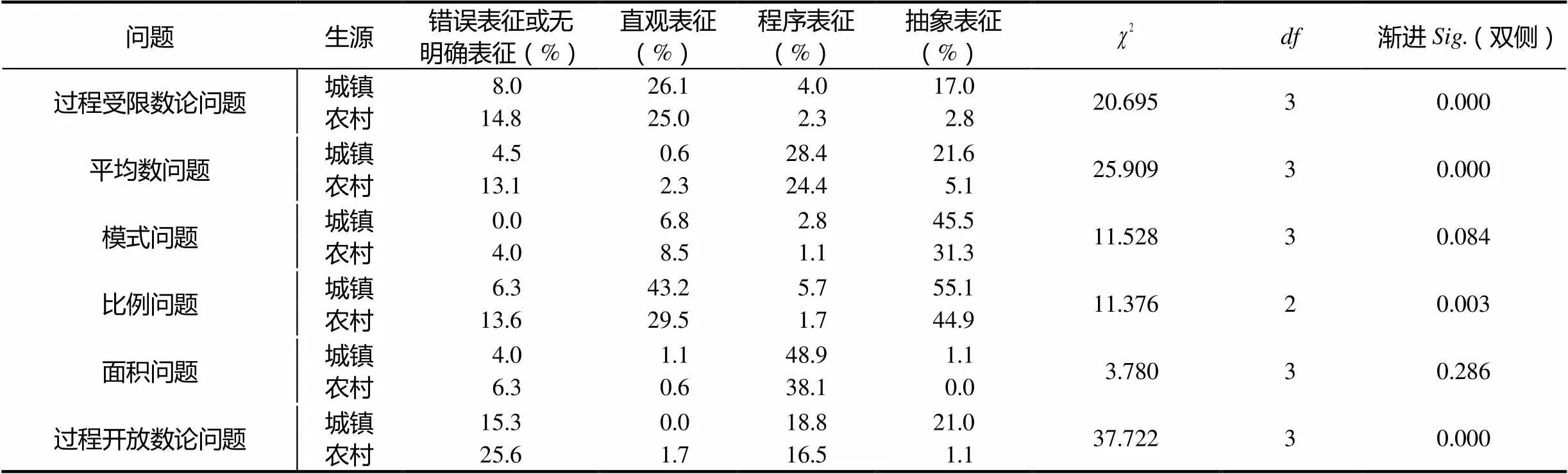
表6 六年级城乡彝族学生数学问题解决表征水平卡方检验

统计数据表明：六年级城乡彝族学生在数论、平均数、地图比例3类数学问题解决中的表征水平有显著差异（<0.05），在模式、面积两类数学问题解决中的表征水平没有显著差异（>0.05）．另外，城镇学生程序表征水平和抽象水平的学生多于农村彝族学生，错误表征或无法进入数学问题解决的农村学生明显多于城镇彝族学生．

4.2.2 六年级彝族男女生表征水平的比较研究

为比较六年级彝族男生和女生在数学问题解决中表征水平是否存在差异，对男生和女生数学问题解决表征水平进行了卡方检验，具体情况如表7．

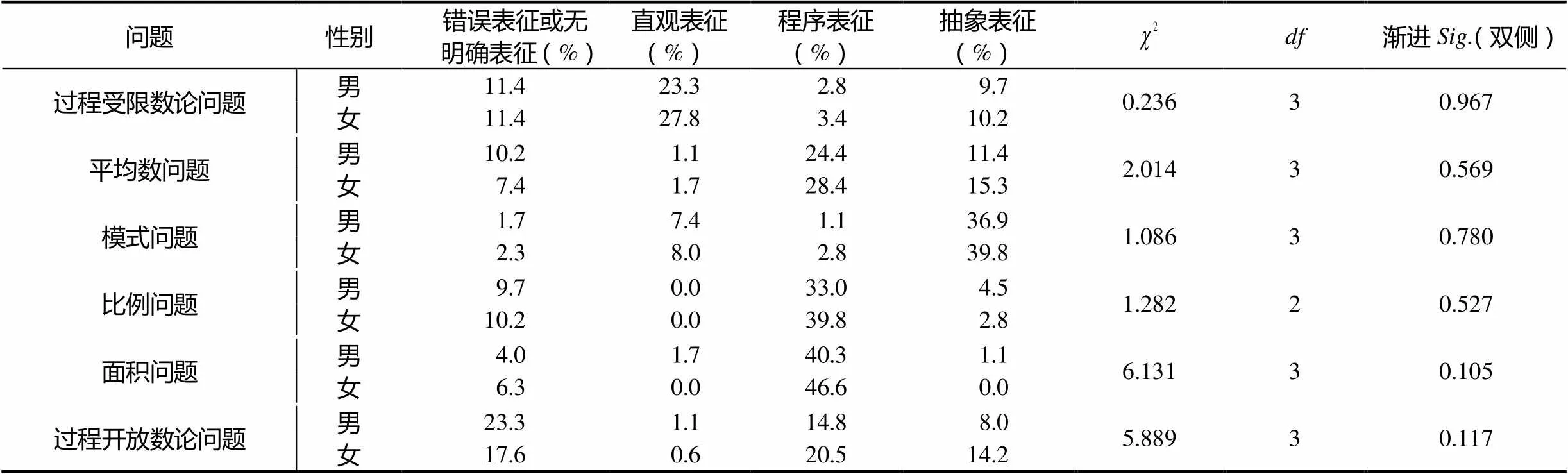
表7 六年级彝族男女生数学问题解决表征水平卡方检验

统计数据表明：对于所测试的6道题，值均大于0.05，说明六年级彝族男生和女生数学问题解决表征水平没有显著差异．

4.2.3 六年级彝族数学优秀生与学困生表征水平的比较研究

为比较六年级彝族数学优秀生和学困生数学问题解决表征水平之间的异同，对优秀生和学困生的数学问题解决表征水平进行了卡方检验，具体情况如表8．

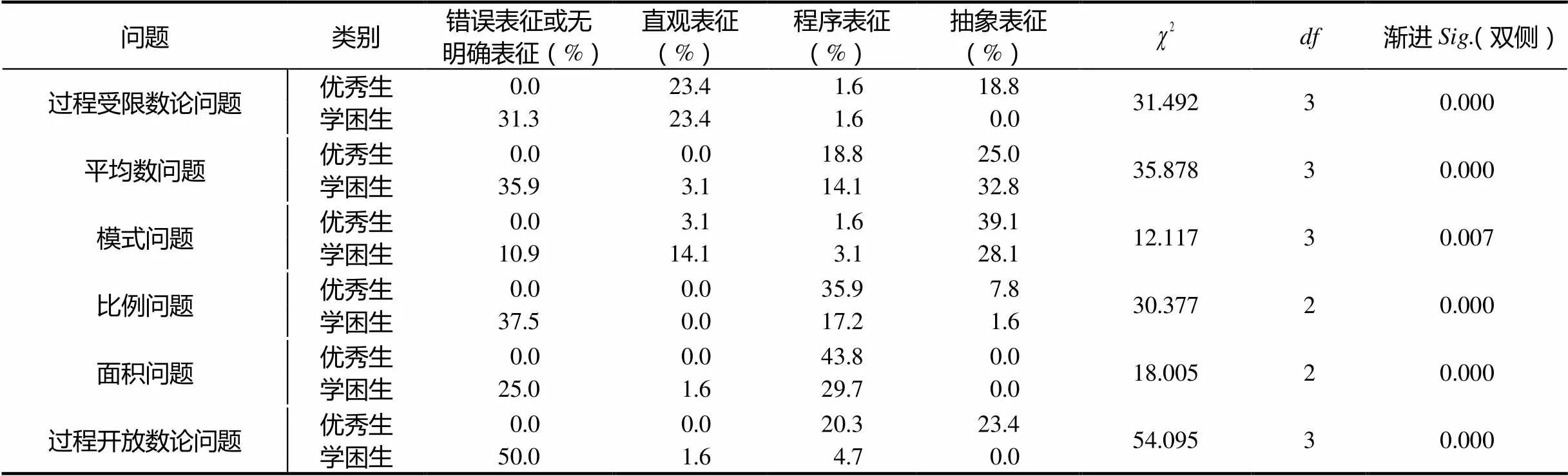
表8 六年级彝族数学优秀生和学困生数学问题解决表征水平卡方检验

统计数据表明：6道题目的值均小于0.05，说明六年级彝族数学优秀生和学困生在这6类数学问题解决中的表征水平有显著差异．大部分彝族数学学困生没有能力进入这六类数学问题的解决，能够解答这6类数学问题的学困生数学问题解决表征水平基本处于直观表征水平（即水平2）或程序表征水平（即水平3），而大部分彝族数学优秀生对这6类数学问题解决的表征水平处于程序表征水平（即水平3）或抽象表征水平（即水平4）．

4.3 六年级彝族学生表征水平与数学问题解决成绩相关性

为了寻找六年级彝族学生数学问题解决表征水平与数学问题解决成绩之间是否有相关性，如果有相关性，相关性是否显著的问题．研究者对六年级彝族学生数学问题解决表征水平和数学问题解决成绩进行了Spearman等级相关分析，其中表征水平和成绩只能取有限的值，每个表征水平和成绩代表着不同程度，表征水平和成绩之间的差异无法衡量，符合Spearman等级相关分析的基本假设．具体情况如表9．

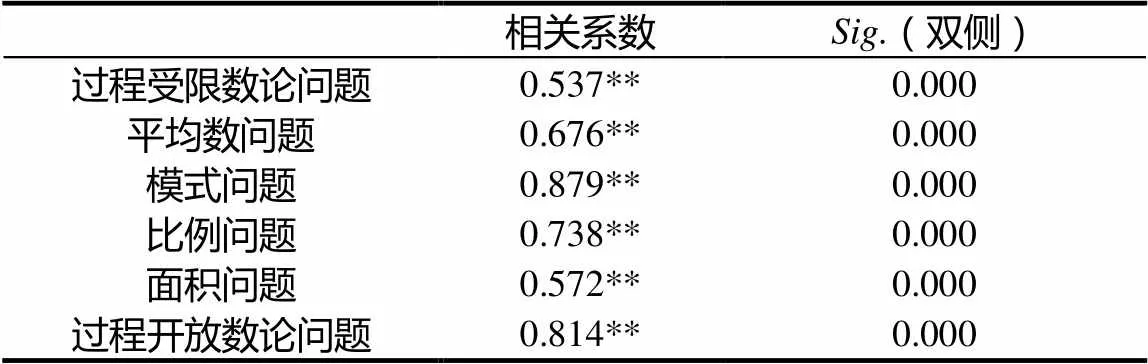
表9 表征水平与数学问题解决成绩间的相关性检验

注：**.在置信度（双侧）为0.01时，相关性是显著的

统计数据表明：对所测试的6道题的分析结果均显示<0.001，即六年级彝族学生数学问题解决表征水平与学习成绩显著相关，且为正相关．这说明学生的数学问题解决表征水平越高，学生在数学问题解决中的数学成绩越好．

5 结论和教学启示

5.1 研究结论

通过以上的调查研究可以得到以下结论．

（1）大部分六年级彝族学生在平均数、比例、面积数学问题解决中的表征水平达到了程序表征水平（即水平3），在模式问题解决中达到了抽象表征水平（即水平4），而在数论问题解决中的表征水平只达到直观表征水平（即水平2），甚至还有不少学生的表征水平还处于水平1．

（2）六年级城乡彝族学生在数论、平均数、地图比例3类数学问题解决中的表征水平有显著差异，在模式、面积两类数学问题解决中的表征水平没有显著差异．另外，城镇彝族学生达到程序表征水平和抽象水平的学生多于农村彝族学生，农村学生处于水平1的学生明显多于城镇彝族学生．

（3）六年级彝族男生和女生数学问题解决表征水平没有显著差异．

（4）六年级彝族数学优秀生和学困生在这6类数学问题解决中的表征水平有显著差异．大部分彝族数学学困生没有能力进入这6类数学问题的解决，能够解答这6类数学问题的学困生数学问题解决表征水平基本处于直观表征水平（即水平2）或程序表征水平（即水平3），而大部分彝族数学优秀生对这6类数学问题解决的表征水平处于程序表征水平（即水平3）或抽象表征水平（即水平4）．

（5）六年级彝族学生数学问题解决的表征水平与数学学习成绩显著相关，且为正相关．

通过测试可以看到在数学问题解决中的表征水平为程序表征水平的学生占的比例较大，说明大部分学生对能用具体的算法、程序操作来解决的问题完成得较好．学生遇到熟悉的问题，有现成的公式可利用时，如处理平均数、面积、比例等问题时学生就倾向于选择程序表征．其次，学生使用直观表征的频率是最少的．除了模式问题外，有一半的学生在过程限制的数论问题中使用了直观表征，在其它的4类问题中，学生极少使用直观表征．这与教材的编写注重抽象的解释和算法化的程序操作的特点，以及教师教学时喜好的表征倾向是有关的．同时也说明学生掌握了更高级的表征方式后，不再愿意使用繁复的、直观的表征方式．通过对测试卷的分析及学生的口语报告可以看到，能达到抽象表征水平的学生处理问题时，能较好地将现实问题转化为数学问题，并恰当地选择相应的数学知识和方法来解决问题，如遇到过程受限和开放的数论问题时，能将问题转化为公倍数问题来解决．并且这部分学生解决问题的方法多样，表征的方式也是多元的，且能较好地实现各种表征间的转化．这表明达到抽象表征水平的学生已从“算术思维”过渡到了“代数思维”，能顺利地找出问题中的等量关系并列出相应方程来解决问题，说明他们对方程的本质有了深刻的体会．测试表明，学生的数学问题解决表征水平越高，那么他们在数学问题解决中的数学成绩越好．这也说明直观表征最后必须上升到抽象表征才是“数学”，因为直观表征能帮助学生理解抽象的数学内容，并不能直接实现学生的深层次的数学理解，而数学优秀生和学困生的表征水平测试的结果也验证了此结论．处于水平1的学生，这部分学生大多是数学学困生，他们对问题涉及概念理解不清楚或理解错误，公式记忆不正确，算法错误，计算和推理能力欠缺，对问题的重要信息理解不清楚或理解错误，更谈不上能选择合适的策略和表征来解答问题[16~18]．

5.2 教学启示

根据以上研究所得结论，教师在教学中要给学生一定的时空，充分使用实物、模型、学具等，先让学生在动作操作、直观表征中思维，学会利用直观表征寻求解答，让学生从直观的角度来构建自己对数学概念、法则及关系的表征，以此帮助学生理解抽象的数学概念和思想方法．如果教师在教学中仅提供符号化、形式化的表征，基础差的学生因为难以理解数学内容的抽象意义，因而对数学学习望而生畏，甚至失去学习数学的信心．

教师在教学中要注意多元表征的使用，除了关注言语化表征（如话语文本、书写文本、数学公式、符号表示、逻辑表示等表征），还要重视视觉化表征（如图形、图象、图表、教学模型、动画、动作操作等表征）在数学学习中的促进作用．因为单一表征只反映数学对象的某个角度，完整理解数学对象需要从多个角度把握．多元表征能进一步丰富学生的知识结构，让学生能从多角度认识数学对象，从而增强学生对数学对象的深刻理解，提高学生学习数学的信心，最终促进学生从具体思维向抽象思维的发展．

教师在教学中要关注从“现实问题”到“数学问题”模型化的过程，以及从“数学问题的结果”到对“现实问题检验、解释、预测、解决及推广”的过程．教师和学生平时较多关注从“数学问题”到“数学结果”的过程，较少关注从“现实问题”到“数学问题”模型化思想的应用．学生在遇到如测试卷中的问题1（过程受限的数论问题）时，51%的学生选择用画出日历表，然后再按要求一个个数日期来找到正确答案．只有20%的学生会把这问题转化为“公倍数”的问题来解决它，有的虽然想到用公倍数问题来解决，但没有根据现实问题来检验结果的正确性，多找或少找了正确答案．在数学问题解决中，关注数学建模的过程，通过一题多解，或多题一解，能较好地促进学生对数学概念、法则和关系等数学对象的深入理解，提高学生提出问题、分析问题和解决问题的能力．

另外，通过与一些教育专家的交流，建议教师在教学中要从彝族的历史、文化、民俗、服饰、宗教、节日和生产生活中开发出适合彝族学生实际的数学教学资源，利用具有彝族特色的数学教学资源能让学生找到民族自豪感和认同感，从而激发学生数学学习兴趣．如果能用双语进行教学的老师要尽可能用彝汉双语进行数学教学，慢慢过渡到汉语教学，这样可以帮助彝族学生跨越语言障碍，更好地切合彝族学生思维特点，使学生能正确深刻地理解抽象的数学对象[19~22]．

6 反思与展望

研究以数学问题解决为载体试图了解云南少数民族地区彝族六年级学生表征状况，力求真实地反映学生在数学问题解决中的表征水平，从而以表征为视角分析研究民族地区民族数学教育的现状及存在的问题．但因为一些主观和客观原因，研究中还存在许多不足：问题的设计未能考虑到彝族学生的语言、习俗和生活环境等因素，导致学生对有些问题的理解不够清楚明确．另外，样本选择的代表性不够，只选取了部分民族地区，农村小学中的彝族学生的数量也不多．通过此次研究发现有许多值得进一步研究的问题，比如，彝族和汉族、其他少数民族学生数学表征问题的比较研究，各学段彝族学生数学表征问题研究，表征视角下民族数学教与学策略研究，彝族数学文化及教学资源开发等问题．唯愿此文能起抛砖引玉的作用，能引发教育工作者对彝族数学教育的深入研究．

[1] 《彝族简史》编写组．彝族简史[M]．北京：民族出版社，2009．

[2] 吕传汉，张洪林．民族数学文化与数学教育[J]．数学教育学报，1992，1（1）：101-102．

[3] 吴双，周群体，周开瑞．彝族数学初探[J]．西南民族学院学报（哲学社会科学版），1996，（17）：124-131．

[4] 周开瑞，周一勤，王世芳．彝乡数学杂谈[J]．西南民族学院学报（自然科学版），1994，（3）：331-340．

[5] 阿牛木支．彝族毕摩插枝仪式中数学知识的应用[J]．西昌学院学报（自然科学版），2005，（4）：75-77．

[6] 阿牛木支．彝族插枝图数学思想探讨[J]．西南民族学院学报（自然科学版），1999，（3）：330-332．

[7] 朱黎生．彝族服饰图案中数学元素的挖掘及其在教学设计中的应用尝试[J]．民族教育研究，2012，（3）：98-102．

[8] 巩子坤．程序性知识教与学研究[M]．南宁：广西教育出版社，2010．

[9] 张春莉．数学问题解决过程的内在心理机制[J]．华东师范大学学报（教育科学版），1998，（2）：55-63．

[10] 邢强，蔡兴华，单永明．外部表征和问题呈现方式对小学生数学应用题解决的影响[J]．数学教育学报，2014，23（4）：74-77．

[11] 李金富．彝族农村小学生数学思维差异研究——四川普格5~6年级计算测试调查[D]．西南大学，2012．

[12] 唐剑岚．国外关于数学学习中的多元外在表征的研究述评．数学教育学报，2008，17（1）：30-34．

[13] 唐剑岚．数学多元表征学习及教学[M]．南京：南京师范大学出版社，2009．

[14] 鲍建生，周超．数学学习的心理基础与过程[M]．上海：上海教育出版社，2009．

[15] 蔡金法．中美学生数学学习的系列实证研究——他山之石，何以攻玉[M]．北京：科学出版社，2007．

[16] 王光明，廖晶．“探索世界”范式及其对数学教育的启示[J]．课程·教材·教法，2013，（12）：116-119．

[17] 夏小刚，吕传汉．跨文化视野下中美学生数学思维差异的比较[J]．比较教育研究，2006，（8）：63-67．

[18] 张定强，蒋会兵，蔡娟娥．中国少数民族数学教育研究的回顾与展望——基于1993—2013年CNKI期刊数据的分析[J]．数学教育学报，2015，24（1）：69-74．

[19] 孙雪梅，赛麒麟，朱维宗．曲靖市农村中学高二理科生学习风格的调查研究[J]．数学教育学报，2012，21（6）：35-41．

[20] 任伟芳，偶伟国，龚辉，等．“工具性理解”“关系性理解”和“创新性理解”[J]．数学教育学报，2014，23（4）：69-73．

[21] 孙雪梅，潘永燕．基于表征理论的“鸡兔同笼”问题教学设计[J]．数学之友，2014，（24）：10-12．

[22] 李燕清，唐剑岚．京族和汉族小学生估算能力及影响因素的调查研究[J]．数学教育学报，2015，24（1）：60-63．

附录：小学数学问题解决测试卷

问题1（过程受限的数论问题）：海边有一个小渔村，村里有一老一少两个渔夫同住一个房子里．3月1日那天，他们开始打鱼，老渔夫连续打3 天然后休息1天（即3月1日、2日、3日打鱼，4日休息，5日、6日、7日打鱼，8日休息，以下依此类推……），年轻渔夫连续打5 天然后休息1天（即3月1日、2日、3日、4日、5日打鱼，6日休息，7日、8日、9日、10日、11日打鱼，12日休息，以下依此类推……）．有一位朋友想在3月份趁两人一起休息的日子去看望他们，这位朋友可以选哪些天去才能同时碰到他们俩？

用尽可能多的方式解决此问题，并写出你的全部解答过程．

问题2（平均数问题）：一商店出售篮球．下图列出了该商店在前三周售出的篮球数：

问此商店在第四周应该卖掉多少个篮球，才能使每周售出的篮球平均数为7？

用尽可能多的方式解决此问题，并写出你的全部解答过程．

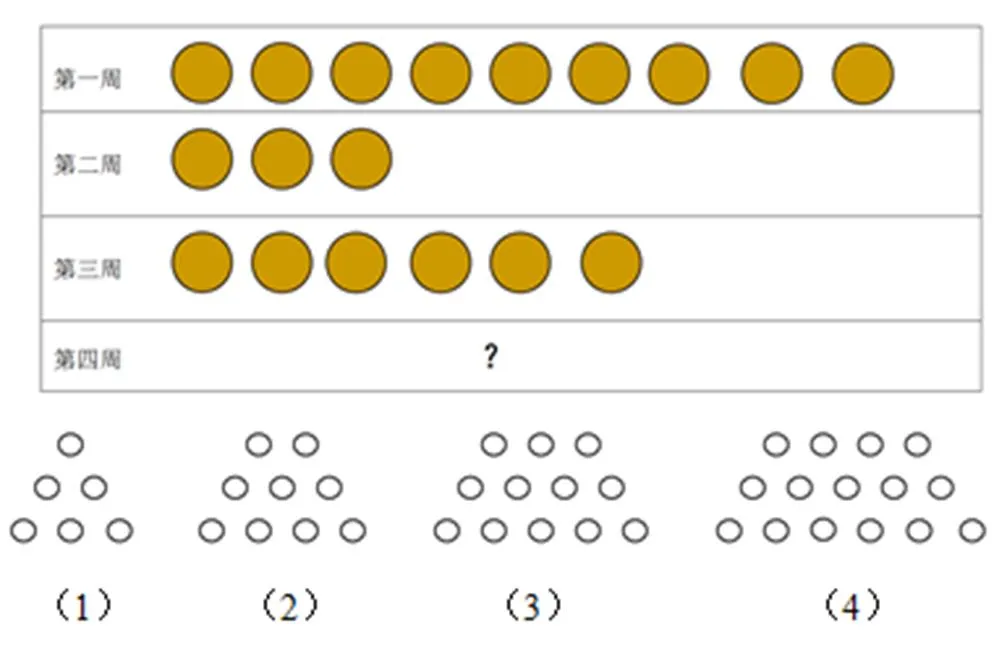
问题3（模式问题）：一些点按下面的模式排列．

（1）画出第五个图．

（2）画出第十个图．

（3）说明你为什么把第十个图画成这样．

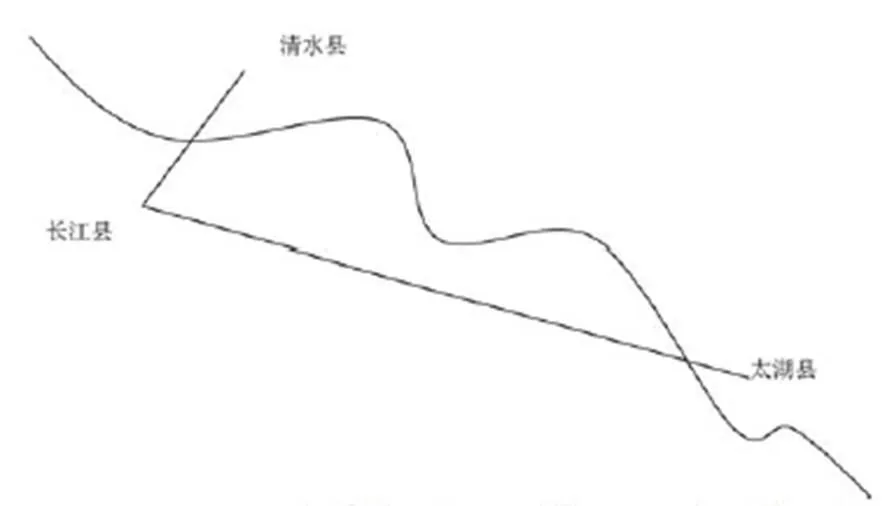
问题4（比例问题）：下面的地图上标有3个县城：

清水县与长江县的实际距离是54千米，在地图上，清水县与长江县的距离是3厘米，在地图上，太湖县与长江县的距离是12 厘米．太湖县与长江县的实际距离是多少千米？

用尽可能多的方式解决此问题，并写出你的全部解答过程．

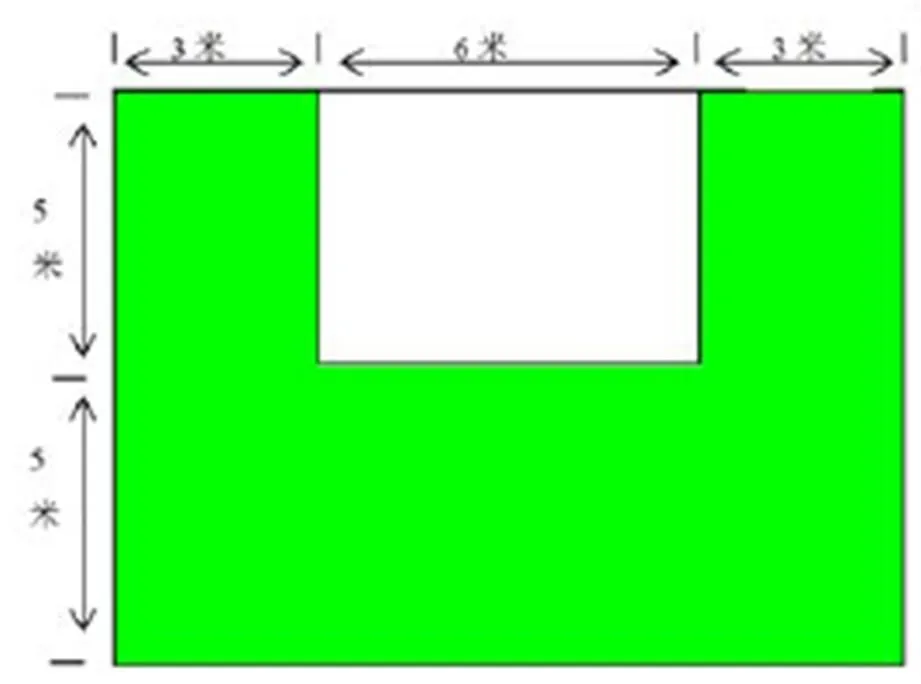
问题5（面积问题）：某小学有一间教室将变为校长办公室．

如上图，不铺地毯的地方将安置一张办公桌，别的地方会铺上地毯．

（1）没有地毯部分的面积是多少？写出你的解答过程．

（2）有地毯部分的面积是多少？写出你的解答过程．

（3）房间的几分之几铺了地毯？写出你的解答过程．

问题6（过程开放的数论问题）：李萍告诉她的弟弟李俊她在数学课上所做的游戏．

李萍说：“李俊，今天我在数学课堂上用了积木方块．当我把积木方块分成每2个一组时，多出了1个积木方块；当我把积木方块分成每3个一组时，还是多出1个积木方块；当我把积木方块分成每4个一组时，仍然多出1个积木方块．”

李萍问：“李俊，你猜猜总共有多少积木方块？”

李俊给出的答案是什么？

用尽可能多的方式解决此问题，并写出你的全部解答过程．

Study of Sixth-Grade Yi Students’ Capability of Mathematics Problem Solving in Yunnan Ethnic Region

SUN Xue-mei1, ZHAO Yong-xiang2, ZHU Wei-zong2, PAN Yong-yan1, ZHANG Chao-liang3

(1. College of Mathematics and Information Science, Qujing Normal University, Yunnan Qujing 655011, China;2. College of Mathematics, Yunnan Normal University, Yunnan Kunming 650500, China;3. Wuding Middle School of Yunnan Province for Nationalities, Yunnan Wuding 651699, China)

Selecting sixth-grade students of Yi nationality at town and rural in Yunnan ethnic region as research samples; using six categories of capability of mathematics problem solving as evaluation tools; completing pencil and paper test, verbal protocol, job analysis and comparative study, we found that sixth-grade students of Yi have different representation level in different capability of mathematics problem solving, some students reach representation level 4, some students only have representation level 1; there is a significant difference between some capability of mathematics problem solving and representation level, and there is NO significant difference between some capability of mathematics problem solving and representation level also. Furthermore, there are more students of town reach level 3 and 4 than students of rural; there are much more students of rural only have level 1 than students of town; there is NO significant difference between boys and girls; there is a significant difference between excellent students and students with learning difficulty; there is a significant correlation between representation level and math scores, and a positive correlation.

elementary school student of Yi nationality; capability of mathematics problem solving; representation level

[责任编校：周学智]

G420

A

1004–9894（2016）03–0085–08

2016–01–15

云南省教育科学“十二五”规划课题一般项目——云南民族地区5~6年级彝族学生在数学问题解决中的数学表征研究（BE14014）；曲靖师范学院2016年重点课题——云南少数民族数学文化的挖掘及其应用（2016JZ001）；曲靖师范学院2014年精品课程建设项目（JPKC2014003）；曲靖师范学院2015年研究生项目——5~6年级汉族和彝族学生在数学问题解决中的表征研究（2015YJS02）

孙雪梅（1970—），女，云南大关人，教授，硕士，硕士生导师，主要从事中小学数学教学研究及民族数学教育研究．