高中数学教师对问题串评价与编制的调查研究

高 翔，张 波



高中数学教师对问题串评价与编制的调查研究

高 翔，张 波

（扬州大学数学科学学院，江苏扬州 225002）

问卷调查表明：新手型教师与经验型教师对涉及概念命题的探究课问题串设计评价差异不显著，而对解题或者试卷讲评课的评价差异显著，暴露出新手型教师对于解题、数学知识本身的理解与经验型教师存在差距；经验型教师在编制问题串的过程中比新手型教师更加注重激发学生的学习兴趣、驱动学生“回归课本”以及将知识点进行“串联”；教师对问题串的评价能力与其编制问题串的能力相互影响．

新手型教师；经验型教师；问题串；评价

1 问题提出

教育家陶行知先生曾经说过“发明千千万，起点是一问；智者问得巧，愚者问得笨”．可见问题在教学中的地位之重．教师为了推进教学或者指导学生学习，会根据主题，提出一系列的问题，并约定俗成地把这一系列的问题叫做问题串．教师使用问题串进行教学的方法，称之为“问题串”教学法．以往关于“问题串”教学法的研究，更多的关注了“问题串”本身，包括其理论基础[1~4]、在教学中如何设置[5]以及如何在某个具体的教学内容下高效使用[6~7]“问题串”教学法，却鲜有从教师的角度审视“问题串”教学法的研究．那么，新手型教师与经验型教师对具体“问题串”教学法案例的评价有无差异？新手型教师与经验型教师问题串编制的侧重点是否相同？

2 研究方法

2.1 问卷的编制

在编制调查问卷之前，首先查阅了“问题串”教学法的相关文献，精心选取了初高中两个不同课型的“问题串”教学法的案例，先后请一位数学教育研究专家和两位一线高中数学教师进行审阅．接着，在十位一线的高中数学教师中进行了预测，经过反复修改，最终定稿了“有关‘问题串’教学法的调查（教师问卷）”．

2.2 被试与问卷收发情况

选取100位2014年9月参加在江苏扬州举办的江苏省高中学科（数学）教师提高培训的高中数学教师作为被试，他们分别来自扬州、泰州、宿迁和镇江4个大市．共发放问卷100份，回收85份，其中有效问卷81份，回收率和有效率分别为85%和81%．这81位高中数学教师的基本情况如表1所示．

研究规定教龄在1~5年或者教龄在6~15年且专业技术职称为中教二级的被试称为新手型教师；教龄在15年以上或者教龄在6~15年且专业技术职称为中教一级及以上的被试称为经验型教师．据此，回收的有效问卷中，新手型教师有25人，经验型教师有56人．所占比例分别为30.9%和69.1%．

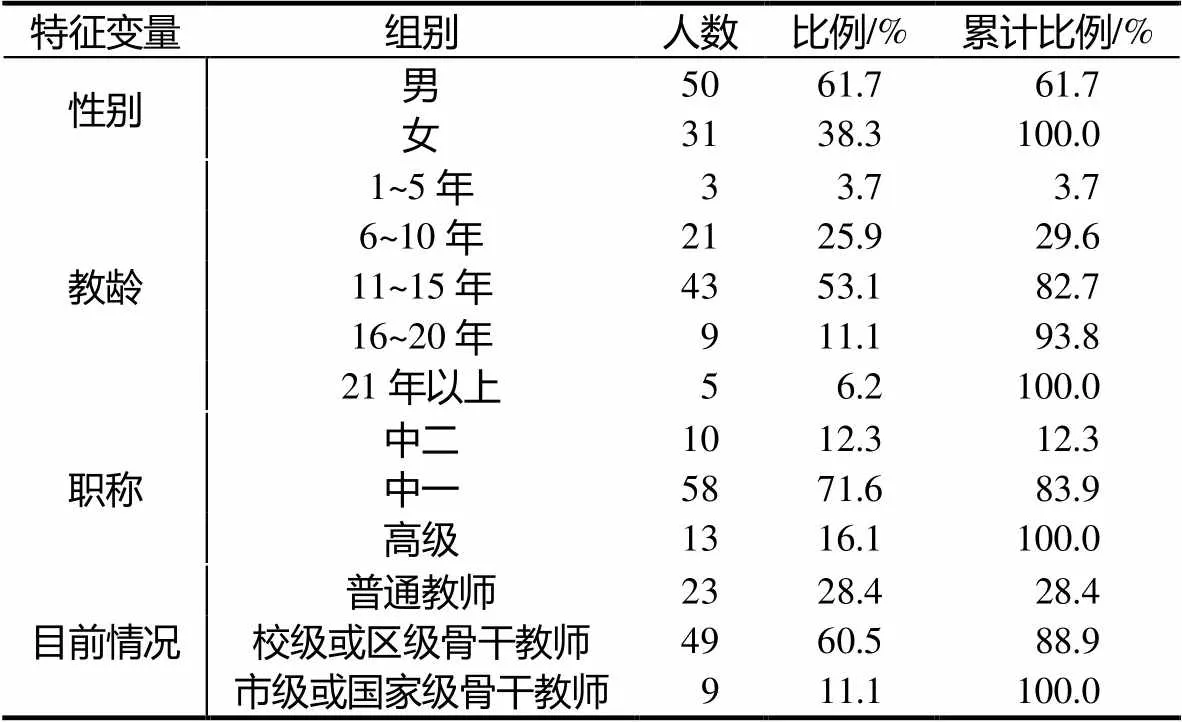
表1 被试基本情况（N=81）

3 结果与分析

3.1 两种教师对具体“问题串”教学法案例评价的差异

问卷给出了初高中数学教学中的两个案例，需要教师对案例中的问题串设计进行“好、合格、不好”的评价，并给出理由．其中案例一为同一课题的两种不同问题串设计，涉及概念和命题的教学以及探究活动；案例二涉及解题和试卷讲评的教学．

3.1.1 对案例一的评价

案例一：平行四边形的性质探索[8]

设计一：

问题一：将一张平行四边形纸片沿一条对角线剪下，得到两张三角形纸片，它们能完全重合吗？它们的边与角有什么关系？证明你的结论．

问题二：准备两张形状、大小完全相同的平行四边形透明纸片，折出它们的两条对角线，将它们重合放置在桌面上，并用一枚大头针固定在对角线交点处，下面的纸片保持不动，将上面的纸片绕着大头针旋转180度，观察它们是否重合．由此你能发现在一个平行四边形中，还有哪些线段是相等的？证明你的结论．

设计二：

将一张纸对折，剪下两张叠放的三角形纸片．将它们相等的一组边重合，得到一个四边形．

问题一：你拼出了怎样的四边形？与同伴交流．

问题二：在拼接得到的平行四边形中，有哪些相等的线段、相等的角？你是如何得到的？与同伴交流．

问题三：平行四边形的两条对角线、相交于点．图形中有哪些三角形是全等的？有哪些线段是相等的？设法验证你的猜想．

经过SPSS 21.0的统计分析，得到两种类型教师对案例一中两种问题串设计的评价情况如表2、表3所示．

表2 两种类型教师对问题串设计一的评价

Kolmogorov-Smirnov检验结果为=0.344，=1.000>0.05，说明在0.05显著性水平上新手型教师和经验型教师对于问题串设计一的评价差异不显著．

表3 两种类型教师对问题串设计二的评价

Kolmogorov-Smirnov检验结果为=0.716，=0.685>0.05，说明在0.05显著性水平上新手型教师和经验型教师对于问题串设计二的评价差异不显著．针对上述结果，由于新手型教师与经验型教师的评价差异不显著，因而研究者将教师对两种问题串设计的评价较为集中的理由进行了归类，如表4所示．

表4 案例一两种问题串设计评价理由表

从表4可以看出，涉及概念、命题的探究活动问题串设计，无论是新手型教师还是经验型教师均表示应让学生动手操作、自主探究，从而激发学生兴趣、调动学生的思维，让学生“在数学学习中承担更大的责任”[9]；在问题串的叙述上，两类教师认为文字叙述不宜过多，问题的指向性不能太强，即每一个问题指向教师设计好的数学知识与结论，学生完成教师预设的“规定动作”，学生在看似热闹的操作中却没有得到思维上的提升，很容易产生“滑过现象”[10]，这样的问题串设计有待商榷；在问题串本身的可操作性上，应尽量降低偏离探究主题的情形，探究活动的结果在很大程度上决定了学生对于新数学知识或结论的“第一印象”，教师应在学生操作的过程中适当加以引导，提高学生探究活动的有效性．

同时，在对案例一的评价中，还意外发现部分新手型教师对于初中学生的数学学习不够了解，提出了“研究平行四边形的性质，根本不需要去拼平行四边形，直接给出定理即可”、“探究活动只适合理解力、观察力、逻辑推理能力强的学生，差的学生只能看热闹”等看法；其次，部分新手型教师不熟悉初中数学教材的编排，如有的教师提出“学生在学习平行四边形之前还没有学习过三角形，因此设计二是不符合学生的认知规律的”．

3.1.2 对案例二的评价

案例二：一道习题的讲评[11]

教师：所以这道题可以通过什么方法来处理？

学生：数形结合．

学生：斜率为1．

……

学生：用导数．

……

经过统计分析，新手型教师与经验型教师对于案例二的问题串设计评价如表5所示．

表5 两种类型教师对案例二的评价

Kolmogorov-Smirnov检验结果为=1.791，=0.003<0.05，说明在0.05显著性水平上新手型教师和经验型教师对于问题串设计二的评价差异显著．

整理两种类型的教师对于案例二评价较为集中的理由，如表6所示．

从表5、表6可以明显的看出新手型教师和经验型教师对于案例二的评价有着明显的分歧．超过半数的新手型教师认为该案例的问题串设计好，问题环环相扣、体现数形结合的思想，激发了学生的思维，少部分新手型教师认为问题取代了学生的思考，跨度不大；经验型教师则几乎一针见血地指出该问题串设计思维力度不够，问题多、叙述啰嗦，没有揭示该题涉及的数学知识与数学思想等问题．

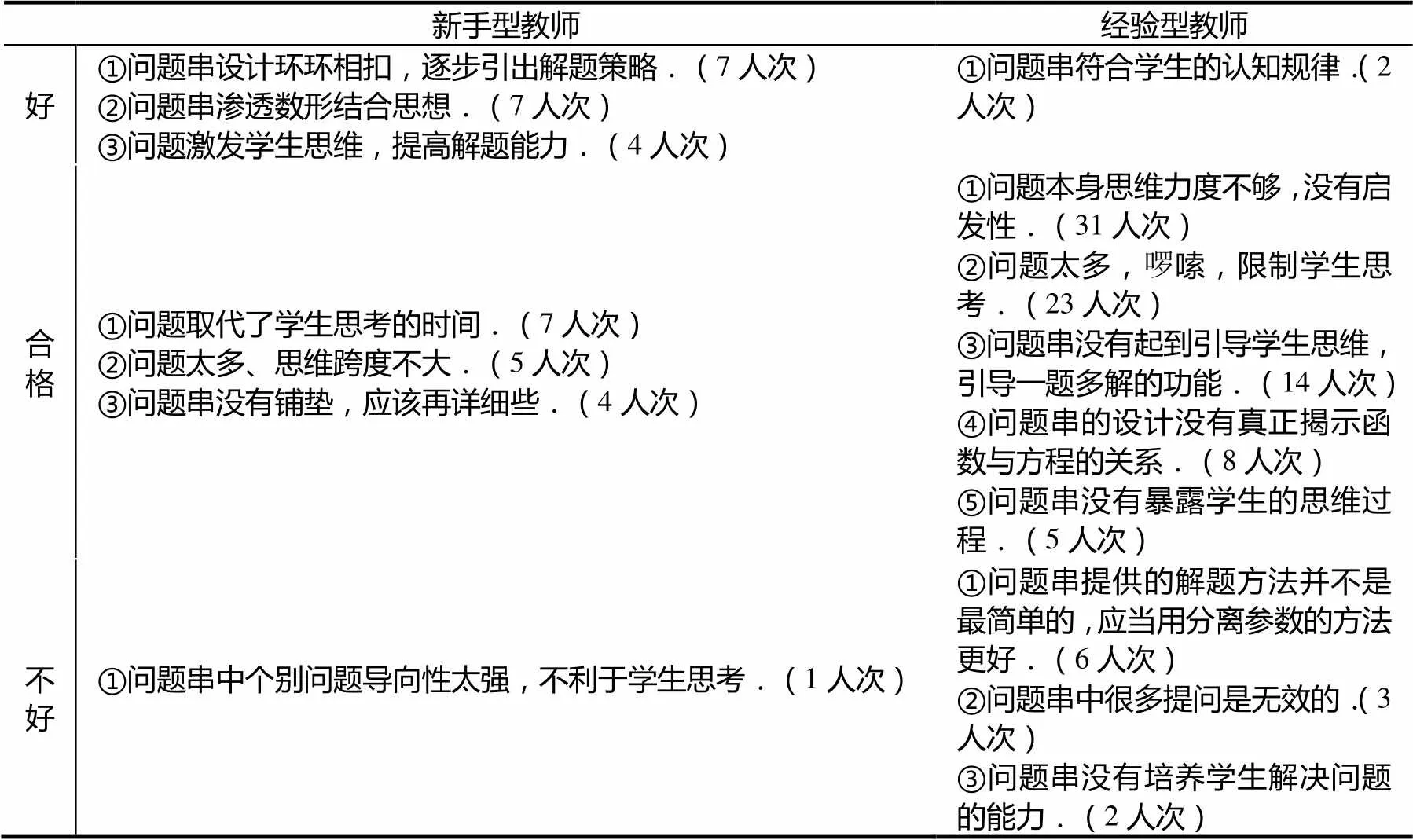
表6 案例二评价理由表

不仅如此，还有近二十位经验型教师给出了案例二问题串的改进意见．较为集中的几条如下：意见一，该题较为简便的方法是分离参数，再引导学生进行数形结合，同时应注意解法的可操作性；意见二，应先让学生自己分析题目，提出问题，解决问题，若没思路，教师可以适当提示，再引导学生有无其他解法；意见三，教师应围绕鼓励学生说出自己想法、询问为何想到该法、有无其他方法以及各种解法之间有无优劣之分进行问题串设计．新手型教师中仅有一位教师提出问题串应当引导学生探究函数零点、方程根之间的关系．

3.2 新手型教师与经验型教师问题串编制的侧重点

问卷的最后一个部分要求教师编制“等比数列前项和”的主体部分问题串，并给出编制的理由，该部分调研教师编制问题串的侧重点，经过整理得到较为集中的4种问题串设计．

设计一：

引入故事：国王奖励棋手麦子的故事，棋手要求在第一格放1粒麦子，第二格放2粒麦子，第三格放4粒麦子，以后每一个小格放的麦子是前一格的两倍，要摆满64格需要多少粒麦子？

问题四：这种方法的特点是什么？（引出错位相减）你能仿照上述问题的解法求出一般情形的结果吗？

问题五：你能仿照上述方法求出更一般的等比数列的前项和吗？

理由：问题串由数学历史小故事引入，激发学生的求知欲与兴趣；循序渐进，由具体到抽象，由特殊到一般，由易到难，层层递进，符合学生的认知规律；培养学生猜想解决问题的思路．

设计二：

问题一：你能求

问题二：根据上述求和过程，你有什么发现？

问题三：你能仿照该求和方法，求出

问题四：你能仿照上述方法求出更一般的等比数列的前项和吗？

理由：遵循从简单到复杂的原则，让学生能首先通过各种途经得到结果，逐渐归纳出公式，并能对公式进行有效的思辨．

设计三：

问题二：请参看课本，你有什么方法？

问题三：课本中为什么要乘以一个常数？这个常数是什么？怎么化简的？

问题四：为什么要讨论公比？你能用公式解决吗？

问题五：请你叙述错位相减法的步骤及公式使用的注意事项．

理由：让学生先思考再看书，让学生进行尝试，猜想出解题的思路，问题串的设计不能简单地给学生定下目标，而应起到给学生提供台阶的功能，至于怎样攀爬，应由学生决定．

设计四：

问题一：等差数列和等比数列的特征量有哪些？

问题三：回顾等比数列的定义，我们将前项和乘上一个公比，你发现与原来的式子有什么联系？

理由：由复习等差数列的特征量引入，由学生熟悉的知识过渡到陌生的知识，运用类比，符合学生的认知规律．

上述两种设计的教师人数及比例如表7所示．

表7 两种类型教师问题串设计人数及比例

如果将以上4种问题串设计称为“主流的”问题串设计，那么56位经验型教师中有49位给出了“主流的”问题串设计，占87.5%；而25位新手型教师中仅有11位，比例仅为44%，约为经验型教师比例的一半．

每一种问题串设计中，经验型教师的比例均高于新手型教师．由此可以初步推断出经验型教师的问题串编制能力要强于新手型教师．

具体看“等比数列前项和”这个内容，课标要求“探索并掌握等差数列、等比数列的通项公式与前项和的公式．”“等差数列和等比数列有着广泛的应用，教学中应重视通过具体实例（如教育贷款、购房贷款、放射性物质的衰变、人口增长等），使学生理解这两种数列模型的作用，培养学生从实际问题中抽象出数列模型的能力．”4种问题串设计都较好地贯彻了课标的要求，侧重教学的重难点．

在编制问题串的过程中，经验型教师比新手型教师更加注重：（1）激发学生的学习兴趣．设计一中“国王奖励棋手麦子”的数学历史小故事，拉近了与学生的距离，提升学习内驱力；设计二中3个简单的计算式子，贴近学生的“最近发展区”，给学生展示与成功的机会，激发学生的求知欲；（2）驱动学生“回归课本”．设计三充分体现了教材的重要性，学生并不是不加思考地去教材中找答案，而是在思考了教师给出的问题后，带着自己的见解去解读课本，学生会为自己的想法与教材不谋而合而喜悦，也能受到教材的启发；（3）将知识点进行“串联”．设计四体现了数学作为一门系统性强的学科，知识点之间相互联系，很多知识点在整个高中数学知识体系中起着承上启下的作用，同时侧重从学生已经学过的知识引入，过渡十分自然，符合学生的认知规律．

4 调查结论

4.1 两种类型教师对不同课型的问题串设计评价存在差异

新手型教师与经验型教师对涉及概念命题的探究课问题串设计（案例一）评价差异不显著（=0.344，=1.000>0.05；=0.716，=0.685>0.05），但暴露出部分新手型教师不熟悉初中数学知识体系和教材．

新手型教师与经验型教师对解题或者试卷讲评课（案例二）的评价差异显著（=1.791，=0.003<0.05），暴露出新手型教师对于解题、数学知识本身的理解与经验型教师存在差异．

与此同时，对案例二的评价与改进中，经验型教师在解题或者试卷讲评课上的表现要优于新手型教师，体现在：（1）追求一题多解，引导学生思辨各种解法之间的差异；（2）教学理念新，倡导学生为主体，教师作为引导者、合作者的教学理念，鼓励学生表达己见；（3）思考有深度，对于具体的案例，经验型教师的思考不是停留在问题层面，而是高中数学课程的宏观视角加以审视，提出的意见一针见血，改进意见中肯有效．

4.2 经验型教师编制问题串的能力强于新手型教师

在4种“主流”问题串设计中，经验型教师的比例（87.5%）远远高于新手型教师（44%）．4种“主流”的问题串设计体现出了好的问题串标准：紧密围绕教学内容、适合学生的特点．经验型教师在编制问题串的过程中比新手型教师更加注重激发学生的学习兴趣、驱动学生“回归课本”以及将知识点进行“串联”．新手型教师处于模仿与提出问题串的层面上，经验型教师能够深入到策略的层面．体现出经验型教师编制问题串的能力强于新手型教师．

此次调查也体现了一些经验型教师的教学智慧，如有一位教师在给出“国王奖励棋手麦子”的例子后，诙谐地问学生：“如果你是国王，你会怎么处理这个尴尬的局面？如果我是国王，我就让棋手用袋子将麦子装走，如果装不走，就不给奖励．”学生“在数学情境中观察、分析，产生疑虑、困惑，逐步发现于形成解决数学问题的意识．”[12]

4.3 教师对问题串的评价能力与其编制研究能力相互影响

在对案例二的评价中，许多新手型教师给出了与经验型教师大相径庭的评价，认为该问题串的问题环环相扣、体现数形结合的思想，激发了学生的思维．将这7位新手型教师的问卷再次进行了分析，发现7位教师对于案例的评价都是简单的几句话：“好，从思想方法上找突破”、“符合学生认知结构”、“问题引入好”……同时还发现有两位教师在案例一与案例二的评价中至少有一个问题串设计没有给出评价，有两位教师没有给出“等比数列前项和”的问题串设计，在剩下的3位教师中有一位教师给出了“国王奖赏棋手麦子”的设计，其他两位教师仅仅将问卷中给出的一个问题串设计样例进行了简单修改，没有给出个性化的设计．

以上研究结果在教师实践层面上也验证了庄志刚[5]、郑建元[13]、罗增儒[14]、李渺[15]等人的研究结论．

5 提升新手型教师设计问题串能力的策略

5.1 提高把握数学本质的能力

新手型教师对于不同课型的问题串评价与经验型教师存在差异，体现新手型教师对于数学本质的把握还不够．针对不同的课型，新手型教师都应当厘清数学的本质．数学的产生与发展的过程是发现问题、分析问题、解决问题的过程，数学教师的根本任务是还原这个过程，挖掘隐藏在书本知识背后的思想与方法[16]．数学课主要有概念课、原理课和解题课3种课型．

概念课，新手型教师应当认识到数学概念是反映数学对象的本质属性，既要静态的分析其定义形式，更需要在比较、变化等联系活动中揭示其内涵[17]；原理课，应当教会学生了解定理的来龙去脉，积累数学史知识[18]；解题课，应当教会学生如何思考问题，怎样由已知推向未知，通过变式教学提升学生的思维．

只有针对不同课型，有的放矢地编制问题串，才能从本质上提升新手型教师编制问题串的能力．

5.2 优化问题串设计

经验型教师在编制问题串时比新手型教师更加注重激发学生的学习兴趣、驱动学生“回归课本”以及将知识点进行“串联”．从中可以看出，好的问题串应当符合两大标准．一要紧密围绕教学内容，二要适合学生的特点．

数学教学本身是将学术形态的数学知识“激活”，转化为教育形态的知识的过程．新手型教师在进行问题串编制时首先应当宏观把握数学课程体系、熟知教材内容，然后紧扣教学内容，想方设法地调动学生学习数学的积极性、同时注重对学生思维的训练，最终提炼出数学思想方法，从而完成一整套的有效教学．

5.3 及时更正设计理念

新手型教师不能对问题串设计案例给出有效的评价，尤其像需要教学经验积累的解题或者试卷讲评课上，新手型教师的想法相比经验型教师就存在较大差距．同时，部分经验型教师给出案例二的改进建议，充分体现了经验型教师问题串设计理念新，思考有深度，这点与左坤[19]、李鹏[20]、徐利[21]、王光明[22]的研究基本吻合．

新手型教师应当主动加强与经验型教师的沟通交流，虚心听取经验型教师的合理化建议，及时更正设计理念．

[1] 曾峥，杨之．“化归”刍论[J]．数学教育学报，2001，10（4）：38-41．

[2] 陈艳斌，朱维宗，吕传汉．数学“情境与提出问题”教学与RME教学之比较研究[J]．数学教育学报，2006，15（4）：59-60．

[3] 张奠宙．中国数学双基教学理论框架[J]．数学教育学报，2006，15（3）：1-2．

[4] Martin A. Simon, Ron Tzur. Explicating the Role of Mathematical Tasks in Conceptual Learning: An Elaboration of the Hypothetical Learning Trajectory[J]., 2004, 6(2): 91-104.

[5] 庄志刚．合理设置激发思维——例谈“问题串”在数学教学中的设置[J]．中学数学杂志，2014，（5）：7-9．

[6] 王飞．从一节解析几何复习课管窥数学问题串教学法[J]．中学数学月刊，2014，（5）：36-37．

[7] 张彦春，李长毅，徐宏伟．职前数学教师教学过程设计的问题与思考——基于“平行线性质”教学过程设计的同课异构个案分析[J]．数学教育学报，2014，23（3）：35-39．

[8] 顾继玲，张新华．初中数学教材探究活动设计的思考[J]．数学教育学报，2012，21（3）：63-66．

[9] 郑毓信．“问题解决”与数学教育（2008）[J]．数学教育学报，2009，18（1）：1-4．

[10] 宁连华．数学探究教学设计研究[J]．数学教育学报，2006，15（4）：40．

[11] 王慧清．一道习题讲评五种教学设计的辩证思考[J]．中学数学（高中版），2014，（6）：22-24．

[12] 常磊，夏小刚，吕传汉．数学“情境—问题”教学中教师的MPCK理论研究[J]．数学教育学报，2012，21（5）：67-71．

[13] 郑建元．初中数学“情境—问题”教学的校本化研究——“用同边长的正多边形拼地板”教学案例[J]．数学教育学报，2009，18（1）：99-102．

[14] 罗增儒，罗新兵．作为数学教育任务的数学解题[J]．数学教育学报，2005，14（1）：15．

[15] 李渺，陈长伟．高效数学课堂教学行为研究——基于优秀高中数学教师的个案研究[J]．数学教育学报，2010，19（5）：80-83．

[16] 何勇，曹广福．数学课堂如何兼顾学生数学素养与应试能力[J]．数学教育学报，2014，23（2）：60．

[17] 李祎．高水平数学教学到底该教什么[J]．数学教育学报，2014，23（6）：32．

[18] 罗新兵，刘阳，安德利亚斯．数学史融入数学教学研究的若干思考[J]．数学教育学报，2012，21（4）：20-23．

[19] 左坤．初中数学教师教学设计能力研究[J]．数学教育学报，2011，20（2）：41-44．

[20] 李鹏，傅赢芳．论数学课堂提问的误区与对策[J]．数学教育学报，2013，22（4）：97-100．

[21] 徐利．杜郎口模式下的数学课堂教学[J]．数学教育学报，2013，22（2）：99-102．

[22] 王光明．高效数学教学行为的特征[J]．数学教育学报，2011，20（1）：35-38．

Investigation and Study on the Evaluation and Formation of Problem-Chain of High School Mathematics Teachers

GAO Xiang, ZHANG Bo

(College of Mathematics and Science, Yangzhou University, Jiangsu Yangzhou 225002, China)

On the evaluation of designing different types of mathematical classes’ problem-chains, there are obvious differences between novice teachers and experienced teachers in terms of problem-solving or examination paper analysis. However, not clear in the concept of teaching. The experienced teachers are better than novice teachers in problem solving and mathematics knowledge understanding. Experienced teachers pay more attention to designing problem-chains, such as breaking through the important and difficult points in teaching, making knowledge “series”, stimulating students’ interests in learning and driving students to “return of textbooks” etc. At the same time, there is an interrelationship between teacher’s evaluation and formation ability of problem-chains.

novice teachers; experienced teachers; problem-chain; evaluation

[责任编校：陈隽]

G633

A

1004–9894（2016）03–0066–05

2016–01–09

中国学位与研究生教育学会课题——密西根州立大学教育硕士培养的案例研究（B2-2013Y09-137）

高翔（1990—），男，江苏金坛人，硕士生，主要从事数学教育研究．