基于AUC统计量的随机森林变量重要性评分的研究*

哈尔滨医科大学卫生统计教研室（150081） 张晓凤 侯 艳 李 康

基于AUC统计量的随机森林变量重要性评分的研究*

哈尔滨医科大学卫生统计教研室（150081） 张晓凤 侯 艳 李 康△

随机森林（random forest，RF）［1］是高维组学数据常用的分析方法，在进行判别分析时，同时能够给出变量重要性评分（variable importance measure，VIM）。RF的变量重要性评分通常有两种，一种方法是通过变量值的置换计算其重要性，第二种方法是通过基尼（Gini）指数计算其重要性，由于置换法比Gini指数法具有更好的非偏倚性能，因此多采用置换法进行变量筛选［2－5］。然而，当数据类别（标签）比例不均衡时，即收集到的数据在两类中的数目不相同，尤其比例相差较大时，基于错误率（error rate，ER）的置换法不能准确反映变量的重要性。为此，Janitza等（2013）提出基于AUC统计量的评价方法，能够克服类别间比例不平衡的影响［6］。本文在简要介绍该方法的基础上，通过模拟实验和实例数据探索其适用性，并与传统的置换法进行比较。

原理与方法

1.RF的基本思想

RF采用组合方法（ensemble method）的思想，即对样本数据进行多次随机抽样产生N（通常为Ntree）个训练样本构造N棵分类树（称基分类器），在每次基分类器构建过程中，将训练样本以外的数据作为测试数据，称为袋外数据（out of bag data sets，OOB），并通过错误率来评价基分类器性能，最后根据投票（vote）准则将基分类器组合为一个RF分类器。RF在构建分类器的过程中，通过对变量重要性排序进行变量重要性评分。

2.基于错误率的置换方法

基于错误率置换方法的变量重要性评分（VIM＿ER），其基本原理是用同时随机置换各变量值，通过计算置换前后的OOB错误率间的差异衡量该变量的重要性。具体地，欲获得变量Xi的重要性评分，首先基于训练样本构建随机森林，并估计所有OOB样本的错误率，然后对所有OOB样本中的变量Xi值进行打乱获得新的袋外数据（OOB′），估算OOB′样本的ER，最后计算两次袋外数据的ER变化值。最后将所有OOB样本ER变化均值作为Xi的VIM，Xi的VIM定义如下:

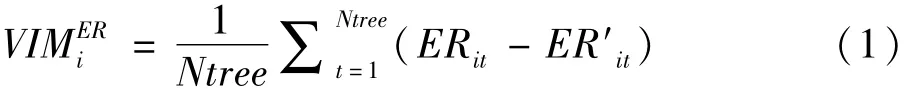
其中，Ntree为RF中树的个数，ERit为变量Xi置换之前第t棵树对应的错误率，ER′it为变量Xi置换之后第t棵树对应的错误率。

由VIM计算公式我们知道，如果变量Xi与标签（类别）无关联，随机置换该变量后对应的袋外数据错误率不会发生变化，理论上＝0；相反地，如果＞0，则说明变量Xi与分类是有关联的。

3.基于AUC统计量的置换方法

基于AUC统计量置换法同样能够得到变量的重要性评分（VIM＿AUC），与OOB错误率得到的VIM＿ER原理相似，两者区别在于后者基于错误率变化衡量变量重要性，前者则是基于AUC（ROC曲线下面积）值的变化评价变量重要性。这里，变量Xi重要性评分定义如下:

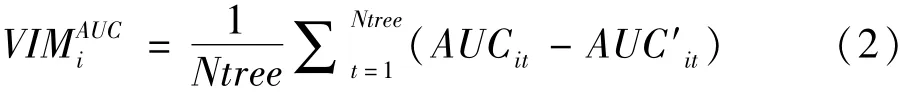
其中，AUCit为变量Xi置换之前第t棵树对应的AUC值，AUC′it为变量 Xi置换之后第 t棵树对应的 AUC值。

使用OOB错误率的变化作为评价变量重要性的指标时，考虑的是整体错误率变化情况，但最大的问题是当多数类样本较大时，OOB错误率未充分考虑少数类的错误率，相当于赋予了多数类更高的权重。基于AUC统计量的置换方法同时考虑灵敏度和特异度，相当于对两类各自的准确率赋予了相同的权重，直观上，对于类别间不平衡数据而言，基于AUC统计量得到的变量重要性评分更趋于合理。

模拟实验

1.实验目的

（1）探索处理不平衡数据时基于ER估计VIM的偏倚性，验证基于AUC统计量获得VIM的合理性。

（2）比较VIM＿ER和VIM＿AUC对变量排序的差别，以及对差异变量和噪音变量的区分能力。

2.实验设置

（1）模拟数据共设置65个自变量 X＝（X1，…，X65）和一个应变量Y∈｛0，1｝，其中按自变量与应变量之间的关联程度设置强、中、弱、无四个等级，共15个变量，称为差异变量；另外设置50个无关联变量，称为噪音变量，具体分布情况见表1。现设置，分组1为样本较少一组，分组2为样本较多一组；两组类别样本量不平衡的比例（n1∶n2）为 1∶1，1∶3，1∶5，1∶10，1∶15，1∶20；第一组的样本含量分别为10和30，实验重复100次。

（2）随机森林构建参数设置，分类树Ntree＝1000，mtry＝5，基分类器构建时抽取的训练数据为无放回抽样。

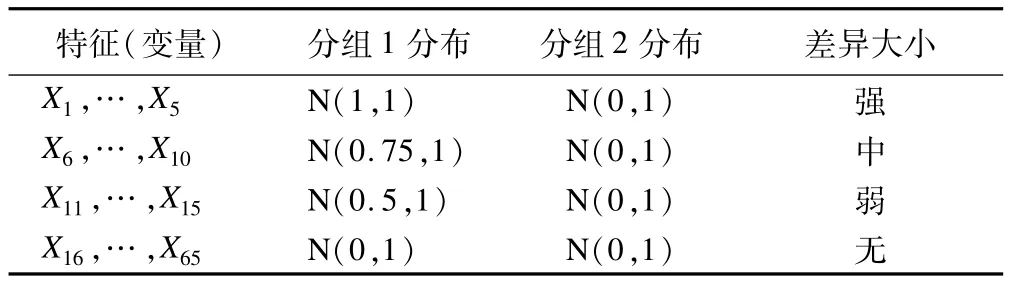
表1 自变量的分布参数设置

3.模拟实验结果

（1）图1和图2分别给出两组样本量平衡和不平衡情况下，VIM＿ER和VIM＿AUC两种方法的结果。图1结果显示，在两组例数相同时，VIM＿ER和VIM＿AUC两种方法均能真实反映变量重要性；图2结果显示，在两组例数不相同、并且相差较大时（n1∶ n2＝1∶20），VIM＿ER方法几乎看不到差异变量的作用，而VIM＿AUC方法能更好地区分出差异变量，比VIM＿ER方法更合理。

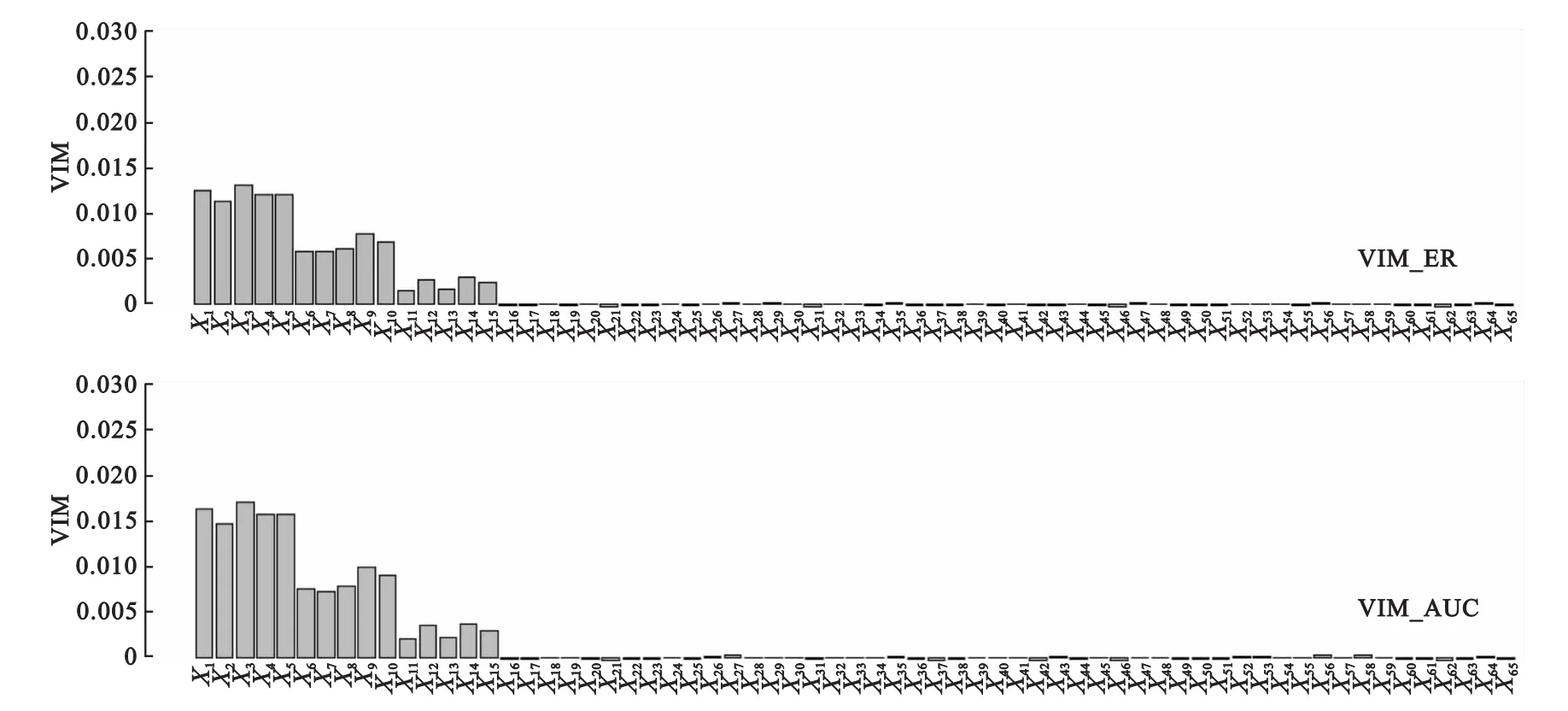
图1 两组样本量平衡（n1＝30，两组样本量比例为1∶1）

图2 两组样本量不平衡（n1＝30，两组样本量比例为1∶20）

（2）图3给出了两组样本量不相同情况下，VIM＿ER和VIM＿AUC两种方法区分差异变量的能力。结果显示，随着两组不平衡比例增加，VIM＿ER法对差异变量区分的AUC值呈下降趋势，表明两组样本比例不平衡时，VIM＿ER方法获得的变量VIM得分不能很好地识别差异变量；而VIM＿AUC法得到的AUC值随着总样本量的增加而增加，最后趋于稳定，表明VIM＿AUC不受两组样本例数不平衡的影响。

图4给出了在不同差异情况下，VIM＿ER和VIM＿AUC两种方法得到的结果。结果显示，差异不大和样本量较小时，两组不平衡比例对VIM＿ER的影响非常明显，而VIM＿AUC则能够更好地区分差异变量与噪音变量。

图3 VIM＿ER和VIM＿AUC两种方法区分15个差异变量的能力

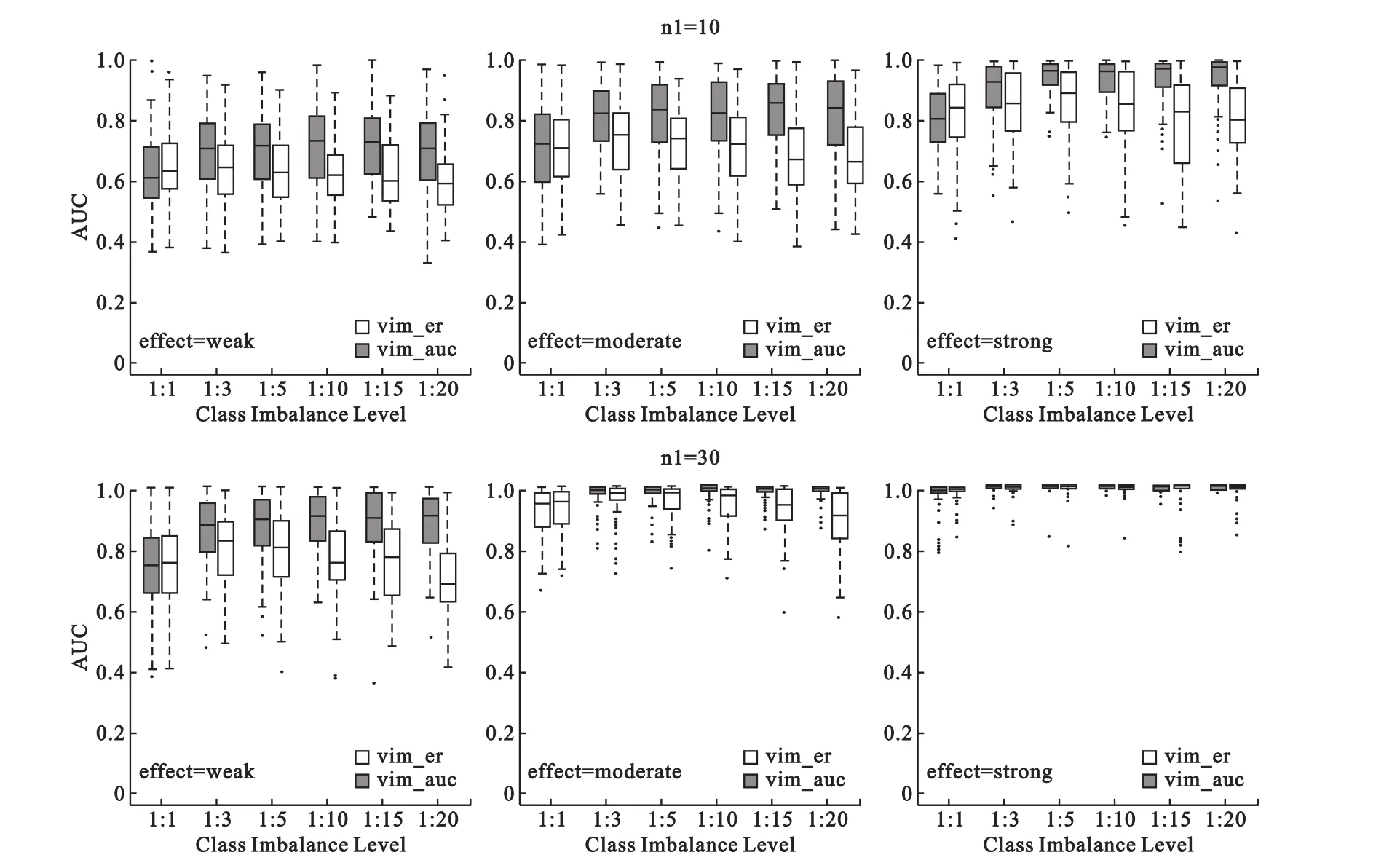
图4 VIM＿ER和VIM＿AUC两种方法区分5个不同差异变量的能力

实际数据验证

本文选取RNA编辑数据作为实际数据对上述两种方法进行比较。该数据共包含2613例样本，分为两组，其中1306例进行了 RNA编辑，1307例未进行RNA编辑，分析变量43个［7］。为评估 VIM＿ER和VIM＿AUC两种方法在不平衡情况下筛选变量的结果，对数据做以下处理:①随机打乱43个变量形成噪音变量，加入到实际数据中，从而共有43×2＝86个变量；②在第一组中随机抽100例，同时在第二组中抽取一定比例的样本，设置两组例数比值分别为1∶5和1∶10。以上过程重复100次，最后计算VIM得分的平均值。

图5分别给出了两组样本量平衡（1∶1）和不平衡（1∶5，1∶10）时，使用 VIM＿ER和 VIM＿AUC两种方法得到的结果。结果显示:两组样本量相同时，VIM＿ER法与VIM＿AUC法进行变量筛选后得到的VIM值排序基本相同；两组样本量不同时，随着两组不平衡程度的增加，使用VIM＿ER方法得到的VIM值中很多逐渐趋于0，而VIM＿AUC方法仍能给出相对准确的变量重要性评分，保持“差异变量”的VIM值相对较高，从而不会因不平衡问题改变变量的重要性排序。

讨 论

1.随机森林（RF）是由多个决策树（基分类器）组成的分类器，能够有效地处理非线性、交互作用、共线性以及高维等问题，同时还能够避免过拟合，可以进行预测和变量筛选［8］。在类别间例数不平衡时，实际经常使用的方法是在计算变量重要性时使用错误率，相当于对例数较多的类别赋予了更高的权重，从而导致这种方法估计VIM时出现明显的偏倚，这在实际应用中应予注意。

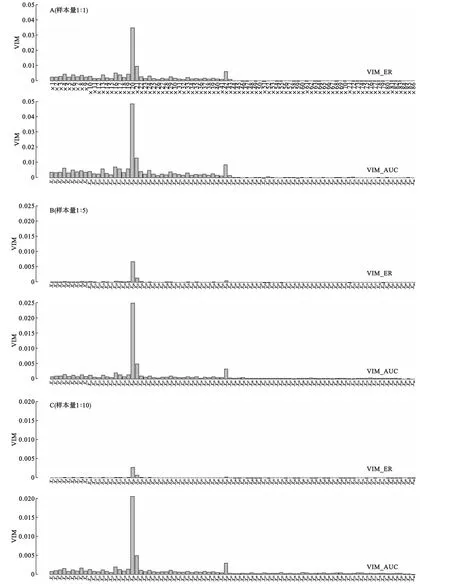
图5 两种方法的变量重要性评分（A图1∶1，B图1∶5，C图1∶10）

2.在构建RF分类器时，使用AUC统计量计算VIM值，能够在样本例数不平衡时准确地反映变量的作用。模拟实验和实际数据验证的结果显示了这种方法可以有效地解决不平衡的问题。

3.不平衡的问题主要出现在前瞻性研究中，比如癌症患者远远少于健康人群。这种情况下，虽然可以使用巢式病例-对照的方法，但是如果数据完整，直接分析全部数据效果会更好，这时可以使用VIM＿AUC方法进行变量筛选。

4.VIM＿AUC方法也有一定的局限性，即AUC这一指标有时不够敏感，因此今后也可以考虑使用部分ROC曲线下面积、信息量等其他统计量构建RF分类器。

［1］Breiman L.Random Forests.Machine Learning，2001.45（1）:5-32.

［2］Calle M L，Urrea V.Letter to the Editor:Stability of Random Forest importance measures.Briefings in bioinformatics，2011，12（1）:86-89.

［3］Strobl C，Boulesteix AL，Zeileis A，et al.Bias in random forest variable importance measures:Illustrations，sources and a solution.BMC bioinformatics，2007，8（1）:25.

［4］Boulesteix AL，Bender A，Bermejo JL，et al.Random forest Gini importance favours SNPs with large minor allele frequency:impact，sources and recommendations.Briefings in Bioinformatics，2012，13（3）:292-304.

［5］Nicodemus KK.Letter to the editor:on the stability and ranking of predictors from random forest variable importance measures.Briafings in Bioinformatrics，2011，12（4）:369-373.

［6］Janitza S，Strobl C，Boulesteix AL.An AUC-based permutation variable importance measure for random forests.BMC bioinformatics，2013，14（1）:119.

［7］Cumm ings MP，Myers DS.Simple statistical models predict C-to-U edited sites in plantmitochondrial RNA.BMC bioinformatics，2004，5（1）:132.

［8］李贞子，张涛，武晓岩，等.随机森林回归分析及在代谢调控关系研究中的应用.中国卫生统计，2012（6）:158-160，163.

国家自然科学基金资助（81473072）

△通信作者:李康，E-mail:likang@ems.hrbmu.edu.cn

（责任编辑:郭海强）