基因组学数据整合中的批次效应移除算法*

哈尔滨医科大学卫生统计教研室（150081） 陈天成 侯 艳 李 康

基因组学数据整合中的批次效应移除算法*

哈尔滨医科大学卫生统计教研室（150081） 陈天成 侯 艳 李 康△

微阵列的基因表达谱已经成为研究癌症细胞转录的重要工具，且成功用于许多肿瘤识别和与癌症相关的生物标志物研究［1－2］。然而，实际中需要大量的样本才能够得到稳定的分析结果，而由于实际的复杂程度及费用问题，每个数据集的样本量受到了限制。为此，可以将已公开的微阵列数据整合，在减少花费同时提高结果的稳定性。

研究者在数据整合过程中常面对由于平台设计、合成及探针注释不同带来的跨平台基因表达研究的难题［3］。另外，同一方面的微阵列实验研究可能在不同时间或地点进行，其系统误差会给数据整合带来困难。上述系统误差在文献上称之为批次效应（batch effect）。Scherer和Andreasd将批次效应定义为样本在不同批次处理和测量中系统上的技术差异［4］。当批次效应引入的误差足够强以至于混杂真实的生物学差异时，未经移除批次效应的数据分析可能出现误导性的结果［5］。微阵列信号强度的归一化（normalization）是一种标准化分析技术，如MAS5和RMA方法，但这是一种在特定数据集内部的标准化方法，无法移除批次效应［6］。如何合理有效地移除批次效应是目前基因组研究的热点之一，本文将对此做一探讨。

统计分析算法

基因组学中数据批次效应移除的整合算法很多，本文主要介绍目前已经明确有较好效果［7－8］及新近提出的方法。

1.经验贝叶斯方法

经验贝叶斯（empirical Bayes）［9］方法的思想是从基因和实验条件中使用“先验信息”，期望利用先验信息得到更好的估计或者更稳定的推断。模型的假设是基于位置和尺度的调整，形式如下:

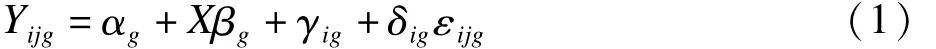
其中，Yijg是批次 i（i＝1，2，…，b）、样品 j（j＝1，2，…，ni）和基因 g（g＝1，2，…，mi）的表达值，αg是基因 g的平均表达值，X是样品条件的设计矩阵，βg是对应X的回归系数的向量；误差项 εijg假设服从 N（0，σg）；γig和δig表示批次i中基因g加法和乘法的批次效应。

△通信作者:李康，E-mail:likang@ems.hrbmu.edu.cn

算法分为三步:

（1）标准化数据，即通过基因表达数据，用最小二乘法和约束条件∑ini＝0得到估计值和，方差估计为

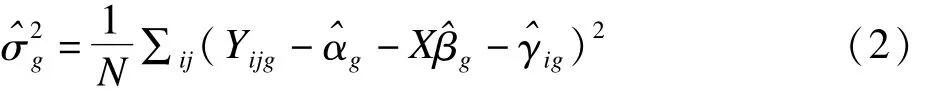
再通过下式把标准化数据Zijg计算出来，即

（2）估计批次效应参数。假设 Zijg～N（γig，δig），采用参数先验或者非参数先验方法计算出批次效应估计值和。其中参数先验方法要求 γig～N（γi，）及～InverseGamma（λi，θi）。

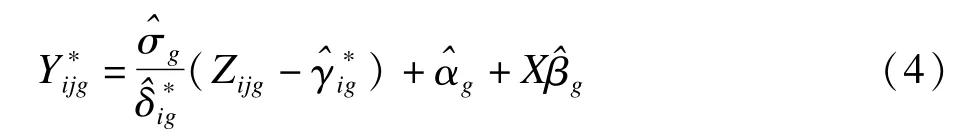
2.改进ComBat方法

改进ComBat［10］是前述经验贝叶斯方法的改进方法，该法通过改变参数的估计值及为批次水平的估计值及，实现把样本转换到“金标准”参考批次的均数和方差，而不是总均值和合并方差。标准化数据表示如下:

最后批次效应调整数据中使用的均值和方差估计值通过参考批次的参数估计值进行估计。

M-ComBat调整的数据可由下式计算得到，即

其中符号的意义同式（4）。

3.跨平台归一化

跨平台归一化（cross-platform normalization，XPN）方法［11］，其基本思想是识别在两个研究中具有相似表达特征的基因和样本的同质性区组。数据模型构建基于简单区组线性模型，即对于每个基因，其表达式如下:

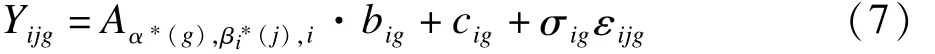
其中Yijg为批次 i、样品 j和基因 g的观测值，α*:｛1，…，m｝→｛1，…，K｝和:｛1，…，ni｝→｛1，…，L｝，i＝1，2分别为聚类后的基因和样本的组别，Aα*（g），β*i（j），i是区组的均数，big和cig分别表示不同批次和特定基因的灵敏度及偏移参数，噪声变量εijg是相互独立的标准正态分布。

算法首先对研究数据进行样本标准化和中心化，然后采用k-均值聚类法分别对样品和基因聚类，给出分配函数α和β。进而，对函数αg和βi（j）使用极大似然方法得到模型参数的估计值，各次聚类后基因表达值为

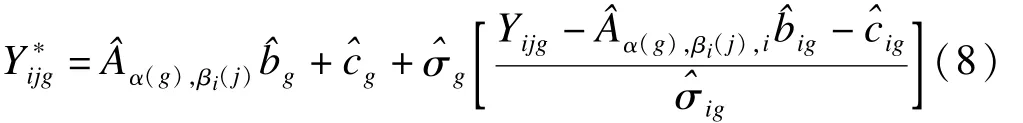
上述过程需要进行30次，算法的输出结果是重复运行获得的归一化平均值。

4.平台独立的LDA模型

平台独立的LDA（platform independent LDA，PLIDA）模型［12］，假设不存在批次引起的差异，不同批次的基因表达芯片获得的数据能够合并在一起进行分析。基于此假设，该方法通过同时学习主题模型分解实现跨批次归一化，该分解过程描述了来自所有批次数据的归一化及每个批次使用调整因子进行校正。其建模思想与潜在狄利克雷模型（latent Dirichle tallocation，LDA）［13］相似。该模型可用图1表示，其中图中的阴影圈表示可观测变量，非阴影圈表示潜在变量。这里，tm表示基因表达水平（拷贝数），θ表示基因表达水平不同的概率分布是批次和特定基因的调整因子，为基因g在离散化表达水平z时的概率，即＝P（g＝z）。

图1 PLIDA模型的图解模型

上述模型参数可以用模型（9）进行估计，即对于第i个批次的第j个样品，在离散化基因表达水平z（z∈｛1，2，…，K｝）情况下有概率模型:

在该等式中，左侧表示所有基因增加1个拷贝数属于基因g的概率，右侧中的fig是批次和特定基因的调整因子，该因子调整在离散化基因表达水平πz下基因g拷贝数的概率。假定模型中的先验概率关系如下:

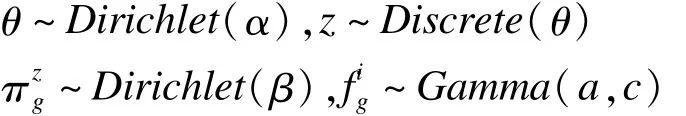
其中c＝1/a。通过块共轭梯度下降的方法使得后验对数似然比最大化，从而估计出模型参数｛｝，…，｛｝，｛θ1｝，…，｛θK｝，｛α｝和｝，…，｛，最后得到调整后的基因表达值

5.基于比值的方法

基于比值的方法（ratio based method）［5］以各自批次的单个（或一组）参考样品为基础调节样品的基因表达值。该方法假定参考样品中的基因与剩下样品的具有相同的批次效应，因此通过减去对应批次的参考样品的每个基因平均值来移除批次效应。这里把第i个批次中第j个参考样品中的第g个基因表达值用表示，第i个批次的参考样品数量为ni。如果参考样品数ni≥1，则可以使用参考样品中的算数均数或者几何均数的基因表达值。两种方法如下:

（1）基于算术均数比值方法（Ratio-A）

（2）基于几何均数比值方法（Ratio-G）

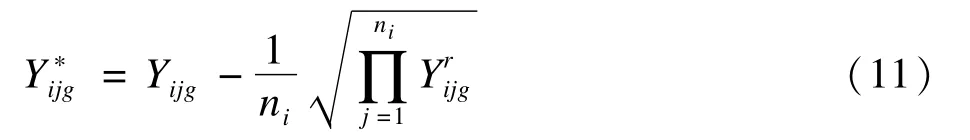
其他的统计算法还包括均值中心化［14］、基因标准化［15］、分位数离散化、中位数秩分数［16］等，具体可以参阅相关文献。

批次效应移除的评价方法

目前文献中将移除批次效应评价方法归纳为两种:可视化方法及定量度量方法［17］。可视化方法假设不同批次中感兴趣的生物学变量的样本分布相同，该假设对于数据整合过程至关重要这也意味着，合并的数据集在病例及对照组样本上应当包含相似的比例，由于估计的参数具有不可比性，整个分析可能倾向于误导性的结果。基于这个假设，若无批次效应的存在，不同研究间相同基因的表达水平应当有相似的分布，如果相同的批次聚在一起则表明批次效应的存在。根据上述两种理想情况，可视化方法主要分为基因水平及综合水平。基因水平的可视化方法从单个基因水平上呈现出批次效应的局部可视化，常见方式为基因表达数据的箱式图和概率密度曲线图。而综合可视化工具提供样本水平批次效应存在的图形，常见方式为树状图，主成分图及相对对数表达图［18］。

尽管可视化手段只对批次效应移除算法的有效性进行粗略估计，但是能够对算法移除批次效应结果进行快速检查，因此这种方法是实际中最常见和最直接的方法。如果想要准确评价批次效应移除的效果，应当使用定量度量的方法，这里简要介绍3种:

1.Mattews相关系数

Mattews相关系数（Matthews correlation coefficient）是从诊断目的出发，通过跨批次的预测准确性评价批次效应移除效果的评价指标。其基本思想是，如果已经移除批次效应，则分类器的错误率理应下降。需要注意的是，预测准确性是高度依赖于分类比率的指标，当终点指标在研究中高度不平衡，结果可能使人误解。为此可以使用 Mattews相关系数（MCC）［5］，即

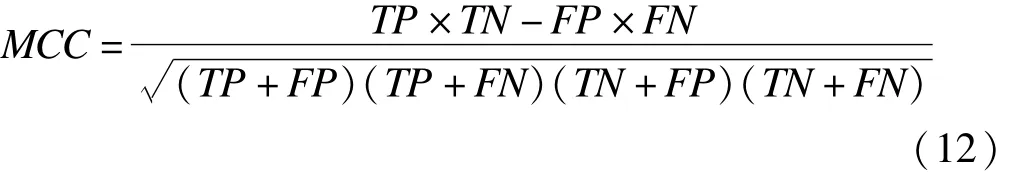
其中TP和FP表示真阳性和假阳性，TN和FN表示真阴性和假阴性。－1≤MCC≤1，1表示完全预测正确，0表示随机预测，－1表示预测结果完全相反。

2.混合分数

混合分数（mixture score）［19］的原理是，计算数据A的样品在数据B的k-近邻范围内的数目与数据B中样品数目k的比值。指标计算如下:

其中x是数据A的样品在数据B的k近邻范围内的数目，0≤Mixturescore≤1。实际中，分数愈接近0.5说明两个批次的数据整合愈好，而分数接近0或1则意味两个数据集整合不好。

3.校正兰德指数和信息变异

Saman指出目前定量评价方法通常不能同时满足以下两个标准:①技术因素引起的混杂信号应当从数据中移除（批次效应移除）；②感兴趣的生物学信号在批次校正算法后应该保持不变（生物学信号保留）。为此可以使用校正兰德指数和信息变异［20］。

（1）兰德指数

兰德指数（Rand index，RI）基本思想是假设k个批次数据中共有n个样品，用某种聚类算法将样品分成k类，计算批次和聚类中样品配对组合完全一致的数目n11与完全不一致的数目n00之和与样品中随机配对组合数的比值［21］，即

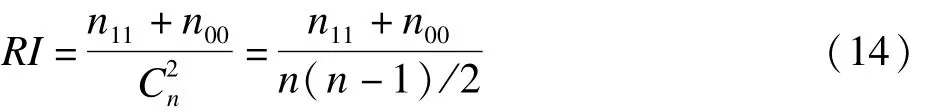
当样品随机分配到聚类的组别中，RI取值接近0。但是，当批次与样品是相同数量级排序时，RI无法为0。为此，可以使用校正兰德指数（CRI），即

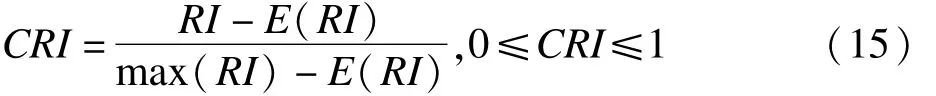
E（RI）和max（RI）有专门的计算公式。当对象随机分配到聚类的组别中，CRI取值接近0，即批次和聚类结果无关。

（2）信息变异

信息变异（VI）与互信息概念有关。假设有n个样品的 k个批次 A＝｛A1，A2，…，Ak｝，聚类为 k个组别B＝｛B1，B2，…，Bk｝，则 VI指标用下式计算，即

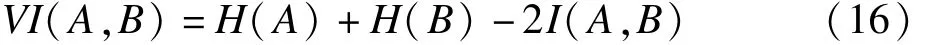
其中H（·）为熵，I（·，·）是两种分类（批次和聚类结果）的互信息，0≤VI（A，B）≤min（log（n），2log（k）），VI＝0表示两个批次完全分开，实际中越大越好。

结 语

基因组学数据的快速增长为肿瘤生物学、寻找生物标志物及药物治疗靶点提供了更好的研究基础。尽管研究者需要面对批次效应的问题，但近年数据整合算法已经有了实质性的发展，从而能够为我们提供更可靠的统计处理结果。Jason Rudy和FaramarzValafar的研究表明，EB、XPN和DWD在对数转化的基因组学微阵列数据中表现最好，PLIDA则要求表达值在线性范围内变化。在样本量方面，EB算法可用于单批次小样本的基因组学数据（检测的n＜10），而其他算法通常要求单批次样本量n≥25。可以预测，今后在不同平台或批次检测的数据整合技术上会有进一步的发展。

［1］Golub TR，Slonim DK，Tamayo P，et al.Molecular classification of cancer:class discovery and class prediction by gene expression monitoring.Science，1999，286（5439）:531-537.

［2］Bittner M，Meltzer P，Chen Y，et al.Molecular classification of cutaneous malignant melanoma by gene expression profiling.Nature，2000，406（6795）:536-540.

［3］Tinker AV，Boussioutas A，Bow tell DD.The challenges of gene expression m icroarrays for the study of human cancer.Cancer Cell，2006，9（5）:333-339.

［4］Scherer A.Variation，Variability，Batches and Bias in Microarray Experiments:An Introduction.John Wiley＆Sons，Ltd，2009:1-4.

［5］Luo J，Schumacher M，Scherer A，et al.A comparison of batch effect removal methods for enhancement of prediction performance using MAQC-II microarray gene expression data.Pharmacogenomics J，2010，10（4）:278-291.

［6］Leek JT，Scharpf RB，Bravo HC，et al.Tackling the w idespread and critical impact of batch effects in high-throughput data.Nat Rev Genet，2010，11（10）:733-739.

［7］Rudy J，Valafar F.Empirical comparison of cross-platform normalization methods for gene expression data.BMC Bioinformatics，2011，12:467.

［8］Chen C，Grennan K，Badner J，et al.Removing batch effects in analysis of expression microarray data:an evaluation of six batch adjustment methods.PLoSOne，2011，6（2）:e17238.

［9］Johnson WE，Li C，Rabinovic A.Adjusting batch effects in microarray expression data using empirical Bayes methods.Biostatistics，2007，8（1）:118-127.

［10］Stein CK，Qu P，Epstein J，et al.Removing batch effects from purified plasma cell gene expression microarrays with modified Com Bat.BMC Bioinformatics，2015，16（1）:63.

［11］Shabalin AA，Tjelmel and H，Fan C，et al.Merging two gene-expression studies via cross-platform normalization.Bioinformatics，2008，24（9）:1154-1160.

［12］Deshwar AG，Morris Q.PLIDA:cross-platform gene expression normalization using perturbed topic models.Bioinformatics，2014，30（7）:956-961.

［13］Heinrich G.Parameter estimation for text analysis.Technical Report，2004.

［14］Sims AH，Smethurst GJ，Hey Y，et al.The removal of multiplicative，systematic bias allows integration of breast cancer gene expression datasets-improving meta-analysis and prediction of prognosis.BMC Med Genomics，2008，1:42.

［15］Li C，Wong WH.Model-based analysis of oligonucleotide arrays:expression index computation and outlier detection.Proc Natl Acad Sci USA，2001，98（1）:31-36.

［16］Jiang H，Deng Y，Chen HS，et al.Joint analysis of two m icroarray gene-expression data sets to select lung adenocarcinoma marker genes.BMC Bioinformatics，2004，5:81.

［17］Lazar C，Meganck S，Taminau J，et al.Batch effect removal methods form icroarray gene expression data integration:a survey.Brief Bioinform，2013，14（4）:469-490.

［18］Gagnon-Bartsch JA，Speed TP.Using control genes to correct for unwanted variation in microarray data.Biostatistics，2012，13（3）:539-552.

［19］Kim KY，Kim SH，Ki DH，et al.An attempt for combining microarray data sets by adjusting gene expressions.Cancer Res Treat，2007，39（2）:74-81.

［20］Vaisipour S.Detecting，correcting，and preventing the batch effects in multi-site data，with a focus on gene expression Microarrays.University of Alberta，2014.

［21］Vinh NX，Epps J，Bailey J.Information Theoretic Measures for Clusterings Comparison:Is a Correction for Chance Necessary？Proceedings of the 26th International Conference on Machine Learning（ICML-09），2009.

国家自然科学基金资助（81473072）

（责任编辑:郭海强）