高维组学数据的变量筛选方法及其应用*

侯 艳 谢宏宇 张晓凤 李 康△

·方法介绍·

高维组学数据的变量筛选方法及其应用*

侯 艳1，2谢宏宇1张晓凤1李 康1△

随着生物检测技术的不断发展，实际中可以获得基因组、蛋白质组和代谢组等各种来源的高维组学数据，如何从海量数据中准确选择与疾病有关的特征变量，从而构建准确的预测模型一直是国内外的研究热点。变量筛选问题可归结为从一组检测数据Χ＝（Χ1，Χ2，…，Χm）中筛选出对分类/预测有区分作用的“最优”子集Χsub。目前高维组学变量筛选方法主要有传统的统计学方法和机器学习方法，前者主要分为参数和非参数方法两类，这部分主要是基于概率分布的统计推断；后者主要包括有监督学习（supervised learning）和无监督学习（unsupervised learning）算法，其主要差别为在训练集中是否用到分组信息。本文主要针对常见的单变量筛选方法和多变量有监督学习的变量筛选方法做一介绍。

过滤式变量筛选方法

过滤式变量筛选方法（filtermethods）是指通过观察到的原始数据，计算变量与疾病之间的相关性指标（如t值，P值等），并通过设定阈值选择特征变量，去除相关性较弱或组间差异不大的变量，从而直接得出与疾病具有一定关联性的特征变量的一类方法。由于这类筛选方法独立于判别模型（分类器），因此通过这类方法选择出来的特征变量可以用于评价不同判别（预测）模型的效果。过滤式方法的优点是计算简单、能够快速地降维，并且不依赖特定的判别模型；缺点主要是忽略了特征变量之间可能存在的相关关系，因此在与其他类型变量选择方法相比较时，分类效果并不理想。同时变量筛选的结果很大程度上受到阈值影响，如何确定阈值也是需要考虑的问题之一［1］。

1.单变量过滤方法

单变量过滤方法由于其计算简单直接，而成为目前较为常用的一类变量筛选方法。常用的单变量过滤式筛选方法包括Satterthwaite近似t检验、Wilcoxon秩和检验、ROC曲线下面积、置换检验（permutation test）、互信息（mutual information）、welch t检验、χ2检验、SAM（significance analysis of microarrays）、SAMROC（significance analysis of ROC indices）等［2］，其中χ2检验主要用于结构基因组的 SNP分析［3］，SAM和SAMROC方法主要用于基因表达数据分析［4］，其他方法则可以应用于各种组学数据的特征变量筛选。

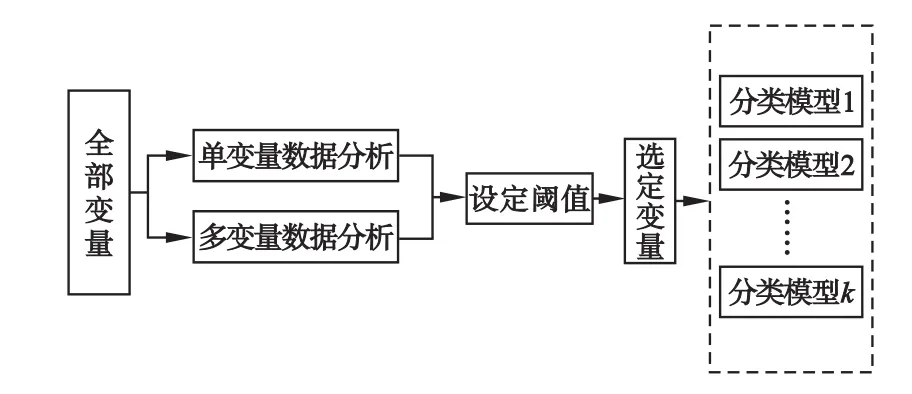
图1 过滤式变量筛选方法过程

SAM法的基本原理是在传统t检验公式的分母中加上一个较小的正数s0（取值通过样本数据计算），从而避免将表达水平和变异程度均较低的无生物学意义的基因识别为差异表达基因［5］。SAMROC方法则是按照另一种原则计算SAM法中的修正参数s0，其基本思想是选择一个合适的s0，使筛选出的“差异基因”能够保证具有最小的假阳性率和假阴性率［6］。置换检验则是通过不断打乱分类标签，形成原假设的分布，在此基础上进行检验。以上方法均首先需要对变量的重要性排序，在此基础上通过选择合适的阈值给出筛选的结果。实际上，阈值的选择主要根据检验的P值确定，例如Bonferroni校正P值或FDR（false discovery rate）。在高维组学数据中，Bonferroni校正 P值的方法筛选变量过于严格，因此更多使用的是FDR校正后的P值，其代表该变量为假阳性的概率估计值。需要注意的是，使用FDR校正后的P值需要基于变量间独立的假设，而实际数据常常并不能满足这一条件，因此得到的P值是一个“近似值”［7］。

2.多变量过滤方法

由于单变量过滤方法假定变量间相互独立，并没有考虑到变量之间的相互关系，因此提出了多变量过滤方法，意在去除信息重叠的自变量以及筛选具有简单交互作用的变量。

（1）基于关联的特征选择方法

基于关联的特征选择方法（correlation-based feature selection，CFS）是一种基于相关性实现变量筛选的方法，主要思想是通过计算各子集中每个变量与类别的关联度及变量之间的冗余度来实现最终变量的筛选过程，其中关联度越大、冗余度越小则效果越高［8］。在CFS算法中，利用信息增量计算变量之间的关联大小，根据基于相关性的启发式评价函数max｛H（Rij）｝选择变量组合，其中Rij为所有变量的关联矩阵。评价函数的特点是自变量与因变量高度相关，而自变量之间尽量不相关。

（2）基于马尔科夫毯的特征变量筛选方法

马尔科夫毯（Markov blanket）是指在一个网络中，目标结点的父结点、子结点和配偶结点。实际中可以把标签变量作为目标结点，通过寻找其马尔科夫毯屏蔽网络中其他变量对该变量的影响，即选择与标签变量具有直接关系的变量［9］。贝叶斯网络，给定了目标变量的马尔科夫毯，就可以求出该变量的条件概率分布，网络中的其他变量就可以看作是冗余的，因此寻找目标变量的马尔科夫毯实质就是变量筛选的过程。目前常用的基于马尔科夫毯的变量筛选方法，主要包括基于回归分析的马尔科夫毯学习算法和基于贝叶斯网络的马尔科夫毯学习算法［10－11］。

（3）Boost方法

这是专门用于GWAS数据分析两变量交互作用的一种方法，其基本思想是通过使用两个对数线性模型，即含交互作用项的饱和模型与不含交互作用项的关联模型似然值之差，得到两个位点的交互作用［12］。这种算法的核心是使用了一种被称为KSA的算法，可以替代极大似然估计来计算两变量不同水平组合概率的估计值。由于KSA不需要迭代过程，从而能够在短时间内快速穷举所有的SNP交互组合。但是使用这种方法只能筛选具有一阶交互作用的变量，并且只适合离散变量交互作用的筛选。

除上述方法外，还有最小冗余-最大相关（minimum redundancy-maximum relevance，MRMR）［13－14］和不相关缩减重心（uncorrelated shrunken centroid，USC）算法［15］等其他方法。

封装式特征筛选方法

封装法（wrappermethod）是从所有变量组合中尽量选择“最优”变量组合，它将变量的选择看作是一个搜索寻优的问题，即根据一定的算法和目标函数给出“最优”的变量组合［16］。封装法与过滤法变量选择的不同在于变量选择过程中是否引入了分类模型和算法。通常其评价函数以优化分类准确性为目的（图2）。因此，这种方法实际就是把分类或预测与变量筛选封装到一起，每次评价一个变量组合。封装式方法的优点主要表现在将变量组合的搜寻与分类模型的选择结合在一起，既考虑到了模型内变量间的相关关系，同时又不受模型外部无关变量的影响。封装法选择“最优”变量组合通常采用的策略是启发式搜索，即利用启发函数随时调整搜索的先后顺序，具体包括确定性和随机性两种搜索策略。这种方法的缺点表现在与过滤式方法相比有更高的过拟合风险，由于需要不断迭代搜索使计算量明显增大［17］。

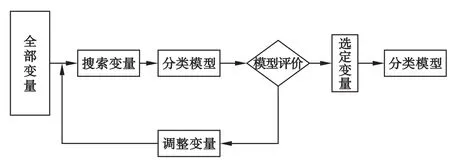
图2 基于封装式的变量筛选过程

1.确定性搜索算法

确定性搜索算法是指在确定的初始状态下，利用一定的规则使问题得到全局或者局部最优解，其中主要有全局最优搜索和序列搜索两种算法，这种方法的特点是得到的结果完全确定。由于全局最优搜索算法需要在2m－1（m为变量的数目）种组合中寻优，极为耗时，因此实际中使用最多的是序列搜索方法，即按照一种规则，不断将问题简化为一个规模更小的类似子集问题，直接达到最终状态。

（1）序列前进选择法

序列前进筛选法（sequential forward selection，SFS）是将变量逐步加入模型。初始状态可以是单变量分析中最显著的变量，每次都计算评价函数以决定是否加入一个新的变量。例如可以使用模型前后两次的预测效果变化作为评价函数，预测能力的计算可以使用交叉验证的方法进行评价。这种方法的主要缺点是对于进入模型变量的评价未充分考虑变量的组合作用［18］。

（2）序列后退剔除法

序列后退剔除法（sequential selection elimination，SSE）可以克服序列前进方法的缺点。这种方法的初始状态是纳入全部变量，每次计算评价函数决定是否剔除模型中的一个变量。相比之下，这种方法能够更充分考虑变量间的组合作用，因此更为合理，也是目前使用比较多的一种方法。这种方法的主要问题是，在高维数据情况下，计算量比较大，例如有2万个变量，需要拟合约2万个模型，如采用5折交叉验证，则需要拟合10万个模型。

（3）序列浮动选择法

序列浮动选择法（sequential floating selection）与前面两种方法不同的是，在计算过程中变量并非逐个进入或者剔除，而是以变量的子集形式进入模型，在选择方法方面可以采用前进和后退两种方式。例如可以通过对变量先行排序，然后使用0.618黄金分割比例的方法，选择一定数量的变量组合拟合模型，并与之前的模型进行比较，通过比较决定下一步分割的方向，在这个过程中，退出和进入模型的变量数目可以不断变化［19］。

需要注意:三种序列选择方法都属于贪心算法，即在对问题求解时，做出在当前看来是最好的选择，导致筛选出的变量可能是局部最优。

2.随机性搜索算法

随机算法是利用概率机制而非确定性的点描述迭代过程。随机性封装算法的优点是可以避免局部最优，可与分类器结合进行筛选；缺点是计算量大，变量选择依赖于分类器，与确定性学习算法相比具有更高的过拟合风险。目前，随机性搜索方法主要有模拟退火算法（simulated annealing）［20］、遗传算法（genetic algorithm）［21－22］和免疫遗传算法（immune genetic algorithm，IGA）［23］等。

（1）模拟退火算法

模拟退火算法是基于蒙特卡洛（Monte-Carlo）迭代求解的一种随机寻优算法，其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性，即从某一较高初温（粒子无序状态）出发，随温度参数的不断下降，结合粒子趋于平衡的变化概率，随机寻找目标函数的全局最优解。这种算法的本质是在贪心搜索算法的基础上引入随机因素，即以一定的概率来接受一个比当前解要好的解，因此可以有效地避免局部的最优解。这种方法的主要问题是温度管理（计算过程）参数难以控制。

（2）遗传算法

遗传算法（GA）是一种模拟生物的进化过程而提出的启发式搜索方法，即通过模拟生物界“适者生存”的遗传进化策略，不断对染色体上的基因（变量）进行筛选和重组，实现对高维数据进行“最优”变量组合的搜索。遗传算法的特点是采用简单编码技术表示复杂结构，并通对编码的遗传操作（复制、交叉和变异）产生备选的变量组合解，通过优胜劣汰的选择机制进行导向性搜索。遗传算法的主要优点:能够回避局部解的问题，对变量的数目无限制，可以在大范围内进行搜索；主要问题表现为GA存在模式收敛性质，由于局部强势的染色体（变量组合）不断复制，难以维持模式的多样性，容易出现“早熟”或者“退化”的现象，影响变量筛选的优化结果。

（3）免疫遗传算法

免疫遗传算法是将免疫算法和遗传算法的优点结合起来的优化算法。为了使遗传算法在染色体（变量组合）多样化和群体收敛之间取得平衡，并克服遗传算法的缺点，在遗传算法中加入了免疫的思想，即在遗传算法中加入免疫算子，使遗传算法变成具有免疫功能的新算法。免疫算子在实现快速优化的同时，通过不断调节抗体（备选的变量组合）浓度维持多种抗体的并存（变量组合的多样性），从而能够根据抗原（需要解决的问题）给出“最优”的变量组合结果。抗体浓度需要根据抗原-抗体、抗体-抗体的亲和力计算，抗原-抗体亲和力评价实际就是目标函数值，抗体-抗体的亲和力评价为抗体之间的相似度。这种算法的主要任务是设定特定的增强群体多样性的免疫算子与遗传算法相结合，避免出现“早熟”或者“退化”的现象。基于抗体浓度的群体更新、保持模式多样性是免疫算法的重要任务，也是这种算法的重要特征。另外，这种方法更适合多目标的变量筛选。

嵌入式变量筛选方法

嵌入式变量筛选方法（embedded method）是针对特定的模型和算法，筛选出对模型有重要意义的变量组合，即在建立模型的同时，可以给出各变量重要性的得分值，从而用于分类或预测［17］（图3）。这种方法可以通过结合不同分类算法来改善整体预测准确性，主要有偏最小二乘回归（partial least squares regression，PLSR）［24］、支 持 向 量 机 （support vector machine，SVM）［25］、随机森林（random forest，RF）［26］和惩罚回归（penalized regression）［27］等方法。嵌入式变量筛选方法的特点是，变量筛选通常只需要拟合一个模型，与封装式变量筛选相比需要的计算量更小。

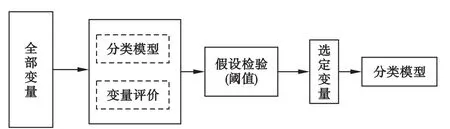
图3 基于嵌入式的变量筛选方法过程

1.偏最小二乘回归

偏最小二乘回归（PLSR）是一种将主成分分析和回归分析结合在一起的方法［24］。这种方法与主成分回归十分相似，即在自变量信息不变的条件下对其进行主成分提取，但需要同时保证主成分提取时自变量的主成分与因变量之间的相关性最大化，在此基础上间接拟合自变量与因变量数据之间的线性关系:

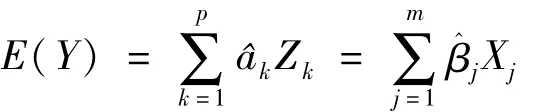
这里，E（Y）表示因变量Y的期望值，Zk为选定的PLS主成分，m为变量的个数，p（p＝1，2，…，m）为所取的PLS成分数，为可视化通常取p≤3。变量筛选的依据是计算各变量的投影重要性评分统计量:

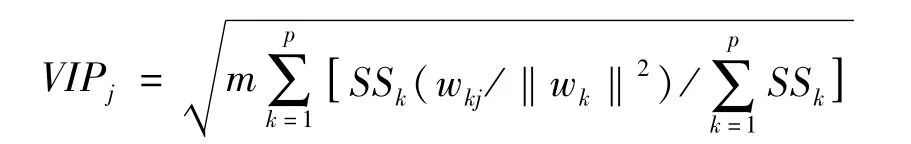
其中SSk为第k个PLS主成分的平方和，wkj为自变量Xj（j＝1，2，…，m）在第 k个主成分上载荷系数，说明该自变量在第k个PLS成分中对因变量Y的影响，Y∈｛－1，1｝，wk＝（wk1，wk2，…，wkm）。

上式中的VIPj反映了某个自变量对于因变量和整个模型的贡献大小。Wold建议，如果VIPj＞0.8则认为变量的贡献较大，实际中通常取VIPj≥1作为选择变量的阈值。这一指标的主要缺点是其值大小是相对的，只能说明哪些自变量的作用更大一些，因此也有学者建议同时考虑回归系数估计值和VIP值大小来进行变量筛选。

需要注意:PLSR方法同样可以用作过滤式和封装式变量筛选。究竟属于哪种方法，关键是看其是否最后要用PLSR作为分类模型和是否具有迭代过程，如果主要目的仅是作为变量初筛选，则属于过滤法；如果在变量组合寻优的过程中使用PLSR模型作为分类评价的标准，则属于封装式变量筛选方法。

2.支持向量机

支持向量机（SVM）是一种非常有效的分类模型或机器学习方法［25］。这种方法首先构造一个线性判别函数 g（X）:

其中，X＝（X1，X2，…，Xm），φ（X）＝｛φ1（X），φ2（X），…，φd（X）｝T表示采用线性或非线性变换的方法将X映射到另一特征空间（通常d＞m），wj是需要估计的权重系数，W＝（w1，w2，…，wd）T，b0是与判别阈值有关的一个常量。对于每个样品 Xi（i＝1，2，…，n）都属于两类中的一类，相应的标记为yi＝±1。

为了能够实际应用，在新的特征空间φ（X）中寻找能将类别很好分开的两个平行的标准超平面，并使其间隔最大，落在标准超平面上的数据点称作支持向量，此时，式中 SV是所有的支持向量，αj是满足一定条件并且符号为正的系数。将样品数据代入下式，根据得出的符号即可完成对样品的分类:

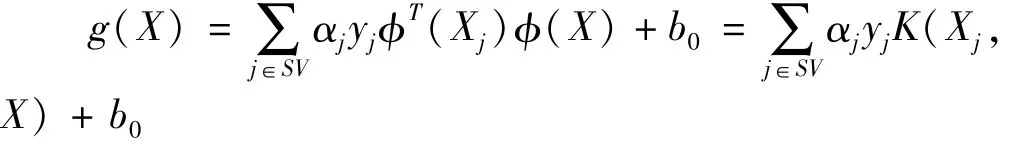
其中K（Xj，X）为核函数。由此看到，这里将变换后空间向量的内积表示为原始变量空间对应向量的内积函数，即不需要明确知道φ的具体形式，而是通过计算核函数K（Xj，X）的值来计算内积。SVM筛选变量的思想是，在选择线性核函数情况下，根据SVM的权重向量确定各变量对于判别模型的重要程度。

需要注意的是，在高维情况下直接使用SVM嵌入式变量筛选方法，很难获得理想的结果，通常需要结合封装式算法。例如目前使用比较多的SVM-RFE使用的就是序列后退剔除法。

3.随机森林

随机森林（random forest，RF）是一种基于分类树算法的组合分类模型［26］。RF的基本思想是，通过自助法（bootstrap）重抽样技术从原始数据中有放回地随机抽取Ntree个自助样本，对每个样本都建立一个二元递归分类树。按照这种做法，每个自助样本平均不包含37%的原始数据，将这些数据称为袋外数据（OOB数据），并作为RF的测试样本；最后，由训练样本生成b个分类树组成随机森林，根据分类树投票形成的分数确定测试数据的分类结果。RF具有很高的预测准确率，对异常值和噪声有很强的容忍度，能够处理高维数据（变量个数远大于观测个数），有效地分析非线性和交互作用的数据，并能够在建立RF模型的同时给出变量重要性评分（variable importance measures，VIM）。变量的筛选可以依据不同的统计量和筛选过程，各变量 Xj（j＝1，2，…，m）VIMj值的计算方法有多种，但都是通过比较原始变量值和随机打乱变量值后对RF预测的影响进行估计，两者差别越大说明该变量越重要，VIMj值越大。

4.bagging方法

bagging是英文 bootstrap aggregating的缩写，该学习算法可以进行多轮预测，每轮的训练集由从初始的样本中重复抽取一定数量的训练样本，从而得到对应的预测函数，最终的预测函数为多轮预测函数分类结果的综合投票或计算平均值进行排序，从而确定特征变量的重要性。例如变量捕获（variable hunting）方法使用的就是bagging策略，其基本思想是利用重抽样方法不断抽取一定比例的样本，同时在所有变量中抽取一定数量的变量进行建模，然后利用检验统计量的概率分布确定阈值，在此基础上进行变量筛选。上述过程重复多次，计算平均筛选变量的个数，再根据各变量被筛选出来的频率进行排序，选择排列在前面的变量作为最终筛选出的重要变量。改变筛选变量过程的不同参数，可以获得不同数量的“差异变量”。这里，用于筛选变量的预测模型可以使用任何一种基础分类模型（如PLSR、SVM和RF等）。理论上，这种方法可以应用于任意高维变量的组学数据中，筛选变量的稳定性非常好，而且使用其筛选出的变量进行预测效果较优，拓宽了各种分类模型的应用范围［27］。

5.boosting方法

boosting方法是一种基于一系列弱基础分类器的组合分类模型，这种方法需要不断在内部进行迭代，在训练开始时先为每一个样品赋予一个相等的权值，接下来进行N次迭代训练。每次训练中，根据每个样品现有的权重，寻找一个最优分类模型，如果此分类模型导致样品被错分，则根据错分的情况重新计算样品的权重，即在下次迭代中为其赋予更大的权重值。N次训练结束，每个单独的分类模型亦根据其对样本的预测效果，赋予不同权重，预测效果越好，给予的权重越大，最后将所有分类模型组合在一起。因此，这种算法使用的是一系列反映数据不同方面的加权分类模型，最终产生一个分类准确度更高的组合分类模型。变量筛选则可以通过对单个基础分类模型中变量重要性得分进行平均实现。理论上，这种方法能够获得最优的变量筛选和预测结果。

6.正则化回归方法

正则化（regularization）是指对最小化经验误差函数加约束，即对其附加先验知识。典型的两种正则化回归是岭回归（ridge regression）和 lasso回归［28］。两种方法都是针对多元线性模型的问题提出的，岭回归是在最小化残差平方和上加一个正则化的L2范数项λ‖β收缩惩罚项，即对如下损失函数极小化:

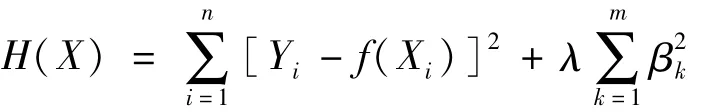
通过使残差平方和最小化的原则，求出各变量的回归系数。使用岭回归主要解决自变量的共线问题。lasso回归则对回归系数进行了L1惩罚，即加入L1范数项

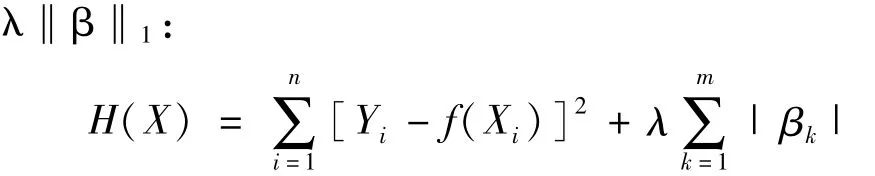
lasso回归主要解决变量筛选问题，通过调整正则化参数λ，能够自动将与分类无关变量的回归系数置接近于0，实现变量的自动筛选。

从统计学角度，使用L2范数不仅可以避免共线以及在变量数目大于样本量时出现病态矩阵求逆的问题，同时能够避免模型过拟合、防止算法陷入局部最小化，提高模型的外部预测能力。使用L1范数的好处是可以自动实现变量选择，同时保证模型具有可解释性。正因如此，目前已根据这一原理提出了使用L1＋L2惩罚建立的各种算法，如弹性网算法、分组lasso算法、稀疏分组lasso算法等，以适应更复杂的多组学高维数据分析。同理，上述原理也适用于logistic模型、偏最小二乘回归（PLSR）和支持向量机（SVM）等模型。

总结和展望

本文对目前高维组学变量筛选的方法做了简单的描述和评述。基于变量选择的方式可以分成三类:过滤式方法、封装式方法和嵌入式方法。过滤式方法是简单地根据重要性原则将变量排序，同时按照阈值来选择特征变量。过滤式方法的主要缺点:为了选择变量子集需要设定阈值，因此变量筛选依赖阈值，并且没有适合的交叉验证调整方法，很难得出较为可靠的结果。使用交叉验证方法能够快速选择阈值，将过滤式方法转变为封装式方法，这种方法将变量选择封装在模型中；为了提高模型的解释性，筛选有意义的变量，这些方法需要反复对模型的预测准确性进行评价。封装式方法的主要问题是计算量大，并且需要调整大量复杂的参数。嵌入式方法以一种很好的结构形式进行变量筛选，将变量筛选与建模整合在一起。然而，很多的嵌入式方法通过内部交叉验证选择变量，这不可避免地在一定程度上减慢了计算的速度。

目前，很多研究者试图比较各种变量选择方法，通常是为了表明新的方法性能的提高，并未对大范围的数据集进行客观的比较，给出最终的参考意见。因为方法和数据性质之间存在相互作用，在实际中，并没有一种适合所有数据的最优变量选择方法。通过本文的综述，希望读者更好地了解文献中报道方法之间的相似性和不同，能够根据实际需要进行选择。

本文观点，有三种方法特别值得关注，即bagging、boosting和正则化方法。前两种方法属于组合分类器方法，主要是算法问题。bagging方法的特点是对数据的维数完全没有限制（如m＞300000），筛选变量的结果较其他方法更为稳定；boosting方法在针对生物异质性和亚组分析时，更显现出其作用。正则化方法则在理论上相对更为完善，使用灵活，根据研究目的通过调整惩罚项和正则参数选择合适的变量，其最大的特点是对变量的维数没有限制，模型结构性强、具有可解释性。更深入地，上述三种方法结合调控网络与生物实质问题相融合，有待进一步发展。

［1］Hira ZM，Gillies DF.A Review of Feature Selection and Feature Extraction Methods Applied on M icroarray Data.Advances in bioinformatics，2015，2015:198363.

［2］Saeys Y，Inza I，Larranaga P.A review of feature selection techniques in bioinformatics.Bioinformatics，2007，23（19）:2507-2517.

［3］Bo TH，Jonassen I.New feature subset selection procedures for classification of expression profiles.Genome Biol，2002，3（4）:RESEARCH0017.

［4］Liu XX，Krishnan A，Mondry A.An Entropy-based gene selection method for cancer classification usingm icroarray data.BMC bioinformatics，2005；6:76.

［5］Tusher VG，TibshiraniR，Chu G.Significance analysis ofm icroarrays applied to the ionizing radiation response.Proceedings of the National Academy of Sciences of the United States of America，2001，98（9）:5116-5121.

［6］Tsai CA，Chen JJ.Significance analysis of ROC indices for comparing diagnosticmarkers:applications to genemicroarray data.Journal of biopharmaceutical statistics，2004，14（4）:985-1003.

［7］Hong WJ，Tibshirani R，Chu G.Local false discovery rate facilitates comparison of different m icroarray experiments.Nucleic acids research，2009，37（22）:7483-7497.

［8］Ooi CH，Chetty M，Teng SW.Differential prioritization between relevance and redundancy in correlation-based feature selection techniques for multiclass gene expression data.BMC bioinformatics，2006，7:320.

［9］Tan Y，Liu ZF.Feature selection and prediction with a Markov blanketstructure learning algorithm.BMC bioinformatics，2013，14（Suppl 17）:A3

［10］Borchani H，Bielza C，Martinez-Martin P，et al.Markov blanketbased approach for learningmulti-dimensional Bayesian network classifiers:An application to predict the European Quality of Life-5 Dimensions（EQ-5D）from the 39-item Parkinson′s Disease Questionnaire（PDQ-39）.Journal of biomedical informatics，2012，45（6）:1175-1184.

［11］Bui AT，Jun CH.Learning Bayesian network structure using Markov blanket decomposition.Pattern Recogn Lett，2012，33（16）:2134-2140.

［12］Xu M，Zhang AD.Boost feature subset selection:A new gene selection algorithm for m icroarray dataset.Lect Notes Comput Sc，2006，3992:670-677.

［13］Sakar CO，Kursun O，Gurgen F.A feature selection method based on kernel canonical correlation analysis and the m inimum Redundancy-Maximum Relevance filtermethod.Expert Syst Appl，2012，39:3432-3427.

［14］Peng HC，Ding C，Long FH.M inimum redundancy-Maximum relevance feature selection.Ieee Intell Syst，2005，20:70-71.

［15］Christin C，Hoefsloot HC，Sm ilde AK，et al.A critical assessment of feature selection methods for biomarker discovery in clinical proteom ics.Molecular＆cellular proteom ics:MCP，2013，12（1）:263-276.

［16］Liu B，Cui Q，Jiang T，et al.A combinational feature selection and ensemble neural networkmethod for classification of gene expression data.BMC bioinformatics，2004，5:136.

［17］Semmar N，Canlet C，Delplanque B，et al.Review and research on feature selectionmethods from NMR data in biological fluids.Presentation of an originalensemblemethod applied to atherosclerosis field.Current drug metabolism，2014，15（5）:544-556.

［18］Hatamikia S，Maghooli K，Nasrabadi AM.The emotion recognition system based on autoregressive model and sequential forward feature selection of electroencephalogram signals.Journal of medical signals and sensors，2014，4（3）:194-201.

［19］Reneker J，Shyu CR.Applying sequential forward floating selection to protein structure prediction with a study of HIV-1 PR.AM IA Annual Symposium proceedings/AM IA Symposium AM IA Symposium，2006:1072.

［20］Ghosh P，Bagchi MC.QSAR modeling for quinoxaline derivatives using genetic algorithm and simulated annealing based feature selection.Current medicinal chem istry，2009，16（3）:4032-4048.

［21］Cho HW，Kim SB，Jeong MK，et al.Genetic algorithm-based feature selection in high-resolution NMR spectra.Expert Syst Appl，2008，35（3）:967-975.

［22］Sahiner B，Chan HP，WeiD，etal.Image feature selection by a genetic algorithm:application to classification of mass and normal breast tissue.Medical physics，1996，23（10）:1671-1684.

［23］Luo JW，Wang T.Motif discovery using an immune genetic algorithm.Journal of theoretical biology，2010，64（2）:319-325.

［24］Lee D，Lee Y，Paw itan Y，etal.Sparse partial least-squares regression for high-throughput survival data analysis.Statistics in medicine，2013，32（30）:5340-5352.

［25］Jiang Z，Yamauchi K，Yoshioka K，et al.Support vector machinebased feature selection for classification of liver fibrosis grade in chronic hepatitis C.Journal of medical systems，2006，30（5）:389-394.

［26］Saraswat M，Arya KV.Feature selection and classification of leukocytes using random forest.Medical＆biological engineering＆computing，2014，52（12）:1041-1052.

［27］Dettling M.Bag Boosting for tumor classification with gene expression data.Bioinformatics，2004，20（18）:3583-93.

［28］Breheny P，Huang J.Coordinate Descent Algorithms for Nonconvex Penalized Regression，with Applications To Biological Feature Selection.The annals of applied statistics，2011，5（1）:232-253.

国家自然科学基金资助（81573256，81473072），中国博士后基金面上项目（2015M 571445）

1.哈尔滨医科大学卫生统计学教研室（150081）

2.心血管医学研究教育部重点实验室（哈尔滨医科大学）

△通信作者:李康，E-mail:likang@ems.hrbmu.edu.cn

（责任编辑:郭海强）