区间删失生存数据的统计分析方法及其应用*

李丽贤 汤 茗 曾彦彦 沈罗英 李钊洪 陈慧林 郭胜楠 陈金宝 侯雅文 陈 征△

区间删失生存数据的统计分析方法及其应用*

李丽贤1＃汤 茗1＃曾彦彦1沈罗英1李钊洪1陈慧林1郭胜楠1陈金宝1侯雅文2陈 征1△

在临床研究中，当只知道事件发生在某一给定的时间区间内，而不知道其确切时间点时，将这类数据称为区间删失数据（interval censored data），表示为T∈（L，R］［1］，其中 T表示个体的生存时间，L表示删失区间的下界，R表示上界。显而易见，区间删失包括左删失和右删失，临床研究中，区间删失现象比较常见，特别是在患者进行周期性随访的临床试验和队列研究中。

在处理区间删失数据时，很多研究者往往为简便起见，直接用删失区间的中点或右端点作为生存时间的估计值，再利用类似于处理“右删失资料”的方法估计生存率，并据此进行参数估计和假设检验［2］。Dorey［3］等通过模拟研究发现，若将删失区间的中点作为观察时间，用右删失方法处理，则会高估生存率。此外，Rücker［4］等发现，若将删失区间的右端点作为观察时间，进行Kaplan-Meier估计，则会过低估计误差方差，从而易得出假阳性的结果。可见，这些简单的处理方式不仅会降低生存率估计的准确性，而且会影响估计的精度，是不合理的。因此，采用专门的统计分析方法来处理区间删失数据是非常必要的。本文将介绍有关区间删失数据的非参数方法以及半参数模型，并以“静脉注射毒品成瘾患者的HIV感染情况的生存分析”为例，展示其应用。

原理与方法

1.非参数估计

设第 i个个体的生存时间为 Ti（i＝1，…，n），（Li，Ri］为 Ti所属的删失区间，S（t）＝P（T＞t）为生存函数（即生存率）。令｛τj（即｛0＝τ0＜τ1＜τ2＜…＜τj＜…＜τm｝）等于｛0，Li，Ri；i＝1，…，n｝为唯一顺序元素，可见｛τj为研究中能观察到的全部时间点（也就是所有观察区间的端点），τj为第j＋1个时间点。使 αij＝I（（τj－1，τj］∈（Li，Ri］），i＝1，…，n，j＝1，…，m，I（）为指示变量，对于第 i个个体，若区间（τj－1，τj］包含在区间（Li，Ri］中，则 αij＝1，否则为 0，由 αij可得知，一个发生在区间（Li，Ri］上的事件，是否发生在（τj－1，τj］上。定义 pj＝S（τj－1）－S（τj），j＝1，…，m，p＝（p1，…，pj，…，pm）T，pj在这里表示第 j个时间点的死亡概率。似然函数可表示为

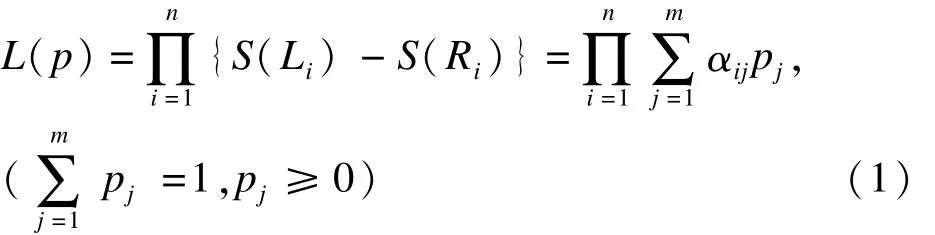
取对数，得对数似然函数 log（L（p）），然后对 pj求偏导数有

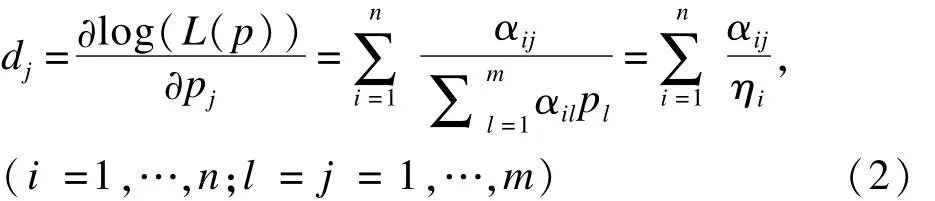
这里，ηi表示第 i个个体的死亡概率，dj则为在（τj－1，τj］区间上的所有个体的ηi倒数之和。

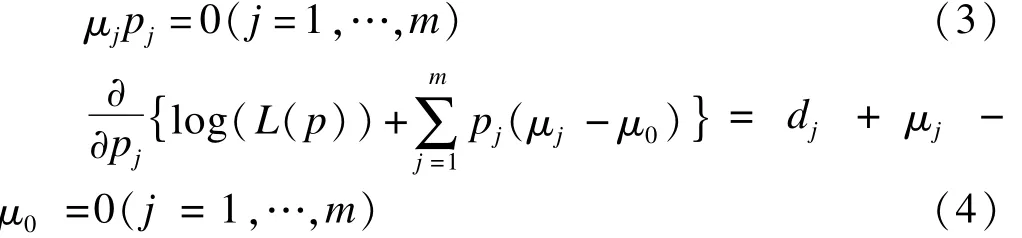
由公式（3）和（4），可知当 pj＞0时，μj＝0，dj＝μ0＝n，而当 pj＝0时，μj≥0，dj＝μ0－μj≤n。当 μj≥0和 dj＋μj－μ0＝0称之为满足库恩-塔克条件。因此，对所有的 j，当 dj＝n（j＝1，…，m）时，p为所求的 NPMLE。值得注意的是，Peto［7］提出:只有当 τj－1＝Li和 τj＝Rk（i≠k）时［7］，有 pj≥0，但不排除满足以上两个条件后，仍有一些pj＝0。

求S（t）和p的过程中，可通过不同的迭代计算方法进行求解。其中，Turnbull［8］提出的修正乘积极限估计算法（Turnbull算法），以及 Gentleman［9］在 EM算法的基础上提出的修正EM算法应用较为广泛。

（1）Turnbull算法

Turnbull［8］提出了一种类似乘积极限估计的方法，该生存函数估计式可以由自一致性算法来估计。迭代的初始值由乘积极限法求得，设为的第r次迭代结果，其迭代过程可表示为:

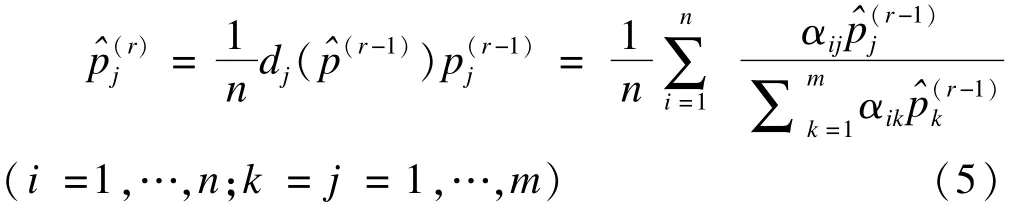
（2）EM修正算法

修正EM算法为Gentleman和Geyer在EM算法的基础上提出的一种修正迭代算法［1］，初始值的极大似然估计的计算分为两个部分——降维与最优化。计算出初始值后，使用EM算法对其进行迭代，计算出新的生存函数估计式与该区间内的死亡概率。当某些区间的死亡概率低于某个值的时候，先将区间的死亡概率归为0，并验证库恩-塔克条件，即验证此区间的死亡概率是否真正为0。若不满足，则将区间内的概率密度函数加上一较小值，再进行EM算法迭代。当迭代之后最大的变化量小于某个规定值，并且满足库恩-塔克条件时，极大似然估计值收敛，即求出非参数估计结果。

2.区间删失数据的非参数检验

针对 g组（g≥2）区间删失数据［1］，设 hl（t）为第 l组在时间 t的风险函数，l＝1，2，3，…，g，其中 t（l）为第 l组的生存时间。

即有如下假设，

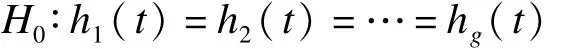
H1∶各组死亡率 hl（t）不等或不全相等，l＝1，2，3，…，g

利用非参数极大似然估计函数公式（1）L（p），可求出得分统计量 U＝（U1，U2，…，Ug），第 l组的得分统计量Ul可表示为:为权重，cjl表示在原假设下第 l个组在区间（τj－1，τj］内的死亡人数的期望值。cj表示第j个区间内的总死亡人数的期望值，类似地ajl和aj表示危险集的期望值，构造检验统计量χ2＝U∑U′，服从自由度为g-1的卡方分布。其中，∑为U的协方差矩阵，可通过置换方法（permutation method）得到［10］。针对 U统计量的不同权重 wj，主要有 Sun模型与 Wilcoxon-type模型［2］，其权重分别为wj＝1和wj＝（tj－1）。

3.半参数估计的区间删失ICM算法的Cox模型

基于所有个体的观测时间t，风险函数h（t）、基线风险函数h0（t），当引入协变量Z及协变量系数β时，Cox比例风险函数的表达式为 h（t｜Z）＝h0（t）exp（βTZ），基线生存函数S0（t）与协变量Z及协变量系数β存在关系式 S（t｜Z）＝S0（t）exp｜（βTZ），此时，区间删失生存函数的对数极大似然函数变为:

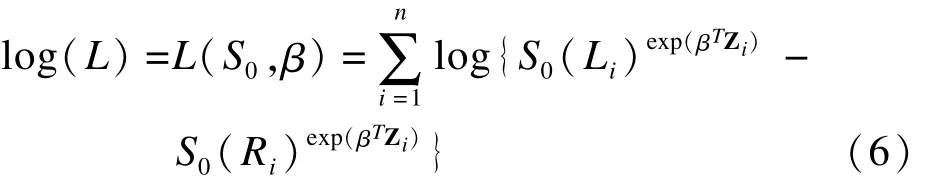
针对对数极大似然函数L（S0，β），可利用ICM（iterative convex minorant）算法进行迭代计算［11］。参数的初始值转化为右删失数据通过经典比例风险模型计算得出，并将Breslow估计值作为基准风险h0（t）的初始值。在对β进行显著性检验，使用轮廓似然法和信息矩阵等方法都能估算出的方差。但由于生存数据计算量大，以上方法迭代较慢，bootstrap方法成为一个较好的选择。Efron在1986年的随机模拟中发现［2］，在不同的删失率下，bootstrap方法计算速度快，且能保持较小的偏倚。因此综合考虑采用bootstrap方法进行方差估计。

实例分析

对某戒毒中心的881名静脉注射毒品患者经过戒毒治疗后的HIV感染数据进行分析［6］，此研究的起始时间为戒毒治疗的开始，事件为发生HIV感染。HIV病毒直接的感染情况可通过定期的血清检测来确定，以血清检测由阴转阳的时间来确定HIV感染。在该研究中，研究中心以月为单位定期检测血清情况。因事件发生（HIV感染）的确切时间并不能被直接观察到，即可将这些患者感染HIV看作区间删失型数据，其删失区间的左端点为最近一次血清检测为阴性的时间，右端点为第一次血清检测为阳性的时间。若在观察期内未检测到血清抗体呈阳性，则该患者为右删失数据。如第694号个体，第一次检测为阳性的时间为第42月，在此之前最近一次血清检测阴性的时间为第29月，故 t694∈（29，42］。

在观察随访的881个样本中，707例为男性，174为女性；患者年龄的中位数为19岁，其中400例患者小于等于19岁，481例患者大于19岁。576例患者在观察期内感染HIV（事件发生），305例未感染（右删失）。另外，按研究的观察时间，我们将历期（calendar period）分为1972至1985年和1986至1997年两大组，分别为539例和342例。

实例分析中将对患者的生存时间进行非参数估计，并将性别、历期、年龄（分为小于等于19岁与大于19岁）作为3个因素，进行组间比较和多因素回归模型分析。

1.生存率的非参数估计

对于HIV抗体由阴转阳情况，利用中点算法、Turnbull算法、修正EM算法，对患者的生存时间进行非参数估计，其生存率的比较见图1A。Turnbull算法与修正EM算法计算出的生存曲线除在尾部有些许差异，其余几乎重合。此外，类似于 Dorey［3］等人，将删失区间的中点当作右删失时间点，用Kaplan-Meier估计法进行计算，得到生存曲线，结果显示，中点处理后的生存率大体较高于Turnbull方法与修正EM算法，特别是在前期。不同的分组变量的生存率（图1B、1C、1D）估计亦显示中点算法得到的生存率大体上要高于修正EM算法得到的生存率。

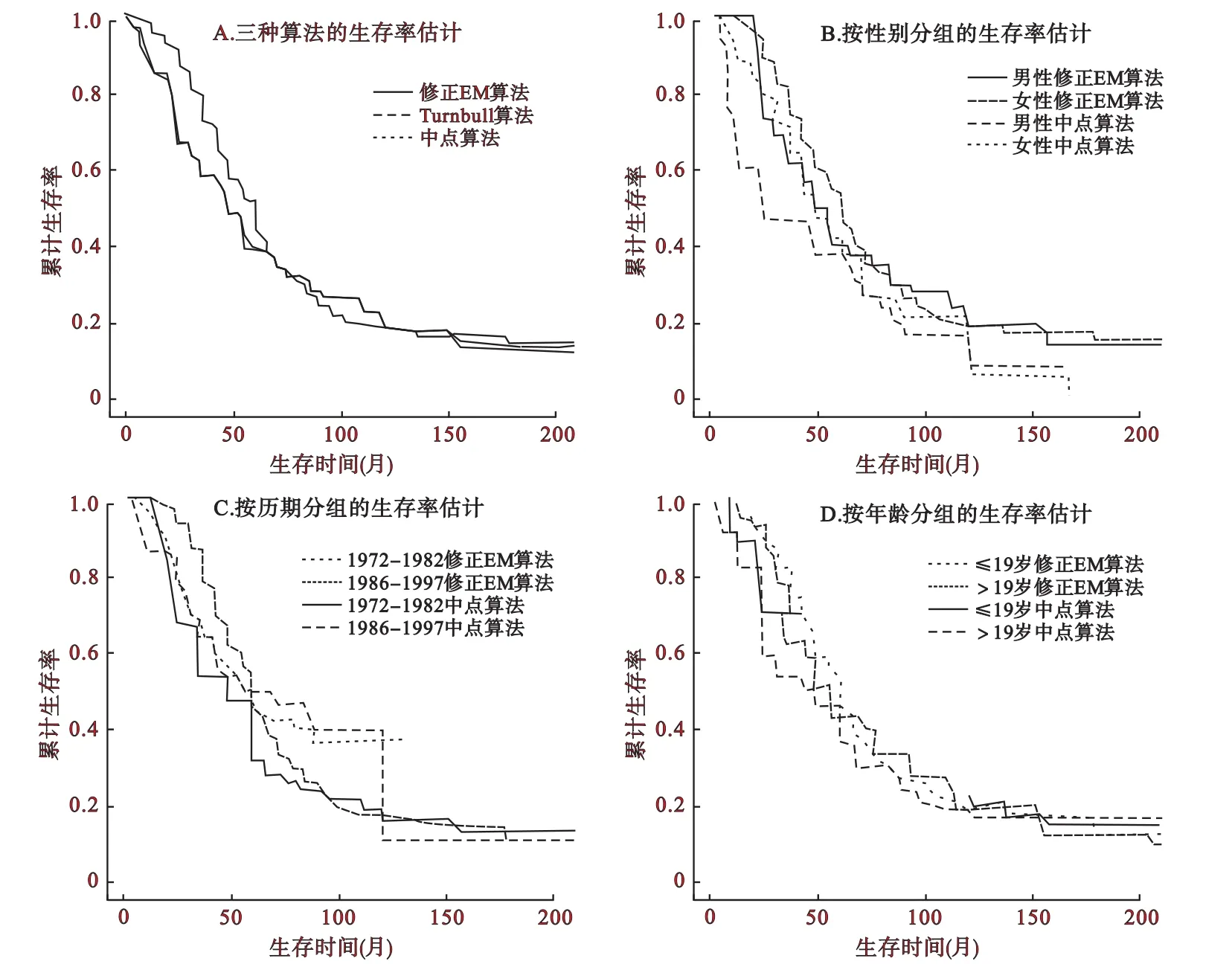
图1 三种方法所得生存率估计的总比较及分亚组比较

2.以性别、历期、年龄为分组因素分别做组间比较

采用权重为1的Sun模型，以历期为分组因素，进行组间比较，可得出检验统计量Z＝3.456，P＝0.001，显示不同的历期间生存率有统计学差异。若对生存时间取中点化为右删失数据后，使用log-rank检验比较组间差异，则得χ2＝0.083，P＝0.773提示差异没有统计学意义。但是，结合图1C可看出两个历期的生存率是不同的，从侧面上反映了1986年前进入戒毒中心的患者比1985年后进入的患者更容易感染HIV病毒。按性别分组，进行组间比较，两种算法均显示有统计学差异，从图1B中也可以看出，男性的生存率明显高于女性。由图1D可知，年龄分组基本没有差异，特别是中点算法，两条生存曲线基本重合，两种算法的组间比较亦显示没有统计学差异，P值均大于0.05。

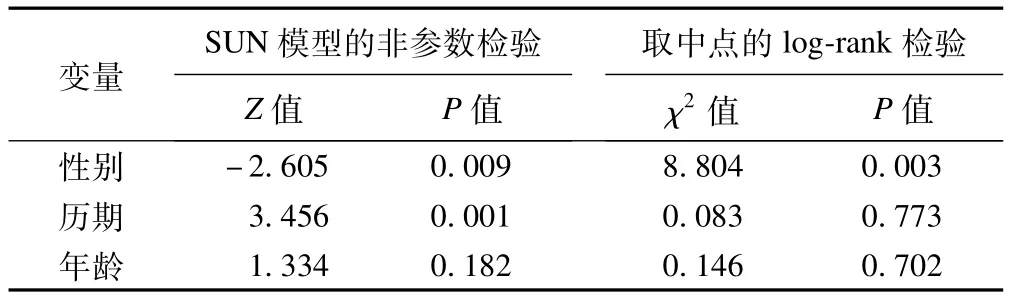
表1 SUN模型与取中点的log-rank的组间比较结果

3.以性别、历期、年龄作为分组因素做半参数回归模型

通过ICM算法，对患者的性别、历期、年龄分组进行半参数估计，计算参数β，并用bootstrap方法进行40000次有放回抽样，得出β的95%置信区间。此外，将区间中点转换为右删失数据，并计算其Cox模型参数。如表2所示，两种算法均显示不同性别的HIV感染情况有统计学差异，女性比男性更容易感染HIV病毒，图1B亦可看出男性的生存曲线明显分离高于女性的；年龄之间显示生存率没有统计学差异，两种算法的95%置信区间均包含了0；对于历期，虽然取中点的Cox比例风险模型中历期的置信区间包含0，提示不同的历期之间的HIV感染情况没有统计学差异，但是从图1C中可以看出，不同历期之间的生存率差异还是比较大的，同时，ICM算法的Cox模型显示不同历期的生存率是有统计学差异的，所以在这里取中点的Cox比例风险模型应用于区间删失数据的分析并不是很合理。

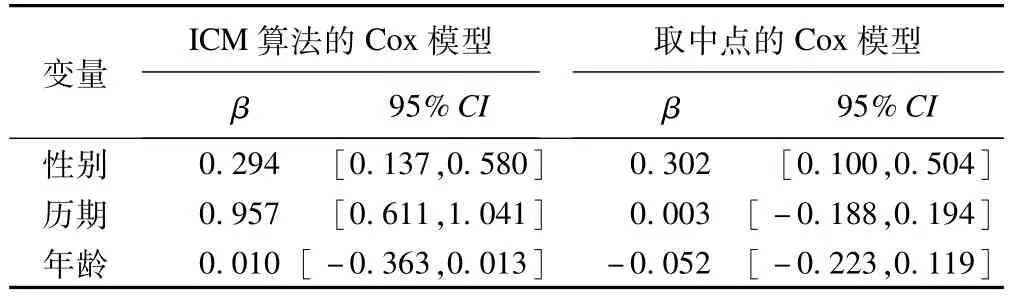
表2 ICM算法与取中点Cox模型的参数估计及95%置信区间

讨 论

区间删失数据在医学领域中是一种常见的数据类型，但是医务工作者常将其简化成右删失的形式，再采用Kaplan-Meier估计、Log-rank方法、Cox比例风险模型进行统计分析，从本文实例分析以及 Dorey［3］与Rücker［4］等人所做相关模拟可知，区间删失数据若简化成右删失的形式，会造成不合理的结果，因此对于区间删失数据处理，采用专门的分析方法是十分必要的。

本文所介绍的区间删失数据属于II型区间删失数据［12］。抽涉及的非参数估计、组间比较、半参数回归模型是较为主流的方法，几乎都能通过现行的SAS软件、R软件进行实现，例如本文使用R软件的interval，intcox等程序包，能够为行业内相关人士在具体的研究当中提供一定的帮助，得出更合理的估计、以及恰如其分的统计学结论。

［1］Fay MP，Shaw PA.Exact and asymptotic weighted log-rank tests for interval censored data:the interval R package.Journal of Statistical Software，2010，36（2）:i2.

［2］Mongoué-TchokotéS，Kim J.New statistical software for the proportional hazards model with current status data.Computational Statistics＆Data Analysis，2008，52（9）:4272-4286.

［3］Dorey FJ，Little RJA，Schenker N.Multiple imputation for threshold crossing data with interval censoring.Statistics in Medicine，1993，12（17）:1589-1603.

［4］Rücker G，Messerer D.Rem ission duration:an example of interval censored observations.Statistics in Medicine，1988，7（11）:1139-1145.

［5］Gómez G，Luz Calle M，Egea JM，et al.Risk of HIV infection as a function of the duration of intravenous drug use:a non-parametric Bayesian approach.Statistics in Medicine，2000，19（19）:2641-2656.

［6］Hanson MA.Invexity and the Kuhn-Tucker Theorem.Journal of Mathematical Analysis and Applications，1999，236（2）:594-604.

［7］Peto R.Experimental survival curves for interval-censored data.Journal of the Royal Statistical Society.Series C（Applied Statistics），1973，22（1）:86-91.

［8］Turnbull BW.Nonparametric estimation of a survivorship function with doubly censored data.Journalof the American Statistical Association，1974，69（345）:169-173.

［9］Gentleman R，Geyer CJ.Maximum likelihood for interval censored data:consistency and computation.Biometrika，1994，81（3）:618-623.

［10］Heinze G，Gnant M，Schemper M.Exact log-rank tests for unequal follow-up.Biometrics，2003，59（4）:1151-1157.

［11］Pan W.Extending the iterative convex m inorant algorithm to the Cox model for interval-censored data.Journal of Computational＆Graphical Statistics，1999，8（1）:109-120.

［12］梁洁，王彤，崔燕.II型区间删失数据的生存分析.中国卫生统计，2016，33（2）:357-361.

国家自然科学基金（81202288）；广州市科技计划（2012J5100023）；广东省科技计划（2010B031600100）

1.南方医科大学公共卫生学院生物统计学系、广东省热带病研究重点实验室（510515）

2.暨南大学经济学院统计学系

＃共同第一作者

△通信作者:陈征，E-mail:zchen@smu.edu.cn

（责任编辑:郭海强）