样本量估计及其在nQuery＋nTerim和SAS软件上的实现——群随机试验（二）

南方医科大学公共卫生学院（510515） 曹颖姝 孙亚清 陈平雁

·专题研究·

样本量估计及其在nQuery＋nTerim和SAS软件上的实现
——群随机试验（二）

南方医科大学公共卫生学院（510515） 曹颖姝 孙亚清 陈平雁△

7.2 两个率的比较

7.2.1 完全随机设计的差异性检验

方法:Donner＆Klar（2000）［3，5］提出的两个率差异性检验的群随机设计样本量估计建立在大样本正态近似理论基础上，其检验效能公式为:

式（7-3）和（7-4）分别为双侧和单侧检验。式中，δ1为备择假设下两组的率差，δ0为原假设下两组的率差，σTestType表示用某一种方法计算的标准误，TestType有三种方法供选择，分别是 Farrington and Manning Test（Likelihood Score）、Unpooled Test和 Pooled Test，式中σUnpool是Unpooled Test方法估计的标准误，如不做特殊说明，下文的含义相同。

在计算群数（群样本量）时，需给定群样本量（群数），首先设定群数（群样本量）的初始值，然后迭代群数（群样本量）直到满足设定的检验效能为止。此时的群数（群样本量），即研究所需的最小群数（群样本量）。差异性检验部分同时给出计算群数和群样本量的实例，等效性和非劣效性部分只给出计算群样本量的实例，计算群数的实例可参照差异性检验部分。

［例7-4］某试验欲评价中学控烟教育是否会降低青少年吸烟率，采用完全随机设计，将学校作为群。试验组接受控烟教育，对照组无干预。预期两年后试验组吸烟率为4%，对照组为6%。设定每所中学有100人参加，群内相关系数为0.01，试验组和对照组的群数和群样本量均相等，双侧检验水准为0.05，试采用Likelihood Score方法估计检验效能为80%时所需中学数量及总样本量［3］。

nQuery＋nTerim 4.0实现:

设定检验水准α＝0.05，采用双侧检验，检验效能取1-β＝80%。

在nQuery＋nTerim 4.0主菜单选择:

Goal:⊙ Cluster Randomized

Number of Groups:⊙ Two

Analysis Method:⊙ Test

方法框中选择:CRT Two Proportions Inequality Completely Randomized

在弹出的样本量估计窗口计算框中选择:Calculate required treatment group cluster（K1）given power and number of clusters，将各参数值键入（K2输入框中键入K1），结果如图7-7所示，即每组需要38所中学，每所需随机抽取100名学生，本研究总的样本量为7600人。

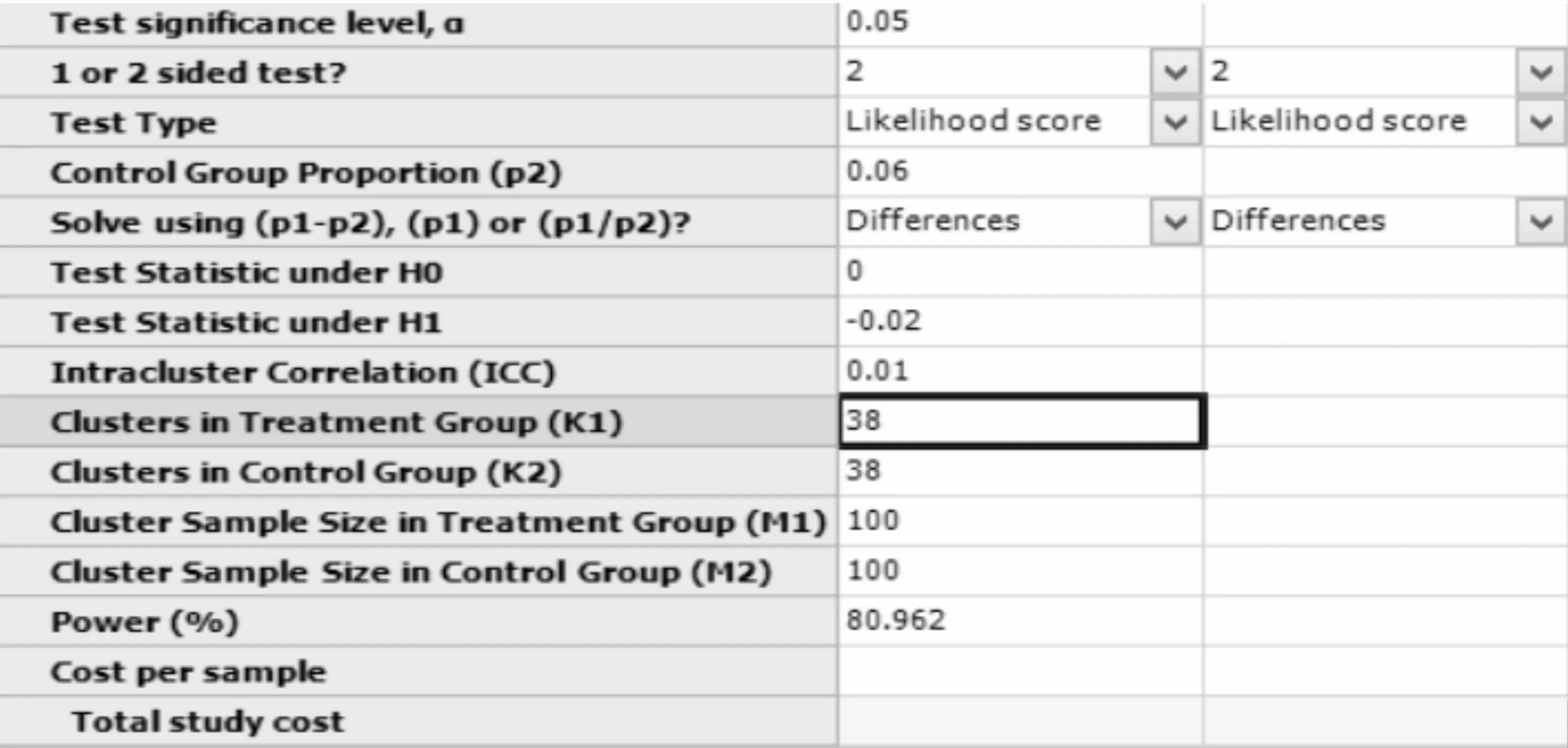
图7-7 nQuery＋nTerim 4.0关于例7-4样本量估计的参数设置与计算结果

SAS9.4软件实现:

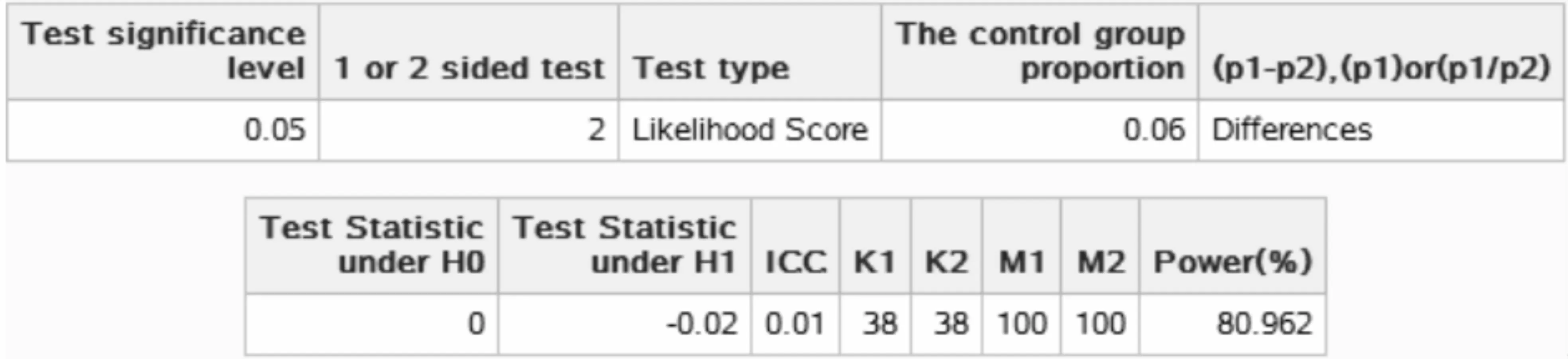
图7-8 SAS 9.4关于例7-4样本量估计的参数设置与计算结果

［例7-5］研究背景同例7-4。设定试验组有40所中学参加，对照组有20所中学参加，对照组每所学校的参加人数是试验组的2倍，其余参数设置与例7-4相同，试采用Unpool方法估计检验效能为80%时每所中学所需的学生数及总样本量。

nQuery＋nTerim 4.0实现:

设定检验水准α＝0.05，采用双侧检验，检验效能取1-β＝80%。

主菜单和方法框的选择同例7-4。

在弹出的样本量估计窗口计算框中选择:Calculate required treatment sample size（M1）given power and number of clusters，将各参数值键入（M2输入框中键入2M1），结果如图7-9所示，即试验组需要40所中学，每所随机抽取179名学生，对照组需要20所中学，每所需随机抽取358名学生，本研究总的样本量为14320人。

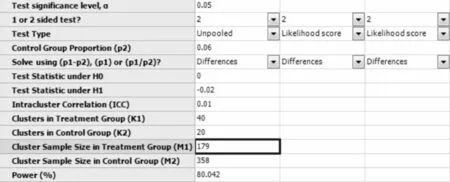
图7-9 nQuery＋nTerim 4.0关于例7-5样本量估计的参数设置与计算结果

SAS9.4软件实现:

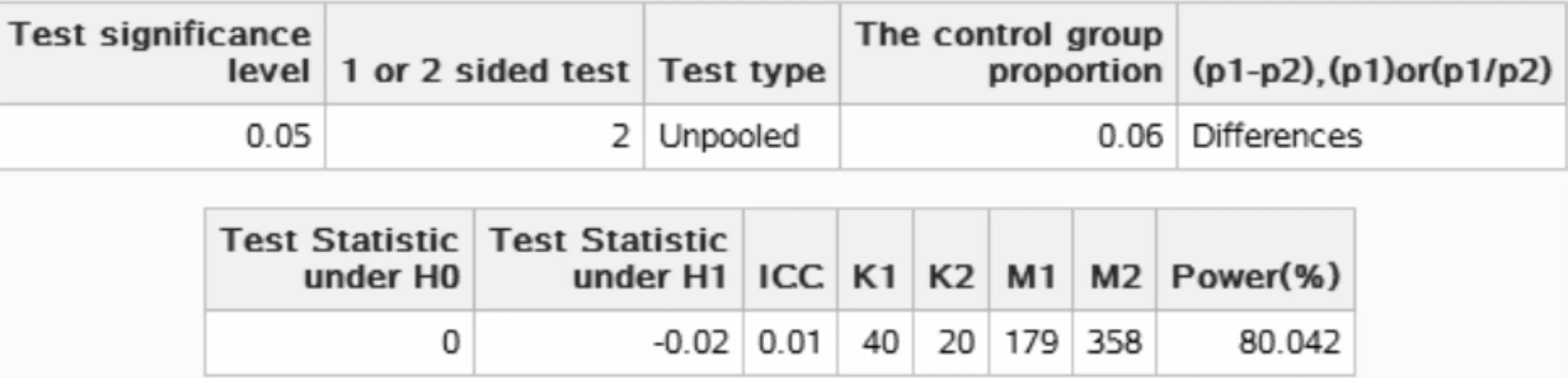
图7-10 SAS 9.4关于例7-5样本量估计的参数设置与计算结果

7.2.2 完全随机设计的等效性检验

方法:Donner＆Klar（2000）［3，5］提出的两个率等效性检验的群随机样本量估计建立在大样本正态近似理论基础上，其检验效能公式为:

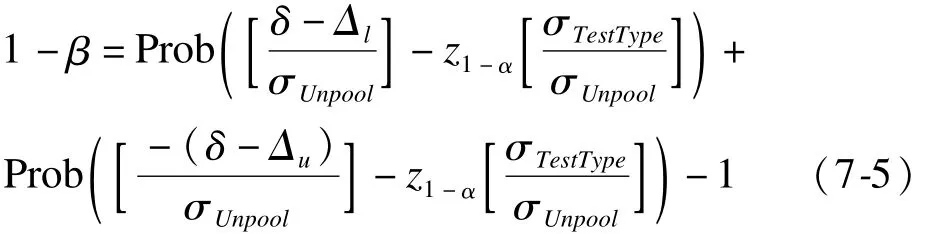
式中，Δl为等效性界值下限，Δu为等效性界值上限，等效性界值即应用方面可以接受的试验组和对照组总体阳性率的差值，δ为预期两个总体阳性率之差。

在计算群数（群样本量）时，需给定群样本量（群数），首先设定群数（群样本量）的初始值，然后迭代群数（群样本量）直到满足设定的检验效能为止。此时的群数（群样本量），即研究所需的最小群数（群样本量）。

［例7-6］某研究欲评价护理艾滋病患者的两种抗病毒策略是否等效，采用完全随机设计，以划分出的各个地理区域作为群，试验组采用家庭护理，对照组采用诊所护理。设定两组护理策略的抗病毒失败率为20%，等效性界值为9%。假定试验组和对照组的群数和群样本量均相等，群数为20，群内相关系数为0.002，设定检验水准为0.05，试采用Likelihood Score方法估计检验效能为95%时每个区域所需的患者数及总样本量［6］。

nQuery＋nTerim 4.0实现:

设定检验水准α＝0.05，检验效能取1-β＝95%。

在nQuery＋nTerim 4.0主菜单选择:

Goal:⊙ Cluster Random ized

Number of Groups:⊙ Two

Analysis Method:⊙ Test

方法框中选择:CRT Two Proportions Equivalence Completely Random ized。

在弹出的样本量估计窗口计算框中选择:Calculate required treatment sample size（M1）given power and number of clusters，将各参数值键入，结果如图7-11所示，即每组需要20个地理区域，每个区域需随机抽取28名艾滋病患者，本研究总的样本量为1120人。

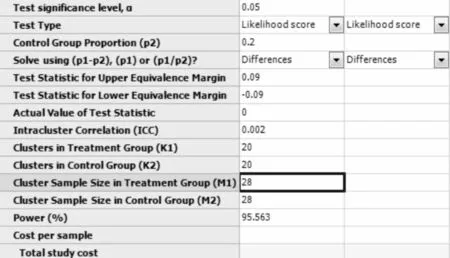
图7-11 nQuery＋nTerim 4.0关于例7-6样本量估计的参数设置与计算结果

SAS9.4软件实现:

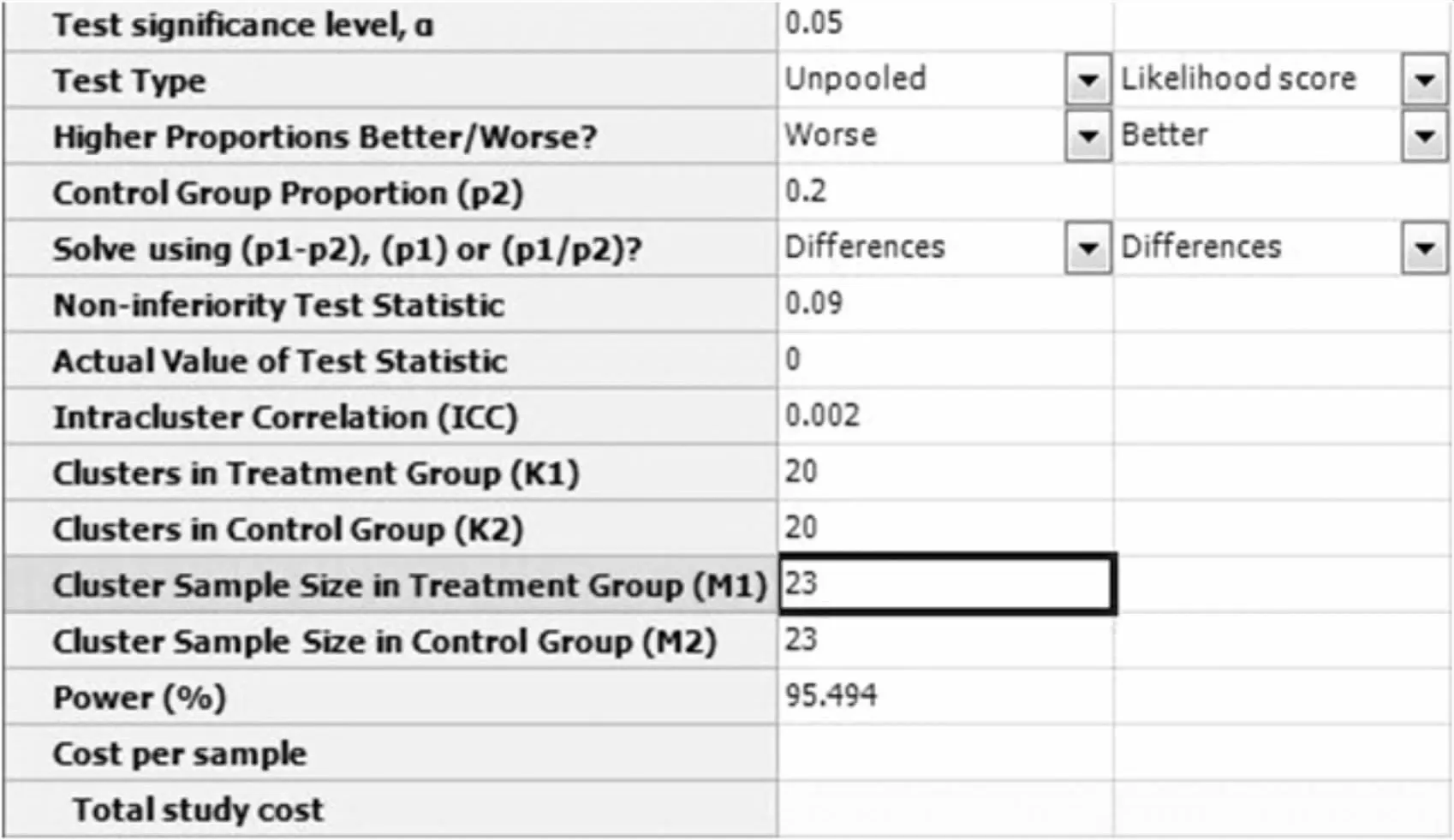
图7-12 SAS 9.4关于例7-6样本量估计的参数设置与计算结果

7.2.3 完全随机设计的非劣效检验（试验组-对照组）

方法:Donner＆Klar（2000）［3，5］提出的两个率非劣效性检验的群随机设计样本量估计建立在大样本正态近似理论基础上，其检验效能公式为:

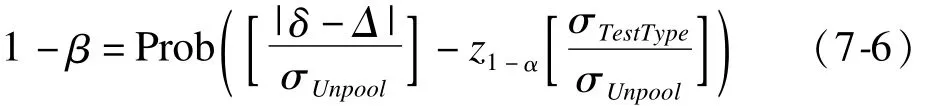
式中Δ为非劣效界值，δ为预期的率差。

在计算群数（群样本量）时，需给定群样本量（群数），首先设定群数（群样本量）的初始值，然后迭代群数（群样本量）直到满足设定的检验效能为止。此时的群数（群样本量），即研究所需的最小群数（群样本量）。

本方法同样适用于优效性检验，将式（7-6）中Δ定义为优效界值即可。当Δ为0时，即为差异性检验，式（7-6）演化为式（7-4）。

［例7-7］研究背景同例7-6，假设非劣效界值为0.09，其余参数设置相同，试采用Unpool方法估计每个区域所需的患者数及总样本量。

nQuery＋nTerim 4.0实现:

设定单侧检验水准α＝0.05，检验效能取1-β＝95%。

在nQuery＋nTerim4.0主菜单选择:

Goal:⊙ Cluster Random ized

Number of Groups:⊙ Two

Analysis Method:⊙ Test

方法框中选择:CRT Two Proportions Non-Inferiority Completely Randomized。

在弹出的样本量估计窗口计算框中选择:Calculate required treatment sample size（M1）given power and number of clusters，将各参数值键入，结果如图7-13所示，即每组需要20个区域，每个区域需随机抽取23名艾滋病患者，本研究总的样本量为920人。

图7-13 nQuery＋nTerim 4.0关于例7-7样本量估计的参数设置与计算结果

SAS9.4软件实现:

图7-14 SAS 9.4关于例7-7样本量估计的参数设置与计算结果

△通信作者:陈平雁

（责任编辑:郭海强）