基于趋势外推与ARIMA预测我国医院诊疗及住院人次*

李望晨 崔庆霞 张利平△

基于趋势外推与ARIMA预测我国医院诊疗及住院人次*

李望晨1，2，3崔庆霞1，2，3张利平1，2，3△

目的探索我国医院诊疗与入院人次预测建模方案并比较其差异。方法借助SPSS、SAS软件，以曲线拟合和ARIMA法建立模型进行拟合与预测。结果我国医院诊疗与入院人次数据均符合二次曲线变化，拟合与预测效果好；ARIMA法对二阶差分后平稳序列建模未见更优性能，其拟合性能与数据段选取无明显联系。结论数据预分析和方法适配很有必要；ARIMA法在时间序列分析领域有普适代表性，适于随机长期序列建模；传统曲线拟合法对于趋势平滑数据具有优良性能。

诊疗人次 住院人次 预测 曲线拟合 ARIMA

预测研究是根据过去或现在资料推断未来的发展状况，可以为决策提供依据。时间序列法对随时间变化的时序资料进行拟合，旨在反映现在或过去规律，预测未来情况。医院诊疗与住院人次是衡量医疗服务效能的指标，有必要根据数据资料研究其变化规律并推测未来。基于我国诊疗和住院人次数据的延续性特点，可以考虑以时间为自变量进行拟合或由序列间的短期自相关性建立模型。

基本方法

医院诊疗和入院人次资料随机波动小、变化较稳定，可以选择利用趋势外推法［1］和 ARIMA法［2－4］建模，根据历史资料进行纵向拟合和预测，为医疗服务与卫生决策提供实证参考或方法借鉴。

趋势外推法一般指曲线拟合法，如直线拟合、多项式曲线、指数曲线、生长曲线等。其基本思想是针对时序资料的趋势变化特点，优选并建立拟合模型进行外推预测，它要求数据变化规律应大致符合曲线特点，即符合以时序值为自变量的函数yt＝f（t），t为时序。

ARIMA（p，d，q）用于平稳序列拟合及预测，其中p和q分别为自回归和移动平均阶数，d为差分次数，其表达式为（1－φ1B－…－φpBp）（1－B）dxt＝（1－θ1B－…－θqBq）εt，其中 Bxt＝xt－1为延迟算子，｛xt｝为原始序列，｛εt｝为残差序列，φi、θj为参数。先对原始序列进行纯随机性、平稳性检验，纯随机序列没有研究价值，趋势性或周期性变化序列要差分变换为平稳序列。根据样本自相关图、偏自相关图以及中间检验结果判定拟合优度，估计参数和识别模型，拟合时序规律后用于推测未来。

2 实证分析

《中国卫生统计年鉴》给出我国医院诊疗和住院人次指标资料，统计指标包括总诊疗人次X1、综合医院诊疗人次 X2、中医医院诊疗人次X3、门急诊人次X4、综合医院门急诊人次X5、中医医院门急诊人次X6、总入院人数（万人）X7、综合医院入院人数X8、中医医院入院人数X9、每百门急诊入院人数（人）X10。

对诊疗人次指标X1～X6进行散点图观察分析，2003年前数据变化不大，此后有较显著递增趋势。原始数据见表1。

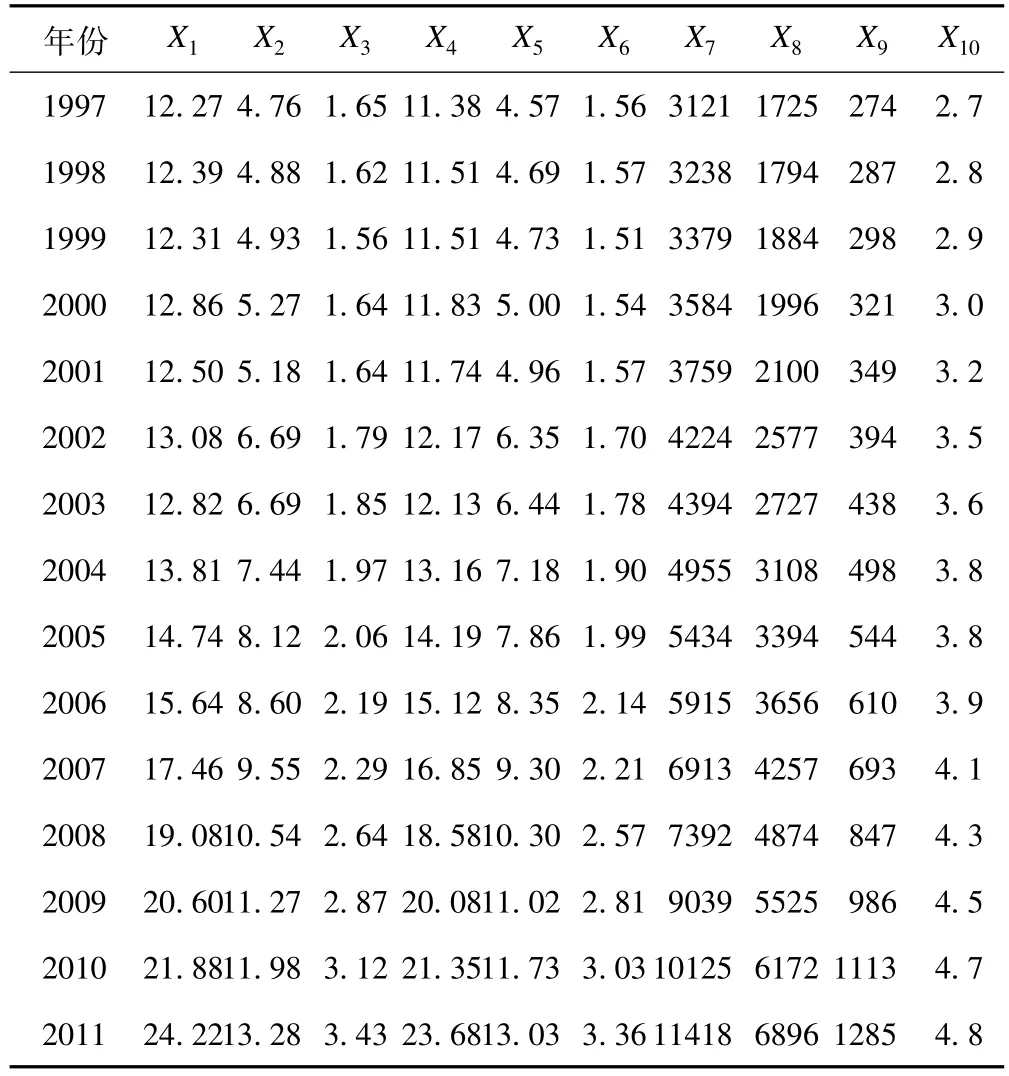
表1 1997－2011年诊疗与入院人次统计资料

1997－2010年数据变化呈平稳递增特点，可用趋势外推法对2011年数据进行预测研究。利用SPSS软件实现曲线拟合，可点选全部曲线类型纳入建模过程。经综合对比，二次曲线或三次曲线拟合效果较好。

根据SPSS软件得到总诊疗人次二次曲线yt＝13.194－0.599t＋0.088t2，三次曲线 yt＝12.727－0 279t＋0.037t2＋0.002t3，据分析两者拟合效果几乎相同。经模型检验并分析拟合指标，计算决定系数并进行F检验。对于二次曲线来说，决定系数R2为0.989，F检验统计量517.986，P值 ＜0.0001，说明拟合效果有统计学意义；对于三次曲线来说，决定系数为0.991，F检验统计量357.800，P值 ＜0.0001，说明拟合效果有统计学意义。经比较两种模型相差不大，三次曲线略微好些。

对各指标逐次进行建模验证，也发现较显著的曲线变化规律，而且二次曲线和三次曲线也可作为诊疗和住院指标拟合曲线模型。同法对指标X1～X10独立进行拟合。两种研究思路分别记为二次曲线、三次曲线建模方案I－A、I－B。ARIMA法适于平稳序列拟合建模分析，非平稳序列应差分消除趋势特征。二次曲线序列yt一阶差分ut仍有趋势性，二阶差分u（2）t为常数、无趋势，二次曲线变化序列可经二阶差分化为平稳序列，三次曲线也可经三阶差分化为平稳序列。

根据SAS软件，实现医院总门诊人次建模拟合过程，经计算原始序列为非白噪声、非平稳序列，它有相关性和递增趋势特点，原始序列经二阶差分后才能达到平稳。

采用条件最小二乘法进行模型拟合计算，确定二阶移动平均模型 MA（2）为最优模型:（1－B）2yt＝（1－θ1B＋θ2B2）εt。其中 θ1＝0.76191，t值为 4.44，P值为0.0013＜0.05；θ2＝－0.98380，对应 t值为 －5.70，P值为0.0002＜0.05，说明参数计算结果均有统计学意义。AIC为16.827，SBC为17.797。经过残差自相关性检验，发现延迟6期时卡方统计量为1.59，自由度为4，P值为0.8110＞0.05，自相关系数分别为 －0.022，0.020，－0.171，－0.016，0.011，－0.191。说明该模型对原始序列信息提取的效果很好，残差序列已经没有任何相关信息可提取，为白噪声序列，模型对原序列拟合很好，可进行预测，经外推得出1～5期的预测值依次为 23.22，24.32，25.42，26.52，27.61。由于时间序列适于短期外推，随时间延迟预测误差大、参考价值小，因此，2011年预测值取23.22。后期预测值可不断引入新数据后重新建模。

须补充说明，若认为原始数据序列符合三次曲线特点，三阶差分后用于建立模型，经验证，发现拟合效果和预测值大致相同，故没必要考虑该建模方案。

首先，根据1997－2010年连续数据段制定基于ARIMA法的建模方案II-A，可以依次分别建立各项指标 X1～X10的拟合模型，令 yt＝（1－B）2xt。表达式依次列出如下:

然后，借助SAS软件，仍采用ARIMA法，针对所有指标分别截取不同数据段建立模型、验证性能差异。忽略早期部分数据影响，截取2003－2010年连续数据段组成建模方案II-B；如果再以2004－2010年数据建立模型，因数据太少而无法实现ARIMA法预测建模，予以舍弃；追加补录长期的1980－2010年共31个连续数据段组成建模方案II-C。在方案II-A、II-B、II-C实施过程中，分别以X1～X10各指标时序资料独立进行建模，过程不再赘述。

最后，将全部多种时间序列数据段截取，分别用曲线拟合法和ARIMA法建模，将X1～X10各指标真实值、预测值及相对误差情况最终分析结果汇总比较，见表2。

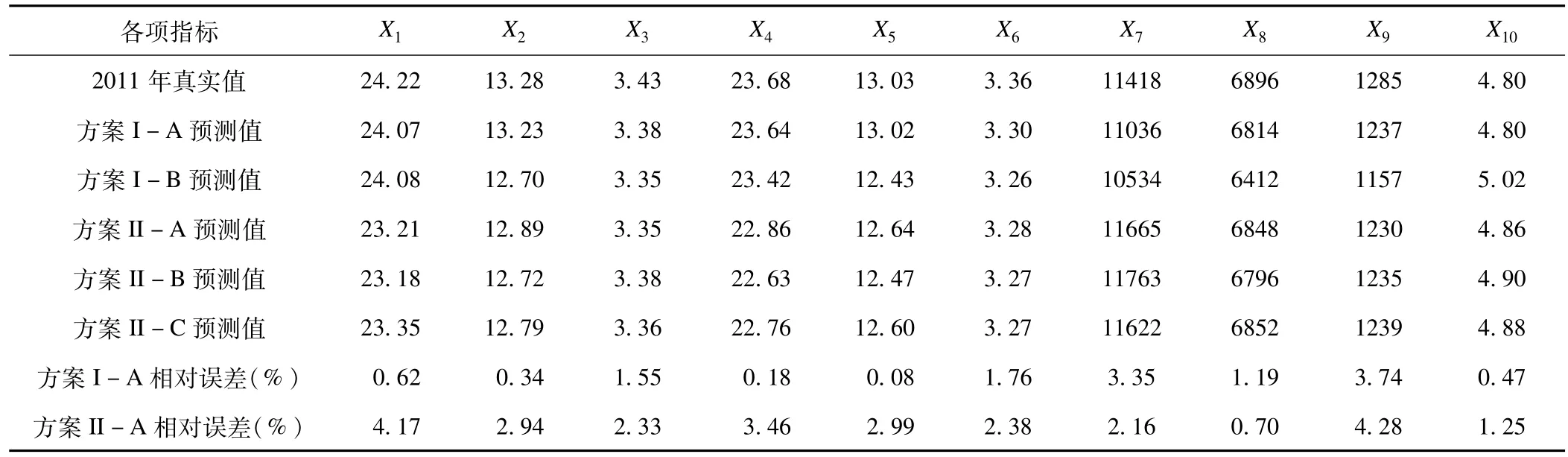
表2 不同建模方案预测值与真实值比较

我国诊疗与住院人次各指标数据随年份呈现较明显的二次曲线变化特点，趋势变化明显。对X1～X10各指标来说，经散点图初步分析发现数据随时间大致有相似变化特点，可考虑同类建模方法。从拟合过程可知，方案I-A、I-B拟合效果差异不大，但I-A外推效果好些；方案II-A、II-B与II-C相比，拟合与外推效果差异不大；方案I拟合与外推简单且效果好，二次曲线对诊疗人次指标预测更好，ARIMA模型对住院人次指标预测更好，二者均有代表性。我国医院诊疗与住院人次各指标数据有趋势性和平滑性，可以用简单曲线拟合技术与经典ARIMA法对其进行时间序列拟合建模。

讨 论

诊疗与住院人次的影响因素复杂，时间序列模型适于事物自身的时序变化规律拟合和短期预测。医院诊疗和入院人次数据变化平滑且有递增趋势，若假设此规律延续于未来，可建模拟合纵向规律并进行外推预测，为指导卫生工作提供参考。曲线模型适于拟合增长数据平滑变化趋势，其中二次或三次曲线适合前期变化小而后期呈递增趋势的数据。ARIMA法为平稳序列建模经典方法，常需较丰富资料，它对随机性波动数据建模更具代表性。

从1997－2010年我国医院诊疗和住院人次资料早期数据随时间变化小，后期趋势显著且变化稳定，其规律更符合二次或三次曲线特点。ARIMA法采用经典原理，具有普适性和代表性，建模时需较充分资料，拟合长期不规则规律更显优势。本例尝试用不同历史数据段建立模型，未发现预测效果敏感变化。除外，资料中各指标数据平滑变化，有明显早期平缓而后平滑的趋势特点，简单曲线拟合法对该特定资料表现了优良性能，这与ARIMA模型作为一般随机波动性长时资料拟合分析的经典方法并不矛盾。鉴于我国医院诊疗与门诊人次系列指标数据特有的趋势性与平滑性特点，简单曲线拟合法和ARIMA法都适于拟合外推建模，以预测未来状况和指导卫生决策。

［1］徐国祥.统计预测与决策.上海财经大学出版社，2008:129-168.

［2］王燕.应用时间序列分析.中国人民大学出版社，2013，18-134.

［3］刘刚，唐宋，孙文杰.时间序列分析法在香港结核病预测中的应用.中国卫生统计，2012，29（2）:226-228.

［4］马春柳，刘海霞，李小升.SARIMA模型在医院住院人次预测中的应用.中国卫生统计，2013，30（3）:432-433.

教育部人文社科基金15YJCZH087；山东自然科学基金ZR2015HL101；山东统计局课题KT15186，KT15187；山东卫计委课题2014WS0460

1.“健康山东”重大社会风险预测与治理协同创新中心

2.社会领域健康风险协同创新中心

3.潍坊医学院公共卫生与管理学院

△通信作者:张利平

（责任编辑:郭海强）