高维组学变量筛选方法的稳定性评价方法及应用*

哈尔滨医科大学卫生统计教研室（150086） 王璟涛 侯 艳 李 康

高维组学变量筛选方法的稳定性评价方法及应用*

哈尔滨医科大学卫生统计教研室（150086） 王璟涛 侯 艳 李 康△

目的在高维组学变量筛选过程中，当数据发生轻微变化时，变量筛选方法筛选出的变量会发生一定的变化。本文探索如何评价筛选变量的结果是否稳定。方法通过模拟实验，分析对比了HD、SCSR、TD、KI、CW、RCW六种稳定性评价方法的准确性及变异程度，并通过实例结合PLS、svmRFE和RF三种变量筛选方法对SCSR方法进行了考察。结果当变量排序为随机产生时，SCSR、KI和RCW三种方法基本能够在取各种变量数目情况下始终接近于最小值0。对于置换标签和变量值后的数据集，PLS、RF、svmRFE三种方法的稳定性几乎完全相同，SCSR、KI和RCW三种稳定性评价指标在取不同筛选阈值时都达到了最小期望值。在评价指标的稳定性上，HD和SCSR能够保持很小的变异，具有更好的稳健性。结论SCSR的准确性和稳定性最好，推荐作为稳定性评价指标。

组学 高维数据 变量筛选 稳定性

在高维组学研究中，变量筛选通常用于选择能够提高判别模型分类效果的最小变量子集。除了提高判别效果，在高维组学中，研究人员利用变量筛选方法剔除与疾病状态无关的噪声变量，筛选出与疾病状态紧密相关、对疾病状态具有一定预测价值的变量，并将这些变量作为潜在的生物学标志物。

在进行变量筛选时，为防止判别模型的过拟合，研究人员可以按照一定比例将数据集随机分为训练集和测试集，在训练集上进行变量筛选后，再利用测试集检验所筛变量对疾病状态的预测能力。通常，研究人员往往更加关注筛选出的变量用于判别模型后分类性能的提高，却经常忽略筛选变量结果的稳定性，这种不稳定性有可能降低潜在生物学标志物的可信程度。因此，在变量筛选应用中，对于特定的高维组学数据，研究评价不同变量筛选方法的稳定性，筛选出更为可靠的潜在生物学标志物十分必要。本文在介绍了六种变量筛选稳定性评价指标的基础上，对其特点进行研究，并结合实例分析为如何选择变量筛选方法提供一定的依据。

原理与方法

本文研究的稳定性是指变量筛选方法对于训练集轻微变动的敏感性。在目前的研究中，对于稳定性的评价通常是通过对变量筛选方法在不同训练集上筛选变量子集之间的一致性进行评价。

图1展示了评价稳定性的一般过程［1］:①对于给定的数据集，从其中抽取比例为e的样本形成子集，共抽取W次，得到W个样本子集D1，D2，……，DW；②对每个样本子集进行变量筛选，变量筛选结果以变量重要性排序的形式体现，保留每个变量排序结果中的前s个变量，得到 W个筛选变量子集:V1，V2，……，VW；③利用稳定性评价指标计算所有筛选变量子集中两两之间的一致性，得到一个一致性矩阵；④求所有一致性结果的均值，得到最终的稳定性评价结果。

其中，第③步是整个评价过程中的核心部分，目前有许多文章提出了评价两个筛选变量子集之间一致性的方法。

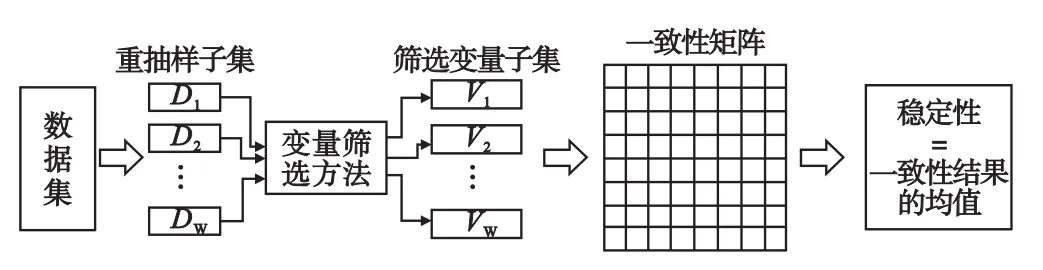
图1 变量筛选方法稳定性评价的一般过程

1.Hamming距离法

Kevin Dunne利用Hamming距离作为两个筛选变量子集之间的一致性评价指标［2］，其表达式为

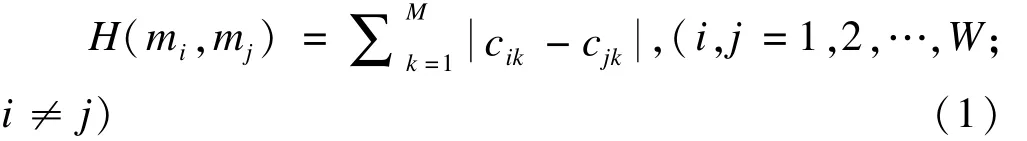
其中，M为原始数据集中变量的个数；mi，mj为所有筛选变量子集中的任意两个；cik表示所有变量中第k个变量被筛选变量子集mi纳入的情况，如果该变量被纳入筛选变量子集mi，则其值为1，否则其值为0。

然后，计算所有筛选变量子集两两之间的Hamming距离的均值，W个筛选变量子集两两之间共计算得到W（W－1）/2个Hamming距离，所以均值为

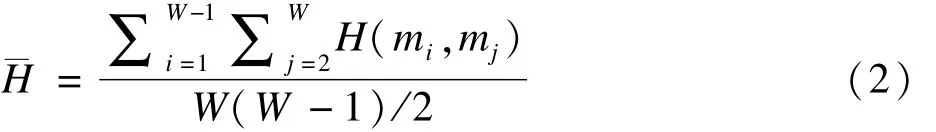
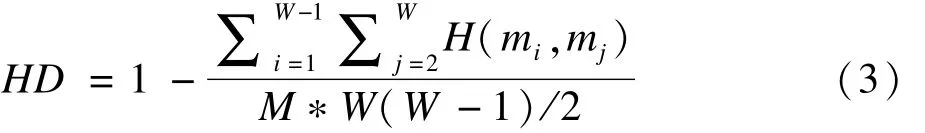
2.SCSR法

Barbosa提出将稳定性显著的变量（self-consisitent selections，SCS）个数与筛选变量子集长度的比值作为评价筛选方法稳定性的指标［3］，即 SCSR（self-consisitentselections ratio）。这里假设某个变量在所有筛选变量子集中被纳入的次数服从二项分布，二项分布的参数P等于筛选变量子集的长度与总的变量个数M的比值。设置检验水准为0.01，将出现次数高于该界值的变量当做SCS，利用Holm-Bonferroni校正多重检验的影响。然后计算每个筛选变量子集中SCS的个数与筛选变量子集长度的比值SCSR，将所有筛选变量子集的SCSR的均值作为评价指标。

3.Tanimoto距离

Kalousis使用Tanimoto距离作为筛选变量子集一致性的评价指标［4］，统计量的计算公式为

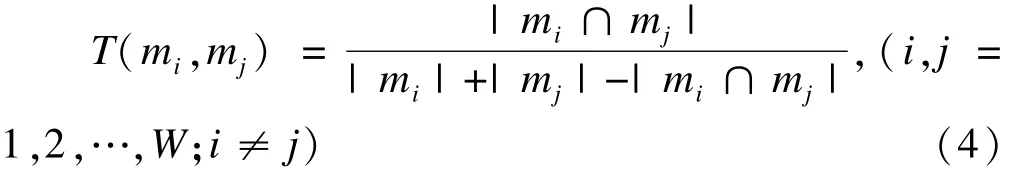
其中，分子为任意两个筛选变量子集交集的长度，分母为这两个筛选变量子集并集的长度。

然后，计算所有筛选变量子集两两之间Tanimoto距离的均值，作为作为变量筛选方法的稳定性的评价指标，即

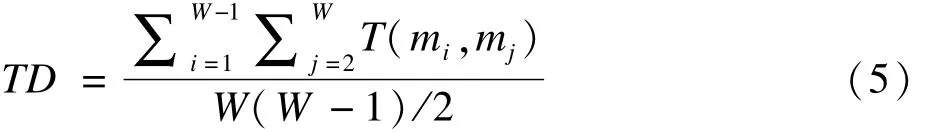
4.Kuncheva指数

在两个筛选变量子集的交集中，有一部分变量可能由于随机波动导致。对于两个长度相等的筛选变量子集，当一个筛选变量子集固定时，随机产生另一筛选变量子集，则两个筛选变量子集重合部分的变量个数服从超几何分布，其期望值为 s2/M。Kuncheva对Tanimoto距离法进行了改进，将这一部分变量从重合部分中剔除［5］，构造了两个筛选变量子集之间一致性的评价指标Ic，其表达式为

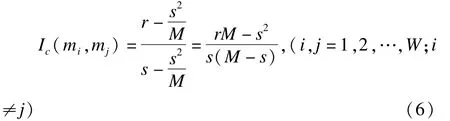
其中，s为每个筛选变量子集的长度，r为两个筛选变量子集的交集的长度，M为原始数据集中的变量个数。

然后，计算所有筛选变量子集两两之间的Ic的均值，作为作为变量筛选方法的稳定性的评价指标，即

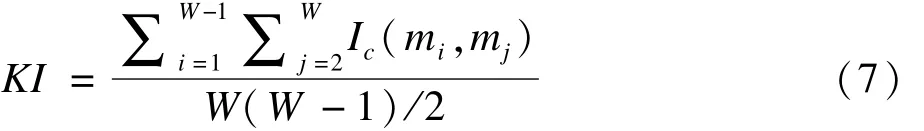
5.CW统计量

Somol将所有筛选变量子集中包含的变量进行综合考虑，记S为所有筛选变量子集中的变量构成的集合，筛选变量子集个数为W，每个筛选变量子集的长度均为s，所有变量出现的次数总和（即集合S的长度）为V＝W*s，集合S中出现的变量个数为A（A≤M），记 Ff为其中第 f个变量出现的次数（f＝1，2，…，A），因此所有变量出现的次数总和 V也等于引入了评价指标 C（S），即

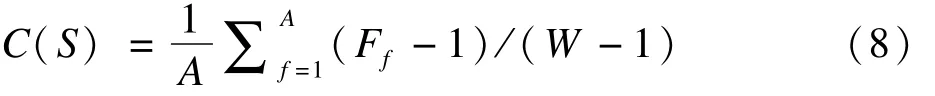
这一指标的含义是计算集合S中每个变量出现的次数与所有变量出现的总次数之比的均值。

然后，在指标 C（S）中的每一项乘以一个权重wf＝Ff/V，得到 CW指标［6］，用以衡量加权的一致性（weighted consistency），即

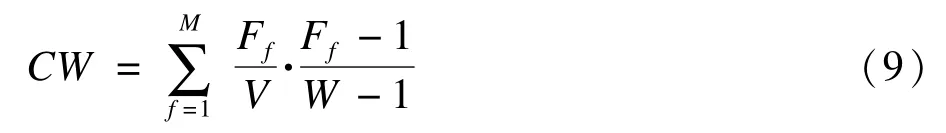
6.RCW统计量

上述CW未调整筛选变量子集个数W和原始数据集的变量个数M对一致性的影响，即随着W和M的增大，CW也会随之增大。为此，Somol计算出新的衡量指标，即首先在给定W和M的情况下CW的最大值和最小值

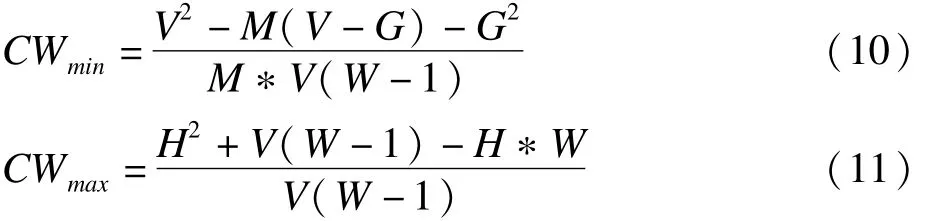
其中，G为V除以M后的余数，即G＝mod（V/M）；H为V除以W后的余数，即H＝mod（V/W）；然后利用最大值、最小值对CW进行调整，构建RCW指标［6］，用以衡量相对加权的一致性（relative weighted consistency），即

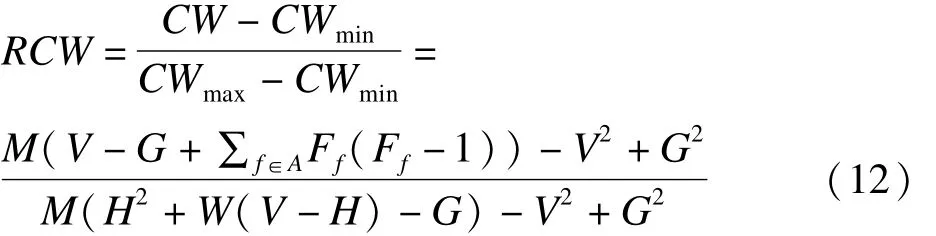
模拟实验

1.不同指标对于随机结果的评价能力

这里，模拟的方法是对1000个变量进行随机排序，然后分别取前 1%，5%，10%，15%，20%，25%，…，95%，100%的变量作为筛选变量子集，利用六种指标进行评价，重复100次，取其平均值。由于变量重要性的顺序在每次排列时是随机给出的，因此稳定性应接近最小期望值。结果显示，在六种评价方法中，KI、SCSR和RCW三种统计量值基本能够在取各种变量数目情况下始终处于最小值0附近，而其他三种方法则在变量选入数目不同时，统计量的值明显变化；TD和CW仅在取变量总数目的1%时，其值接近于0；HD则呈抛物线状，在任何情况下其值都不接近0（见图2）。

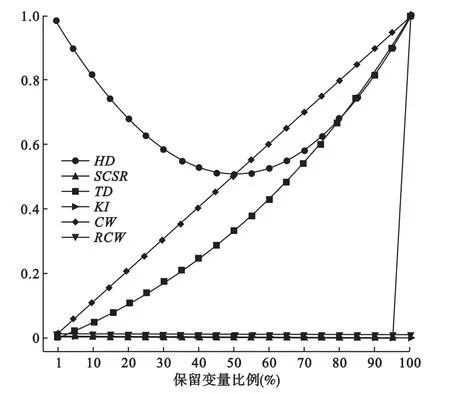
图2 各种评价指标对随机产生的筛选变量子集的评价结果

2.实际数据置换实验

取卵巢癌代谢组数据，其中有2106个变量，病例组140例，对照组158例。将是否患病的标签和变量值不断打乱，分别用偏最小二乘法（PLS）［7］、随机森林（RF）［8］、支持向量机后退法（svmRFE）［9］进行变量筛选，并保留前 1%，5%，10%，15%，20%，25%，…，95%，100%的变量作为筛选变量子集，重复100次，然后利用六种指标进行评价。结果显示，PLS、RF和svmRFE三种变量筛选方法的结果完全重合（见图3），而SCSR、KI和RCW三种稳定性评价指标在取不同筛选阈值时都达到了最小期望值，与前面的结果一致。

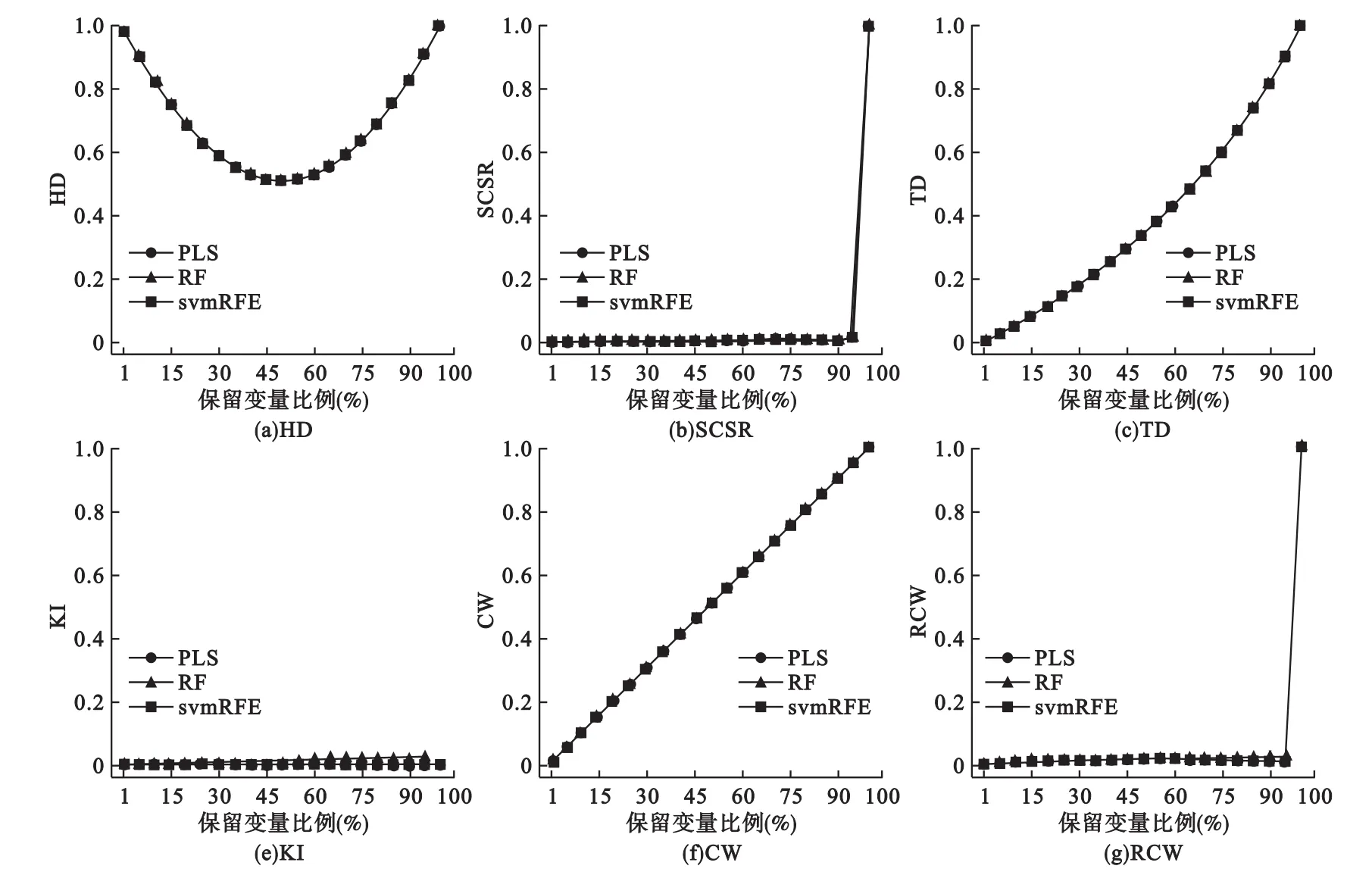
图3 各种评价指标对变量筛选方法在转换数据上的稳定性的评价结果

3.不同指标稳定性的对比研究

为了对六种指标的自身稳定性进行比较，本研究进行了如下模拟实验:模拟产生A、B两组数据，包含20个差异变量，A组差异变量服从N（0，1）的正态分布，B组差异变量服从N（1，1）的正态分布，任意两差异变量间的相关系数为ρ＝0.9；然后加入980个噪声（无差异变量），形成样本数据。样本量分别设置为30、50、100，计算各项指标的参数设置为 e＝0.9，W＝1000。考虑模拟的计算量较大，这里仅使用偏最小二乘（PLS）方法进行变量筛选，筛选的阈值分别取前1%、2%、3%、5%、10%、20%、50%的变量。上述过程模拟50次，然后分别计算六种指标的变异系数。结果表明:在六种评价方法中，HD和SCSR在不同情况下均十分稳定，变异系数恒接近0（图4）；KI、CW、RCW和TD则相对不够稳定，尤其在样本量较小情况（n＝30）时，变异较大（图4）。

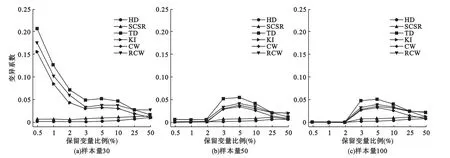
图4 不同指标的变异系数

实例分析

实例取自四个数据集，包括一个代谢组数据和三个基因表达数据（见表1）。现用SCSR方法分析比较PLS、RF、svmRFE三种不同变量筛选方法得到结果的稳定性。

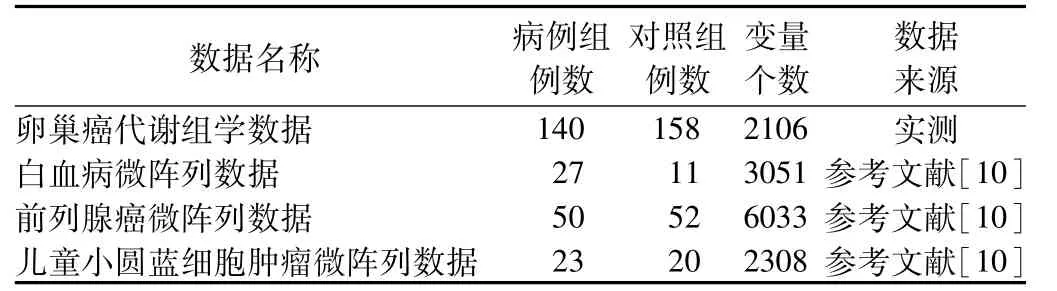
表1 四个数据集的相关信息

首先，将数据集进行标准化、归一化处理。然后分别利用PLS、RF、svmRFE进行变量筛选，计算SCSR的参数设置为e＝0.9，W＝100，保留排序靠前的0.5%、1%、2%、5%、10%、25%、50%的变量，分别计算 SCSR。结果表明:PLS方法筛选出变量的稳定性最好，其次是svmRFE方法，稳定性最差的是RF方法（图5）。

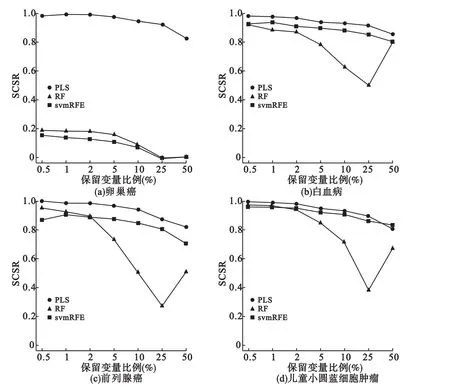
图5 不同数据集上三种变量筛选方法的SCSR值

讨 论

1.变量筛选方法的稳定性是指数据的轻微变动引起结果变化的情况。实际中，如果筛选出的变量具有很好的稳定性，则更有理由相信得到的结果具有较好的重现性，否则需要慎重对待得到的结果。

2.本文在简要介绍了六种稳定性评价指标的基础上，通过设置适当的条件和模拟实验分析对比了六种指标的性质。结果显示，KI、SCSR和RCW三种方法相对较好，特别是SCSR方法无论在准确性和稳定性上都具有更好的性质，是我们推荐使用的方法。

3.通过实例分析，利用SCSR在四种数据集上对PLS、RF、svmRFE三种变量筛选方法的稳定性进行了分析。结果显示，总体上PLS的稳定性最好，svmRFE次之，RF方法的稳定性最差。

4.从应用角度看，对于代谢组数据，无论取多少变量作为“差异变量”，使用svmRFE和RF方法筛选出的变量都不够可靠，PLS方法则显现出很好的稳定性，从中说明了为什么PLS方法在代谢组学中有着更广泛的应用。对于基因组表达数据，在取2%的变量作为“差异变量”时，三种方法筛选变量的稳定性相差并不大，也从另一方面说明，svmRFE和RF方法可能对“差异大小”更为敏感，很可能基因组表达数据中大概只有2%的基因是真正的差异基因，这与文献报道一致。

［1］Salem A，Zheng Z，Huan L.A Dilemma in Assessing Stability of Feature Selection Algorithms.International Conference on High Performance Computing and Communications Banff:IEEE，2011:701-707.

［2］Kevin D，Padraing C，Francisco A.Solutions to Instability Problems with Sequential W rapper-based Approaches to Feature Selection.Journal of Machine Learning Research，2002，2:748-769.

［3］M iron BK.Robustness of Random Forest-based gene selection methods.BMC bioinformatics，2014，15（1）:8-15.

［4］Kalousis A，Prados J，Hilario M.Stability of feature selection algorithms:a study on high-dimensional spaces.Know ledge and Information Systems，2007，12（1）:95-116.

［5］Kuncheva LI.A stability index for feature selection.IASTED International Multi-Conference:artificial intelligence and applications Innsbruck:IASTED，2007:390-395.

［6］Somol P，Jana N.Evaluating the Stability of Feature Selectors That Optimize Feature Subset Cardinality.Proceedings of the 2008 Joint IAPR International Workshop on Structural，Syntactic，and Statistical Pattern Recognition，2008:956-966.

［7］武海滨，张涛，赵发林，等.基于偏最小二乘线性判别分析的遗传算法在代谢组学特征筛选中的应用.中国卫生统计，2013，30（4）:517-520，524.

［8］武晓岩，李康.随机森林方法在基因表达数据分析中的应用及研究进展.中国卫生统计，2009，26（4）:437-440.

［9］武振宇，李康.支持向量机在基因表达数据分类中的应用研究.中国卫生统计，2007，24（1）:8-11.

［10］Uriarte R，Andres SA.Gene selection and classification of microarray data using random forest.BMC bioinformatics，2006，7（1）:3-15.

Theory and Application of Stability Measurement of Vaviable Selection Methods in High-dimensional Data

Wang Jingtao，Hou Yan，Li Kang（Department of Health Statistics，School of Public Health，Harbin Medical University（150086），Harbin）

ObjectiveIn the process of feature selection，the results of feature selection methods will be diffierent as instances vary slightly.Our research is to study how to measure the stability of the feature preference.MethodsWe perform simulation experiments to compare the accuracy and variation degree of six measurement of stability:HD，SCSR，TD，KI，CW，RCW．SCSR is further studied by applying PLS，RF，svmRFE to real data.ResultsWhen the feature preference is generated randomly，SCSR，KI，RCW are always close to them inimumnomatter the number of features remained.When we apply PLS，RF and svm-RFE to the data which labels and value of features is permutated and measure stability of results，the stabilities of PLS，RF and svmRFE are almost identical，and SCSR，KI，RCW are still close to them inimum no matter the number of features remained.In the terms of stability of measures themselves，the variation of HD and SCSR are small，this two measures have better robustness.ConclusionSCSR performs best in the terms of accuracy and variation degree，and is recommended by us as the measure of stability.

Omics；High-dimisional data；Feature selection；Stability

国家自然科学基金资助（81473072）

△通信作者:李康，E-mail:likang@ems.hrbmu.edu.cn

（责任编辑:郭海强）