基于MATLAB 和1stOpt 的非线性曲线拟合比较

孙立珍，赵乐乐

（内蒙古建筑职业技术学院信息网络中心，呼和浩特 010070）

0 引言

曲线拟合是数据分析和处理时重要的方法之一，根据变量之间关系的不同可分为线性曲线拟合和非线性曲线拟合两种[1]。线性曲线拟合通常是采用一组简单的、线性无关的基函数来逼近测量数据，进而求解参数，许多非线性曲线拟合问题也是经过函数的非线性变换转为线性拟合问题来处理[2]。非线性曲线拟合通常是基于MATLAB、Origin 和Maple 等数学软件利用最小二乘法或其他优化方法求解模型参数，文献[3-6]是基于MATLAB 进行曲线拟合，文献[7-9]是基于Origin进行曲线拟合，文献[10-11]是基于Maple 进行曲线拟合，这些软件在使用过程中经常遇到初值设定困难、收敛性差和精度低等问题。特别是参数初值的设定往往凭借经验进行试探，具有很大的盲目性，初值设定不当直接导致拟合无法收敛或局部最优的结果[12]。目前也存在像文献[13-14]用的 Lingo 和文献[15-16]用的1stOpt 不需要设定初值的数学软件，所有用于曲线拟合的软件各具特点。

本文以某一锂离子电池在放电结束后的端电压变化曲线为拟合对象，分别基于MATLAB、1stOpt 进行非线性拟合，从拟合精度和软件的易用性两个方面，对MATLAB 和1stOpt 这两种常用的数学软件所提供的曲线拟合方法进行对比分析。

1 非线性曲线拟合

非线性曲线拟合多指通过一组实验数据（xi，yi），（i=1，2，3，…，n），寻找一个y 与x 之间的函数f（x，y），使得xi 处的函数值在最小二乘准则下与观测值的偏差最小，让f（x，y）尽可能准确地表示出xi 和yi 两个被描述量之间的关系[17]。因此，对于在最小二乘准则下的非线性曲线拟合方法，可以通过残差平方和来比较分析其拟合效果。

目前，非线性曲线拟合问题比较普遍，可利用的软件也比较多，有需要进行参数初值设定的，也有不需要进行参数初值设定的，各种应用场景不甚相同。MATLAB是MathWorks 公司开发的商业数学软件，提供有lsqcurvefit（）和 lsqnonlin（）两个非线性曲线拟合函数，这两个函数采用同一种拟合算法，即最小二乘法。1stOpt是由七维高科有限公司开发的一套数学优化分析综合工具软件包，其核心算法是“通用全局优化算法（UGO）”，可用于非线性回归、曲线拟合和非线性复杂工程模型参数辨识等领域。

2 非线性拟合对比分析

本文通过锂离子电池放电结束后的二阶RC 等效电路的零输入响应对电池端电压测量值进行非线性拟合，辨识相关参数，对比分析MATLAB 和1stOpt 两种拟合方法易用性和精确性。锂离子电池放电结束后的二阶RC 等效电路的零输入响应表达式如式（1）所示[18]。

式中，UL表示电池的端电压，UOC表示电池结束放电后的开路电压，U1和U2分别表示两个RC 支路在放电结束时的电压，τ1和τ2分别表示两个RC 支路的时间常数，t 表示电池结束放电时长。

文献[19]对某一锂离子电池组进行脉冲放电，在其中一个脉冲放电后采集的端电压值如表1 所示，采样时间间隔为1s，共计20 个采样点。

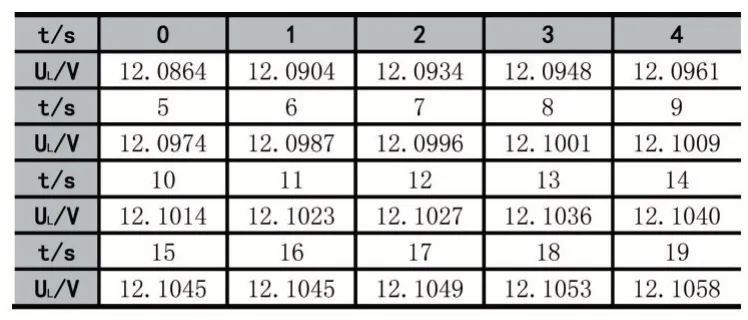
表1 采样时间和电池端电压

2.1 基于MAATTLLAABB的非线性曲线拟合

在已经获取了一组自变量和因变量数据的情况下进行非线性曲线拟合，可以直接使用lsqcurvefit（）函数，否则可以使用 lsqnonlin（）函数[20]。对于式（1）而言，在给定的输入数据t 和输出数据UL的情况下，基于MATLAB 建立可以表达电池放电结束后的二阶RC 等效电路的零输入响应的function，设定参数初值，利用lsqcurvefit（）函数实现最小二乘意义上的非线性曲线拟合，进而辨识参数 U1、τ1、U2和τ2。

当参数（U1，τ1，U2，τ2）的初值分别设定为（1，1，1，1）、（2，2，2，2）、（10，10，10，10）时，拟合曲线如图 1 所示，辨识的参数和拟合残差平方和（SSE）如表2。

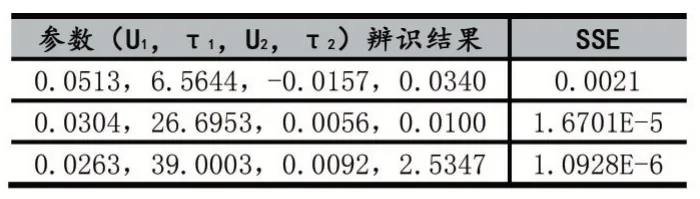
表2 辨识的参数和拟合残差平方和

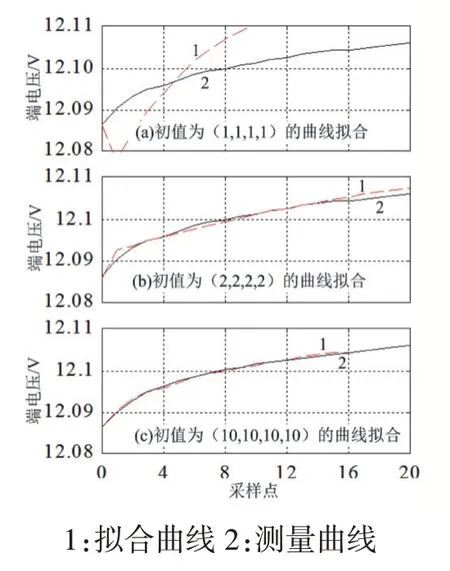
图1 电池端电压变化曲线

从以上拟合结果来看，当参数初值设定为（1，1，1，1）时，非线性曲线拟合无法收敛，且出现极化电压U2小于0 的现象，这与理论相悖；当参数初值设定为（2，2，2，2）时，虽然非线性曲线拟合可以收敛，SSE=1.6701E-5 较小，但仅是局部最优化，拟合度不高；当参数初值设定为（10，10，10，10）时，SSE=1.0928E-6 小于 1.6701E-5，非线性曲线拟合度提高，拟合结果接近全局最优。进而表明，基于MATLAB 进行非线性拟合会遇到参数初值设定困难的问题，特别是强非线性拟合，参数初值设定不当可能出现不能收敛或局部最优的现象。

2.2 基于1ssttOOpptt的非线性曲线拟合

1stOpt 的“UGO”可以解决目前在优化计算领域中使用迭代法所面临的初值设定难的问题，即参数初值不需要用户设定，代码执行时会随机给出，并通过其全局优化算法找出全局最优解，进而可以避免因初值选取不当而导致的局部最优或不能收敛的问题出现[21]。

基于1stOpt 定义参数和变量，建立锂离子电池放电结束后的二阶RC 等效电路的零输入响应的Function，优化算法选择“麦夸特法（LM）”，算法参数设定选择“标准LM+UGO”模式，执行代码可实现最小二乘意义上的非线性曲线拟合，不需要设定初值就可以辨识参数（U1，τ1，U2，τ2）。拟合曲线如图 2 所示，辨识的参数和拟合残差平方和如表3。

表3 辨识的参数和拟合残差平方和

图2 电池端电压变化曲线

基于1stOpt 的非线性拟合无需设定参数初值，代码编写简单，有多种可选的优化算法组合。从以上拟合结果来看，拟合精度较高，残差平方和为1.0926E-6，相对 MATLAB 在初值设定为（10，10，10，10）时的拟合残差平方和减小0.0183%，实现了全局最优化。

3 结语

对于非线性曲线拟合问题，数学软件MATLAB 和1stOpt 还是有较大区别的。MATLAB 虽然拟合速度较快，但需要设定参数初值，且要达到1stOpt 的拟合精度需要设定合适的参数初值，否则可能出现无法收敛或局部最优的问题。1stOpt 无需设定参数初值，利用“UGO”进行非线性拟合，拟合速度相比MATLAB 略低，但解决了目前在优化计算领域中使用迭代法所面临的初值设定难的问题，拟合残差平方和较小，精度较高，可以实现全局最优化。另外，利用1stOpt 进行非线性拟合时代码编写简单，默认输出迭代数、计算用时、残差平方和、均方差和相关系数等结果。