2004－2015年中国狂犬病发病数据ARIMA乘积季节模型的建立及预测

中国医科大学附属第一医院肿瘤所二室（110001） 孟凡东 吴 迪 隋承光

2004－2015年中国狂犬病发病数据ARIMA乘积季节模型的建立及预测

中国医科大学附属第一医院肿瘤所二室（110001） 孟凡东 吴 迪 隋承光

目的了解我国大陆地区2004－2015年狂犬病的发病情况，建立狂犬病发病的时间序列模型，利用模型进行短期预测，为狂犬病的预防和控制提供参考。方法通过查阅2004－2015年每月的《中华人民共和国卫生和计划生育委员会公报》，获得狂犬病发病的月统计数据，利用2004－2014年的数据建立ARIMA乘积季节模型，并利用建立的模型预测2015年数据，与实际发病数据比较。结果中国2004－2015年总计报告狂犬病25561例，年平均发病率为0.1592/10万，总计报告死亡病例22196例，年平均死亡率为0.1383/10万，2004年－2007年，狂犬病的发病人数和死亡人数逐年上升，2008年至2015年，持续下降。狂犬病具有一定的季节趋势，其中夏秋季节报告发病人数较多，而冬春季节发病人数较少。根据2004－2014年发病资料建立的最优时间序列模型为ARIMA（0，1，1）（0，1，1）12，模型预测2015年发病人数为764，相对误差7.73%。结论我国大陆地区狂犬病发病在2007年达到峰值之后，之后年发病率持续降低。ARIMA乘积季节模型能很好地拟合狂犬病发病的长期趋势和季节趋势，回代拟合和短期预测效果较理想。

时间序列 ARIMA乘积季节模型 狂犬病

狂犬病在世界范围内广泛存在，每年大约55000人死于狂犬病，其中95%的死亡病例发生在亚洲和非洲［1］。印度的狂犬病流行最为严重，中国紧随其后，列第二位［2］。在20世纪80年代前，中国每年有数千例患者感染狂犬病，严重威胁人们的生命健康。20世纪90年代，狂犬病的发病人数和死亡人数明显降低，1996年全年仅报告159例狂犬病感染病例［3－4］。随后，发病例数开始快速增加，2003年全国报告病例数超过2000例。

狂犬病由狂犬病病毒感染所致，可影响任何动物的中枢神经系统，但只在哺乳动物间传播流行［5］。感染者一旦发展到临床症状的出现，狂犬病几乎100%致死。因此，狂犬病的预防和控制非常关键。我国狂犬病病毒的携带者主要是家庭豢养的犬，并通过咬伤传染给人类［6］。在中国，随着经济的快速发展和家庭结构的改变，家养宠物狗的数量急剧上升，导致中国正面临狂犬病的爆发流行［7］。

本研究对2004－2015年中国狂犬病的发病进行描述性分析，并利用2004－2014年的逐月发病数据建立季节性时间序列模型，对2015年的发病情况进行预测。

资料与方法

狂犬病的月发病数据来自历年每月的《国家卫生和计划生育委员会公报》［8］，人口数据来自《中国卫生统计摘要》［9］。

求和自回归移动平均（autoregressive integrated moving average，ARIMA）［10］模型是时间序列分析方法中重要而基本的模型之一，它用特定的数学模型描述与时间相关的一组随机变量之间所具有的自相关性，以掌握预测对象的发展趋势，并根据已获得的时序资料对其未来进行短期预测。ARIMA乘积季节模型，即 ARIMA（p，d，q）（P，D，Q）S模型，是随机季节模型（stochastic seasonal model）与 ARIMA模型的结合，用于分析拟合不仅含有季节性成分，还混有非季节性成分的时间序列资料。其中p、q、d分别为模型非季节部分的自回归平均阶数、移动平均阶数、差分次数，P、Q、D分别为季节性自回归平均阶数、移动平均阶数、季节性差分次数，s为一个季节周期中观测值的个数。

ARIMA（p，d，q）（P，D，Q）S模型建模分析过程具体分3个阶段进行［11］:（1）模型参数的确定，利用自相关和偏自相关分析时间序列原始数据的随机性、平稳性和季节性，初步确定模型参数p、d、q及P、D、Q、s的取值；（2）模型参数的检验，首先采用Box-Ljung检验模型的白噪声，以判断模型的拟合优度，若有两个或两个以上的模型通过了Box-Ljung检验，则根据Akaike′s information Criterion（AIC），Schwarz′s Bayesian Criterion（BIC）选择最适合的模型参数；（3）预测应用，通过对比模型预测值与实际值的差值，评价模型预测的准确性。预测的相对误差按下式计算:

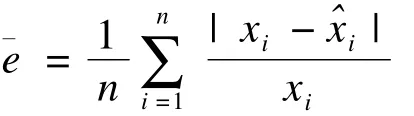
本研究中 ARIMA（p，d，q）（P，D，Q）S模型的建立、参数检验、预测均借助SPSS 13.0软件完成［12］。

结果与分析

1.狂犬病发病一般情况及其时间序列图

中国2004－2015年总计报告狂犬病25561例，年平均发病率为0.1592/10万，总计报告死亡病例22196例，年平均死亡率为0.1383/10万，各年情况见表1。2004－2007年，狂犬病的发病人数和死亡人数逐年上升，2008年至2015年，持续下降。

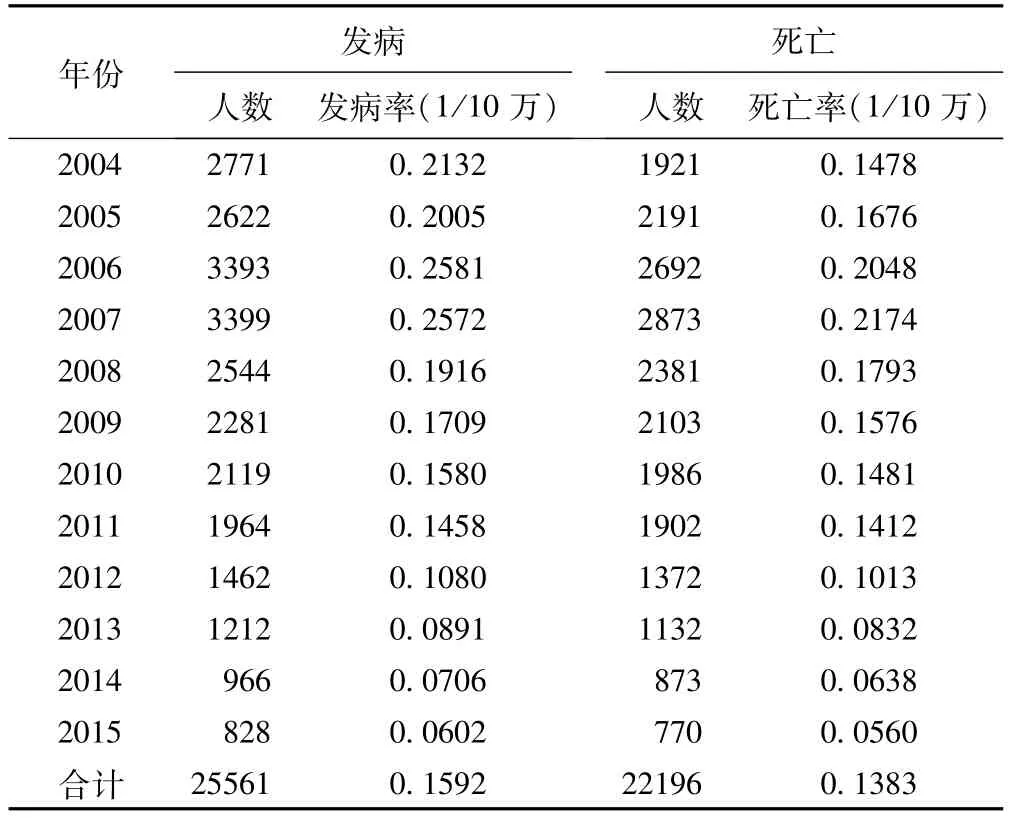
表1 2004－2015年中国狂犬病发病及死亡数据统计

从狂犬病的逐月发病人数看（表2），具有一定的季节趋势，其中夏秋季节发病人数较多，而冬春季节发病人数较少，历年季节趋势基本一致，见图1。

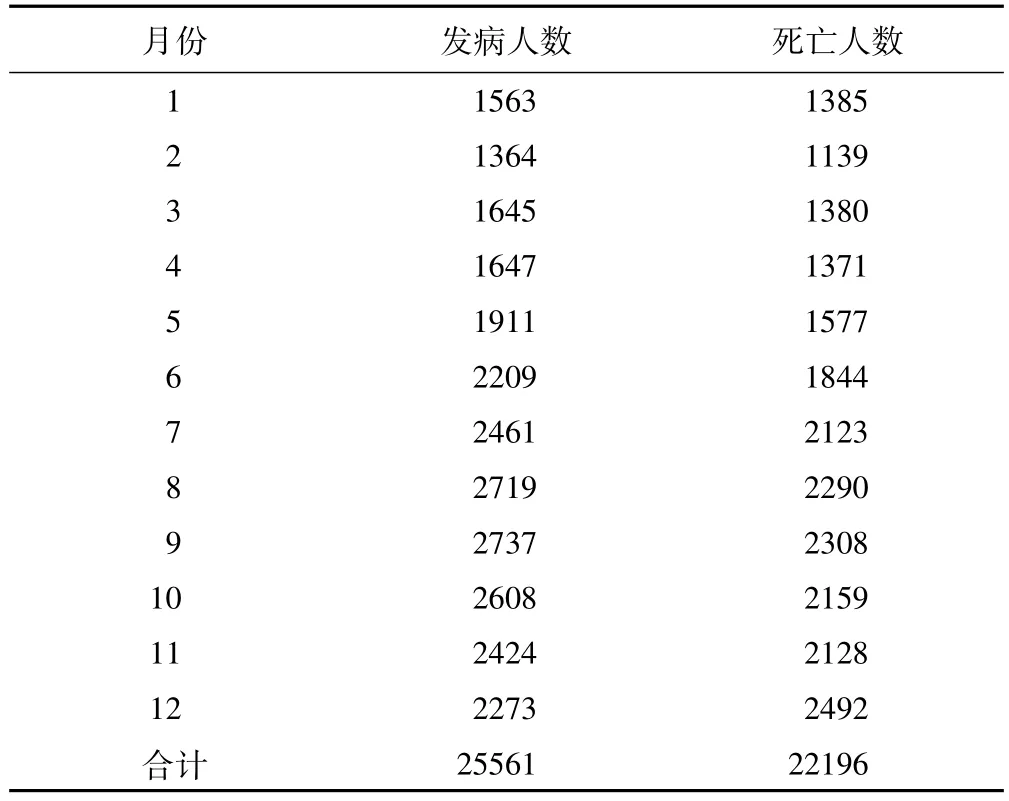
表2 2004－2015年按月统计中国狂犬病发病及死亡数

2.模型的识别与建立

以2004－2014年全国狂犬病报告发病数据构建ARIMA乘积季节模型。从图1狂犬病发病数据的原始序列图可见，狂犬病的发病数以年为周期的变化较明显。2004－2007年，发病数逐年上升，2008－2014年发病数逐年减少。为获得平稳的序列，先对原始数据进行自然对数转换，再分别进行一阶普通差分和一阶季节性差分，获得的序列见图2。对数转换和差分后序列的长期趋势和季节性趋势基本消失，数值围绕0上下随机波动，可进一步进行ARIMA模型建模分析。初步判断模型是以1年（12个月）为周期的季节乘积 ARIMA模型:ARIMA（p，1，q）（P，1，Q）12，待定参数p，q为连续模型部分的自回归阶数和移动平均阶数，P，Q为季节模型部分的自回归阶数和移动平均阶数。对于四个待定参数p，q，P，Q的确定，通常采用从低阶到高阶逐个尝试，通过比较各个模型的拟合优度确定。一般情况下，超过2阶的情况很少见。因此，本研究在确定d＝1，D＝1后，分别测试了在d＝1，D＝1的情况下，p，q，P，Q分别取 0，1，2的所有模型，共测试81个模型，综合考虑模型的残差白噪声检验（Box-Ljung test）结果，模型参数的检验结果，模型的AIC、BIC等，得到的最优模型为 ARIMA（0，1，1）（0，1，1）12。模型的参数估计结果见表3。模型残差的Box-Ljung检验P＞0.05。

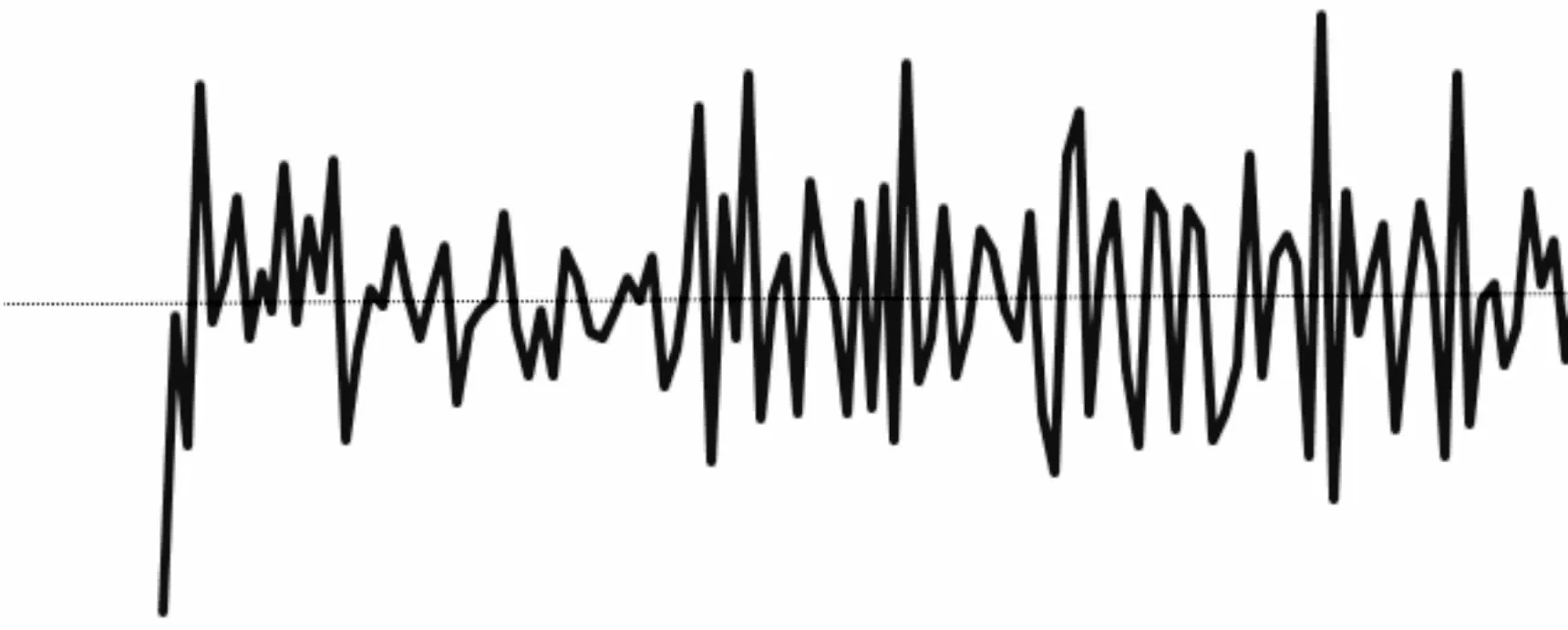
图2 2004－2014年狂犬病发病数经对数转换和一阶普通差分、一阶季节差分后的序列图

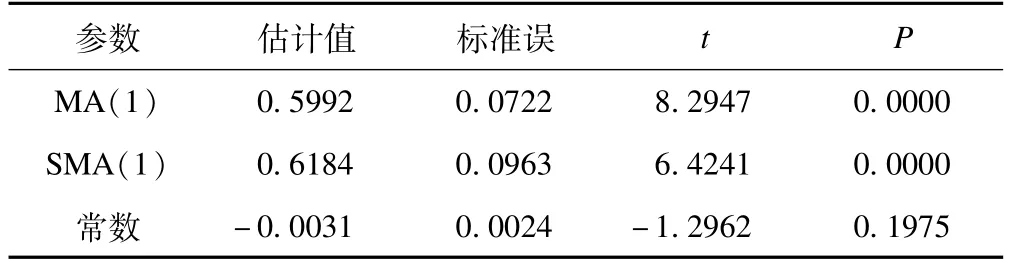
表3 最优模型 ARIMA（0，1，1）（0，1，1）12参数估计结果

3.模型的验证

（1）回代拟合 通过获得的最优模型ARIMA（0，1，1）（0，1，1）12对2004－2014年的发病数进行回代拟合，结果如图3所示，拟合值和实际值基本吻合，119对数据的平均拟合误差为11.21%。

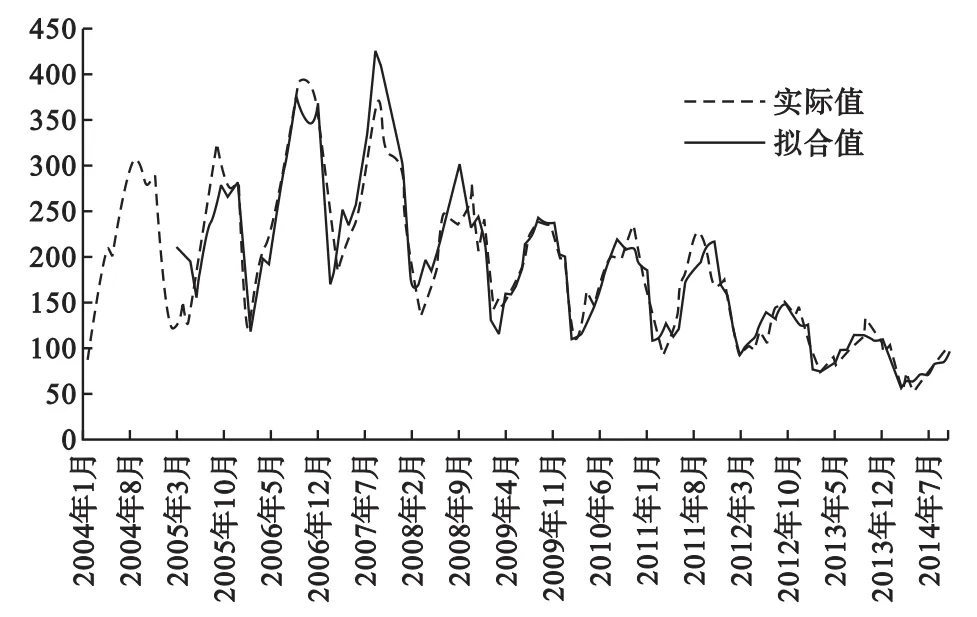
图3 模型 ARIMA（0，1，1）（0，1，1）12回代拟合比较

（2）预测利用建立的模型对中国2015年狂犬病的发病数进行预测，结果见表4。预测结果12个月的平均相对误差为14.19%，按全年发病例数计，相对误差为7.73%。

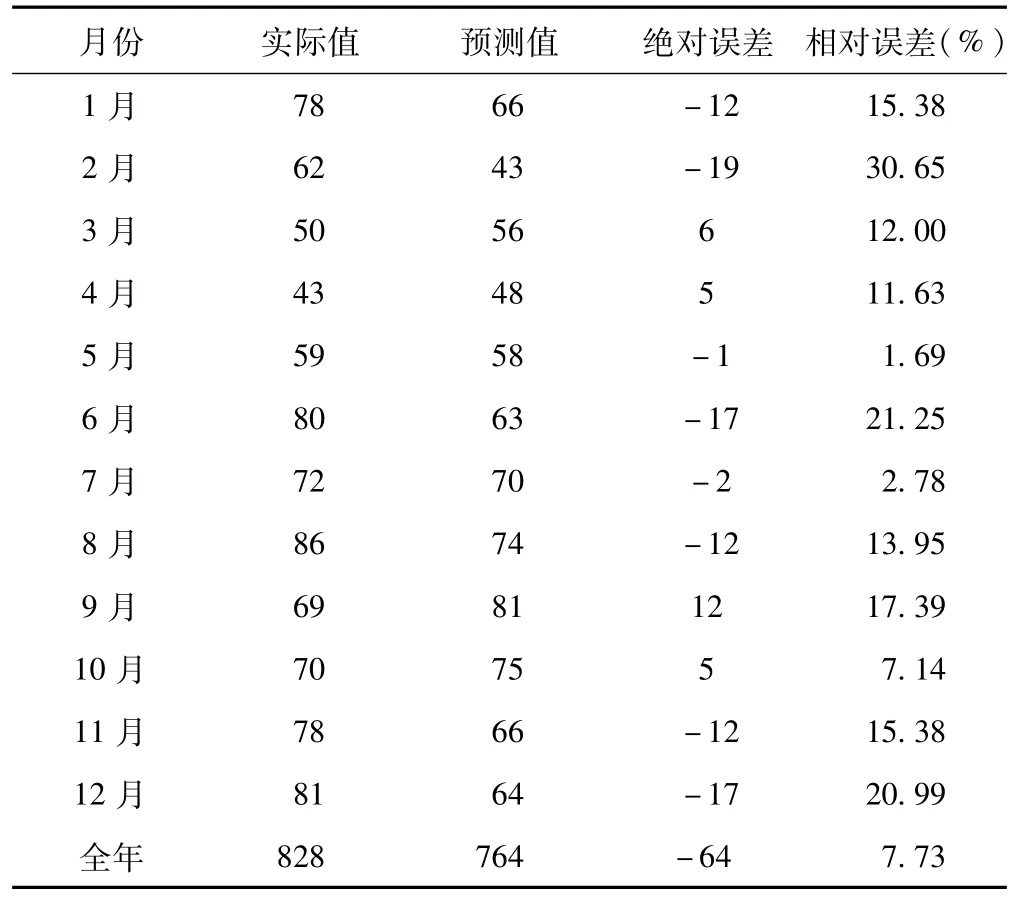
表4 模型 ARIMA（0，1，1）（0，1，1）12预测2015年狂犬病发病结果

讨 论

迄今为止，狂犬病的病死率几近100%，是人类病死率最高的急性传染病，而我国又是全球狂犬病流行最严重的国家之一，年报告发病数仅次于印度［13］。因此，狂犬病的疫情监测和预防控制，仍是我国传染病防制工作的重中之重。本研究应用ARIMA乘积季节模型分析了中国狂犬病2004－2015年的发病情况，原始数据来自国家卫生行政部分的疫情公报。目的在于找出近年狂犬病的流行特点，并对今后短期的流行做出预测。影响狂犬病流行的因素很多，预测模型往往很难将所有的影响因素纳入。在时间序列分析中，认为其他影响因素均包含在时间因子中，将时间因素作为一个综合影响因子进行模型的拟合与预测［14］。

利用2004－2014年中国狂犬病发病数资料，构建ARIMA乘积季节模型，最终选择 ARIMA（0，1，1）（0，1，1）12模型。该模型残差的白噪声检验、模型参数检验、拟合优度检验均有统计学意义，模型的回代拟合效果和预测效果均可接受。由于时间序列预测法所需要的只是序列本身的历史数据，因此，这一类方法在资料收集上的成本很低，有着宽广的应用前景。但与一般时间序列模型相比，ARIMA乘积季节模型需要更多的历史数据，模型确定中的难点是寻找对序列进行平稳性处理的方法，以提高预测模型的精度［15］。

对暴露人群进行预防处置（postexposure prophylaxis，PEP）和疫情监测是控制狂犬病的主要措施［15］。PEP主要包括暴露后及时规范地进行伤口处理、疫苗接种与抗狂犬病血清或人狂犬病免疫球蛋白注射。这些措施的实施通常受社会经济条件的影响，尽管中国的社会经济不断发展，在中国，特别是广大农村地区，被犬类的动物咬伤后接受PEP处理的比例仍相对较低。一项调查显示，2003－2004年，广东省被犬类等咬伤的居民中32.8%进行了暴露后预防处理，其中只有37.5%的人是到当地医院或疾病预防控制机构进行正确的伤口处理和预防。降低狂犬病疫苗的接种价格，提高人们对狂犬病的认知，是提升PEP比例、预防和控制人感染狂犬病的关键。

［1］Knobel DL，Cleaveland S，Coleman PG，et al.Re-evaluating the burden of rabies in Africa and Asia.Bull World Health Organ，2005，83:360-368.

［2］郭绶衡，唐青，李浩，等.中国31省1991－2005年狂犬病流行情况比较分析.中华流行病学杂志，2007，28（4）:374-376.

［3］唐青，赵秀芹，陶晓霞.中国人间狂犬病流行近况分析.中华流行病学杂志，2001，22（1）:8-10.

［4］Zhang YZ，Xiong CL，Xiao DL，et al.Human Rabies in China.Emerg Infect Dis，2005，11:1983-1984.

［5］Bourhy H，Dautry-Varsat A，Hotez PJ，et al.Rabies，Still Neglected after 125 Years of Vaccination.PLoSNegl Trop Dis，2010，4:e839.

［6］Song M，Tang Q，Wang DM，et al.Epidemiological investigations of human rabies in China.BMC Infect Dis，2009，9:210-219.

［7］Wu XF，Hu RL，Zhang YZ，et al.Reemerging Rabies and Lack of System ic Surveillance in People′s Republic of China.Emerg Infect Dis，2009，15:1159-1164.

［8］卫生部.2004－2015中华人民共和国卫生部公报.http://www.moh.gov.cn/publicfiles/business/htmlfiles/mohbgt/pggtg/index.htm.

［9］国家卫生计生委.2014年中国卫生统计提要.http://www.moh.gov.cn/publicfiles//business/htmlfiles/zwgkzt/ptjty/digest2010/index.html.

［10］Box GEP，Jenkins GM.Time Series Analysis:Forecasting and Control.2nd ed.San Francisco:Holden-Day，1976.

［11］郭海强，丁海龙，曲波，等.应用ARIMA模型对全国2004－2009年肾综合征出血热疫情分析及预测.中国人兽共患病学报，2010，26（12）:1137-1140.

［12］宇传华.SPSS与统计分析.第2版.北京:电子工业出版社，2014，645-679.

［13］李放湘.我国狂犬病流行与防制近况.医学动物防制，2012，28（4）:394-396.

［14］徐国祥.胡清友.统计预测和决策.上海:上海财经大学出版社，1998:150-275.

［15］卫生部，卫疾控发.狂犬病暴露预防处置工作规范（2009年版）.（2009－12－17）.http://www.moh.gov.cn/publicfiles/business/htmlfiles/mohbgt/s10695/200912/45090.htm.

Human Rabies Incidence in China:Trends and Predictions from a Time Series Analysis from 2004 Through 2015

Meng Fandong，Wu Di，Sui Chengguang.（The first hospital of China Medical University 110001，Shenyang）

Objectivewith an increasing population of dogs and low vaccination coverage，rabies is remerging and becoming a serious public health problem in China.Control and prevention of rabies requires know ledge of recent and future incidence trends.MethodsMonthly information on the incidence of human rabies from January 2004 through December 2015 was collected from the Gazette of the Ministry of Health of the People′s Republic of China.Autoregressive integrated moving average（ARIMA）multiple seasonal models were established to fit and predict rabies incidence using these data.The dataset was divided into two parts:data reported from January 2004 to December 2014，which were used to develop the time series model，and data from 2015，which were used to validate the established model.ResultsHuman rabies remains a serious infectious disease in China.During the 12 years that this study investigated，25561 rabies cases were reported in China.The annual average number of cases was 2 130 and the incidence was 0.1592/105people.The seasonal ARIMA（0，1，1）（0，1，1）12model was the best to fit the data from the year 2004 to 2014.Using this model，we predicted 764 rabies cases in all of China in 2015.The actual number of reported cases was higher than the prediction for all of 2015（828 vs.764），for a relative predictive error of7.73%，which was statistically acceptable.Conclusionthe number of rabies cases reported reached its peak in the year of 2007，then it has been show ing a downward trend since then.The seasonal ARIMA（0，1，1）（0，1，1）12model was significant，with an acceptable estimative and predictive accuracy.The time series model can be used to analyze and predict rabies cases in China，and w ill help frame strategies to control and prevent the disease.

Time series；The seasonal ARIMA；Human rabies

（责任编辑:郭海强）