数学核心素养的内涵与构成分析

2016-12-22孙月霞

初中生世界 2016年48期

■孙月霞

数学核心素养的内涵与构成分析

■孙月霞

数学素养是通过数学学习所获得的提出、分析与解决问题的能力，随着新课程改革不断深入，数学核心素养的培养越来越受到社会的重视。本文从数学核心素养的特点和构成、数学核心素质与数学思想方法等概念的关系进行了分析，力求探讨数学核心素养的实质，进而在数学教学过程中不断提高教学质量和效率，增强学生的数学素养和能力。

数学核心素养特点构成相互关系

一、数学核心素养的特点

1．具有层次性和连续性。

在学生学习不同层次的数学时，数学核心素养的培养内容也是不同的，但是各个层次之间，数学核心素质的培养是具有连续性的。从纵向来看，学生数学核心素养的形成是不断递进的；从横向来看，随着学生不断地学习和能力的提升，自身的数学核心素养也会有差异。比如，在小学时期，注重运算、归纳等能力的培养，在中学时期，注重逻辑等能力的培养，在不同的学习层次，学生学习的数学知识和技能不断变化，数学核心素养也不断完备。

2．具有抽象性和场景性。

数学核心素养的养成需要一个长期的过程，不像具体的数学知识可以短时间获得。数学本真来源于现实生活，在进行数学核心素养培养时，要回归社会生活。比如在小学、中学阶段，学生的数学整体素养还比较低，对数学抽象类的概念和知识理解不到位，这就需要利用现实、直接和形象的场景去引导学生对数学知识的学习，数学核心素质的培养需要数学知识的场景化进行支撑。

3．具有综合性和感悟性。

数学核心素养是学生在数学知识、技能、态度和思考等方面的综合性体现，形成于学生数学学习的各层次和各阶段。通常情况下，基本的数学知识和技能，在教师的讲解和传授以及平时的训练中可以获得，然而对于数学态度、思考等方面是不能直接传授的，需要学生在数学学习的过程中去感悟和领会。

二、数学核心素养的构成

1．数学抽象。

题目:某超市打出优惠牌子，上面说：购买茶壶、茶杯可以有两种优惠方法:（1）是买一送一（即买一只茶壶送一只茶杯）,（2）是打九折（即按购买总价的90%付款），假定每只茶壶20元，每只茶杯5元,假定某顾客要买4只茶壶，那么买几只杯子最合算呢？

解：当然杯子不少于4只。设买茶杯x只付款y元，x＞3，且x为自然数。

用第一种方法付款：y1=4×20+（x-4）×5=5x+ 60；用第二种方法付款：y2=（20×4+5x）×90%= 4.5x+72。设d=y1-y2=5x+60-（4.5x+72）=0.5x-12。然后进行讨论：

①当d＞0时，0.5x＞12，即x＞24；②当d=0时，x=24；③当d＜0时，3＜x＜24.

上述题需要利用数学抽象思维抓住题目的本质。数学抽象作为数学基础思想之一，存在于数学发展的整个过程中，是理性思维形成的基础。数学抽象就是放弃事物的外在具体的物理特征，将问题提升到数学层面研究的思维过程。例如对现实生活中自由落体等现象抽象出函数，对立体几何抽象出了以公共点个数进行区分的线面的关系等等，所以要加强学生抽象思维的锻炼。

2．逻辑推理。

例题：已知一元二次方程的两根为-3和5，求二次项系数为2的一元二次方程。

解：设该一元二次方程为2x2+bx+c=0；

∵该方程的两根为-3和5，

∴将根代入，解得b=-4，c=-30；

∴所求的一元二次方程为2x2-4x-30=0。

上述解题的过程就体现了逻辑推理，逻辑推理是数学重要素养的组成部分。逻辑推理是对某些事实和命题按照逻辑规则进行推理的思维过程，一般分为两类，从一般到特殊以及从特殊到一般，采用归纳、类比和演绎等推理方式。通过逻辑思维素养的培养，促进学生比较、分析等能力的发展，进一步养成有序、严密的思维方式。

3．数学建模。

数学建模就是针对抽象的数学问题，采取假设、建模、求解和验证等相关步骤，让抽象的数学问题贴近现实的需要。对学生来说在进行数学建模的过程中，也是一个创新、探索和提高的过程。例如解三角形、不等式以及存储、分期付款等实际问题，都涉及数学建模，这就需要教师平时注重学生创新意识的培养，提高学生数学核心素质。

4．数学运算。

数学运算能力是数学最基本的能力，主要是利用运算法则对数学对象进行运算的过程，数学运算主要涉及到运算对象、运算法则、运算过程以及运算结果等多个方面，通过学习和掌握数学运算，可以帮助学生利用数学运算解决现实的问题，提高学生的数学思维能力，其中特别重要的是形成严谨、科学、有序的思考方式和方法。

5．直观想象。

题目:已知在三角形ABC中，D为BC边上的中点，在AD上任取一点E，连接BE，延长BE交AC于F，BE=AC，求证AF=EF．

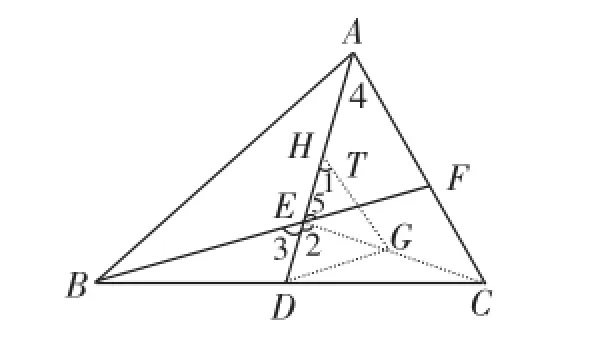
证明:如图，连接EC，取EC的中点G，AE的中点H，分别连接DG，HG。则:GH=DG。所以:∠1=∠2，而∠1=∠4，∠2=∠3=∠5。所以∠4=∠5，所以AF=EF。

上述题目需要充分发挥直观想象力。直观想象是进行抽象、逻辑推理的重要基础，对提出、分析和解决数学问题至关重要。直观想象就是通过几何感知和空间想象，对图形和数学问题进行解决的过程，主要涉及空间事物关系、运动规律以及图形等。加强对直观想象素养的培养，能够促进学生几何和空间想象能力的提升，强化其数形结合解决数学问题的能力，推动学生创新。