具有二阶矩有限噪声的Lasso高维统计分析

董青

（西北大学数学学院，陕西西安710127）

具有二阶矩有限噪声的Lasso高维统计分析

董青

（西北大学数学学院，陕西西安710127）

研究在非高斯噪声下的Lasso的高维统计分析，给出了在误差噪声满足二阶矩有限条件下，Lasso方法的高维界估计，推广了现有的关于Lasso的主要理论结果.所得结果具有一定的理论及应用价值.

Lasso；稀疏；高维数据

1 引言

高维数据处理是机器学习和统计学等领域的研究热点之一.而高维特征是海量数据的一个重要特征，其特点在于所研究问题的未知参数的维数远远大于所观测到数据的个数.显然，此问题对应于一个病态问题，问题的求解依赖于额外的信息.近20年来，在统计学以及信息信号处理等领域均开展了关于此问题的研究，代表性的工作包括Tibshirani在1996年提出的Lasso［1］.以及信号重建方面的压缩感知方向的诸如Candes和Donoho［24］等工作，即所谓的L1正则化方法.此方面的开创性工作为高维数据分析提供了有力的工具，也为近年来机器学习和统计学研究提供了基础.自L1正则化方法提出后，大批学者开展了关于其理论及算法的研究工作，比较有影响的工作有文献［28］.上述主要的理论结果均在误差是高斯噪声的假设下，而在实际工作中，存在多种噪声形式.因此开展在非高斯噪声下的L1正则化方法的高维统计分析有着非常重要的理论及应用价值.

本文开展此方面的工作，利用新的不等式，在误差噪声满足二阶矩有限的条件下，研究L1正则化方法的高维统计性质.

2 非高斯噪声下的L1正则化

下面给出在上述假设下L1正则化的理论分析.

定理2给出了Lasso在二阶矩有限条件下的高维统计分析.从不等式右端可以看出，界通过样本数n、参数维数p以及变量的稀疏度K给出，即所谓的高维性质.

3 实验结果

本节通过实验验证本文所给理论的正确性.在本实验中，线性模型（1）假设噪声服从［0，1］上的均匀分布，其中真实

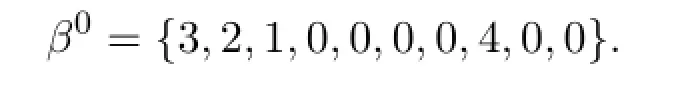
调用Matlab中的Lars程序，所得结果的路径如下图所示.参数λ的选择利用了10倍交叉验证，所得结果

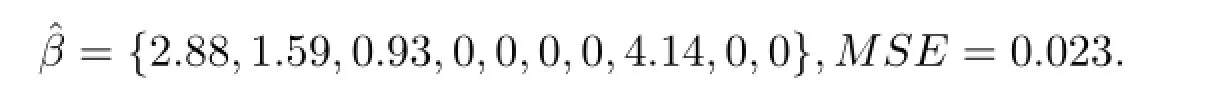
可以看出，对有界噪声，Lasso可准确选择出正确的模型.从而佐证了本文所给理论的正确性.

图1 Lasso变量选择结果

4 结论

L1正则化是近年来处理高维数据的有力工具，本文关注非高斯噪声的L1正则化的理论性质分析.在噪声满足二阶矩有限条件下给出了L1正则化的解的统计性质分析.近年来，L1正则化方法被推广到多方面的问题研究，例如文献［9-10］所做的工作.本文工作可推广到此类问题的研究.

［1］Tibshirani R.Regression shrinkage and selection via the lasso［J］.Journal of the Royal Statistical Society：Series B，1996，58：267-288.

［2］Candes E，Tao T.The dantzig selector statistical estimation when p is much larger than n［J］.Annals of Statistics，2007，35：2313-2351.

［3］Chen S，Donoho D，Saunders M.Atomic decomposition by basis pursuit［J］.SIAM Journal on Scientific Computing，1998，43：33-61.

［4］Donoho D.Compressed sensing［J］.IEEE Transaction on Information Theory，2006，54（4）：1289-1306.

［5］Zhao P，Yu B.On model selection consistency of Lasso［J］.Journal of Machine Learning Research，2006，7：2541-2563.

［6］Efron B，Hastie T，Johnstone L，et al.Least angle regression［J］.Annals of Statistics，2004，32（2）：407-499.

［7］Bühlmann P，van de Geer S.Statistics for High-dimensional Data：Methods，Theory and Applications［M］. New York：Springer，2011.

［8］Wainwright M.Sharp thresholds for high-dimensional and noisy sparsity recovery using l1-constrained quadratic programming（Lasso）［J］.IEEE Transaction on Information Theory，2009，55：2183-2202.

［9］Yuan M，Lin Y.Model selection and estimation in regression with grouped variables［J］.Journal of the Royal Statistical Society：Series B，2006，68（1）：49-67.

［10］Zou H，Hastie T.Regularization and variable selection via the elastic net［J］.Journal of the Royal Statistical Society：Series B，2005，67：301-320.

The high dimensional statistical analysis of Lasso with second moment noise

Dong Qing
（School of Mathematics，Northwest University，Xi′an710127，China）

In this paper，we study the high-dimensional statistical theory of Lasso with the bounded second moment noise.We propose the nonasymptotic bounds of Lasso which generalize the existing results.The results are of great theoretical importance and applied value.

Lasso，sparse，high-dimensional data

O236；O213

A

1008-5513（2016）02-0206-06

10.3969/j.issn.1008-5513.2016.02.012

2015-12-28.

国家自然科学基金（11571011）.

董青（1990-），硕士生，研究方向：统计机器学习.

2010 MSC:39A05，34B10