域上两类矩阵保逆的诱导映射

闫盼盼，曹重光

（黑龙江大学数学科学学院，黑龙江哈尔滨150080）

域上两类矩阵保逆的诱导映射

闫盼盼，曹重光

（黑龙江大学数学科学学院，黑龙江哈尔滨150080）

令F是一个域，Sn（F）是F上所有n×n上对称矩阵的集合.用Tn（F）记F上所有n阶上三角阵的集合.首先分别给出诱导映射和保逆性的定义.然后改进了关于复对称阵保逆的主要相关结果及其证明，得到了Sn（F）保逆诱导映射的一般形式，最后借助于类序列技术和初等方法刻画了Tn（F）保逆诱导映射.它推广和改进了带有附加条件（fij（x）=0⇔x=0）的相关结果.

域；对称矩阵；上三角矩阵；保逆；诱导映射

1 引言

关于矩阵保持问题研究，近年来更感兴趣于刻画没有线性和加法假定的保持映射，例如文献［1-7］.本文研究的诱导映射也属于这个方向.

设F是一个域，Mn（F）及Sn（F）分别记F上所有n阶矩阵及所有n阶上对称矩阵的集合，用Tn（F）

记F上所有n阶上三角阵的集合.设f是Mn（F）（Sn（F），Tn（F））到自身的映射，fij是F上的函数，其中ij∈｛1，2，···n｝.如果定义

则称f是由｛fij｝诱导的映射.简称Mn（F）（Sn（F），Tn（F））的诱导映射.

如果AB=In意味着f（A）f（B）=In，则f被称为保逆矩阵.关于方阵的保逆矩阵的诱导映射的刻画由文献［1］完成.之后，文献［5］给出了复数域上对称阵保逆诱导映射的一般形式，文献［6］在一定条件下给出了上三角矩阵保逆诱导映射的刻画.本文试图将文献［5-6］的结果推广到一般域上，同时将去掉文献［6］的条件（ChF/=2，fij（x）=0⇔x=0），得到完整的刻画.

在本文中用F∗记F中所有非0元的集合，Eij表示（i，j）位置是1，其余位置是零的矩阵，In记n阶单位阵.A⊕B表示矩阵A与B的直和，［1，n］表示集合［1，2，···，n］.

2 对称矩阵保逆的诱导映射

定理2.1 设F是一个域，n为整数且n≥3，f：Sn（F）→Sn（F），是由｛fij｝诱导的映射，且f（0）=0.则f是保逆的充分必要条件是；存在对合对角矩阵P及ε=±1，使得对于任意A∈Sn（F），有f（A）=εPAδP，其中δ是域上的单自同态，Aδ=（δ（aij））.

3 上三角矩阵保逆的诱导映射

现在对Tn（F）的诱导映射定义中涉及到的函数f12，f23，···，fn-1，n，定义类集合：

将函数f12，f23，···，fn-1，n所属的类集合，从左到右依次写成一个序列，称为f的类序列.例如ητρρητ为n=7时f的类序列，它说明f12∈η，f23∈τ，f34∈ρ，f45∈ρ，f56∈η，f67∈τ.

引理3.1 设n≥3是整数，f（0）=0，其中f是Tn（F）的保逆的诱导映射，则在f的类序列中不会出现相邻两类为ρτ，τρ，ττ这三种情况.

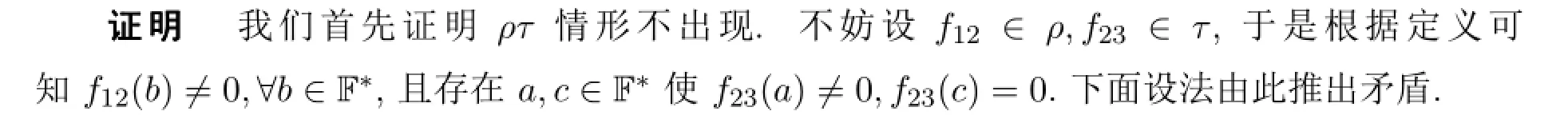
定理3.2 设f为Tn（F）的诱导映射，f（0）=0，n≥3是一个整数，则f保逆当且仅当

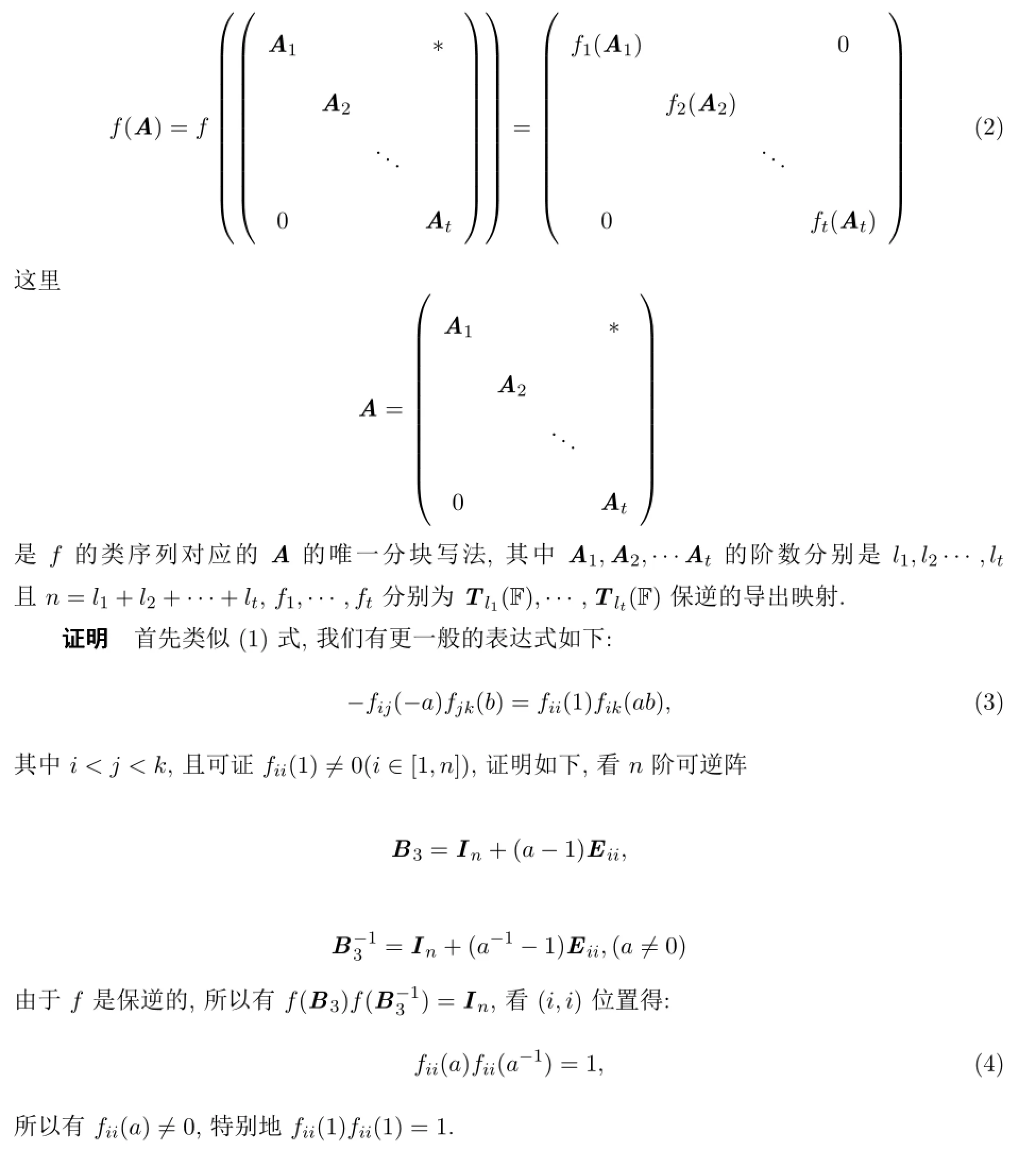
定理3.3 设F为任意域，n为整数且n≥3，f1为Tm（F）的诱导映射，f1（0）=0，

［1］Yang L，Ben X Z，Zhang M，et al.Induced Maps on matrices over fields［J］.Abstract and Applied Analysis，2014，2014（27）：1-5.

［2］Cao C G，Ge Y L，Yao H M.Maps preserving classical adjoint of products of two matrices［J］.Linear and Multilinear Algebra，2013，61（12）：1593-1604.

［3］Huang LP.Geometry of Matrices over Ring［M］.Beijing：Science Press，2006.

［4］You H，Wang Z Y.k-Potence preserving maps without the linearty and surjectivity assumptions［J］.Linear Algebra Appl，2007，426：238-254.

［5］吴丹，李贺，曹重光.域上对称矩阵保逆的导出映射［J］.高师理科学刊，2015，35（8）：1-3.

［6］吴丹，李贺.上三角矩阵保逆的诱导映射［J］.哈尔滨理工大学学报，2015，20（5）：116-118.

［7］张隽，付丽，曹重光.保体上上三角幂等矩阵的诱导映射［J］.纯粹数学与应用数学，2015，31（6）：628-635.

Induced maps preserving inveres of two kinds of matrices over fields

Yan Panpan，Cao Chongguang
（School of Mathematical Science，Heilongjiang University，Harbin150080，China）

Supposed that F is a field and n≥3 is an integer.Denote bySn（F）the set of all n×n symmetric matrices over F，Tn（F）the set of all n×n upper triangular matrices over F.First，the paper gives the definition of induced map and preserving inveres，respectively.And then，proof of main result about preserving inveres on symmetric matrices is improved，the general forms of induced maps preserving inverses on Sn（F）is obtained.Finally，induced maps preserving inveres on Tn（F）is characterized by class-sequence technigues and elementary methods，which generalize and improve relevant results with strings attached（fij（x）=0⇔x=0）.

field，symmetric matrix，upper triangular matrix，preserving inveres，induced map

O152.5

A

1008-5513（2016）02-0149-11

10.3969/j.issn.1008-5513.2016.02.006

2016-01-02.

国家自然科学基金（11371109）.

闫盼盼（1990-），硕士生，研究方向：矩阵代数.

2010 MSC:15A04