包含k-树图的毁裂度条件

李红燕

（青海民族大学数学院，青海西宁810007）

包含k-树图的毁裂度条件

李红燕

（青海民族大学数学院，青海西宁810007）

连通图G的一个k-树是指图G的一个最大度至多是k的生成树.对于连通图G来说，其毁裂度定义为

毁裂度；k-树；导出子图

1 引言

本文只考虑无环无重边的有限无向图.设图G=（V，E）是一个简单连通图，其顶点集为V（G），边集为E（G）.用∆表示图G的最大度，并且用G［S］定义由图G的一个顶点集V（G）的子集S导出的子图.我们用dG（v）表示图G中一个顶点v的度，并且用NG（v）表示与顶点v邻接的点的集合.对图G的顶点集V（G）的一个非空子集S，有

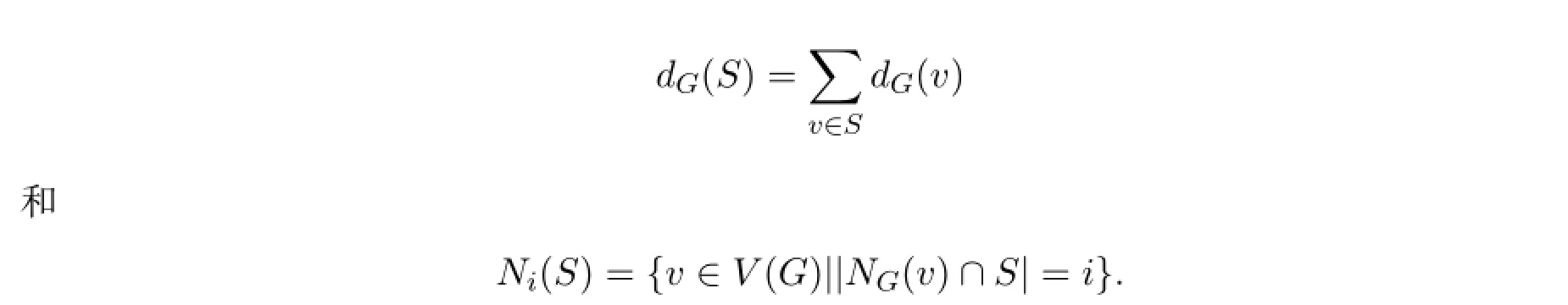
连通图G的一个k-树是指图G的一个最大度不超过k的生成树.显然，如果k=2，它就是图G的一个哈密顿路；由于每一个最大度为∆的树都有一个∆-树，因此本文中连通图G不再考虑树.

设S是图G的一个非空的独立的顶点集.如果对S的任意一个子集S′都能使G-S′连通，则称S是图G的一个框架.如果|S|=k，则称S为一个k-框架.

在文献［1，2］中，作者给出了图G包含一个k-树的Ore型与Fan型条件，具体如下：

定理1.1 如果G的每一个具有k个顶点的独立集S都满足：dG（S）≥n-1，则G是一个k-树.

2013年文献［3］中给出了一个关于k-树的更强的结论，就是下面的定理1.3.

定理1.3 设G是连通图并且k（≥2）是一个整数.如果对G中的每一个k+1-框架S，都有

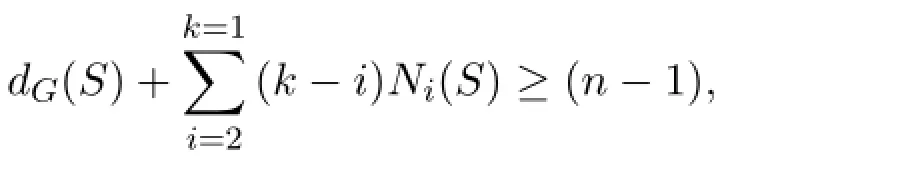
则G包含一个k-树.

文献［4］中介绍的图G的毁裂度是一个衡量连通图G的结构特征的重要参数，它具体定义如下：

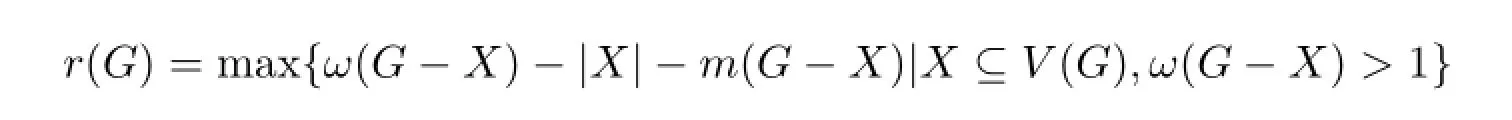
其中ω（G-X）和m（G-X）分别表示G-X中的分支数目和最大分支的阶数.

本文中，考虑一个连通图G中的毁裂度和k-树的存在性的关系，给出了一个图有k-树的新的充分条件.

2 主要结论

设G是一个连通图，k是一个整数并且2≤k≤∆.现在，通过证明下面的定理来讨论图G的毁裂度与图G的k-树的存在性之间的关系.

定理2.1 设G（不是树）是一个连通图，如果对G的任意一个点割集X，若

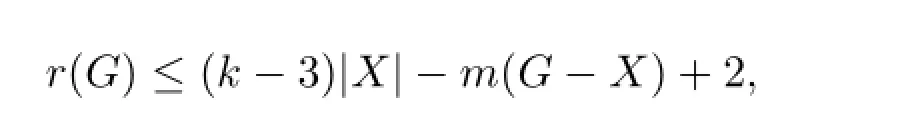
则G包含k-树.

首先设H是图G包含k-树的所有导出子图中阶数最大的子图之一，A表示子图H中与V（H）之外点相邻的点集.显然，若A=∅，则G包含k-树.现在假设对于图G的任一点割集X⊂V（G）来说有

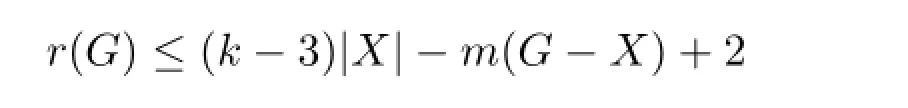
且A是非空的.下面通过反证法证明以上定理.首先证明几个有用的引理.

［1］Li Y，Zhang S，Li X.The rupture degree of graphs［J］.International journal of computer mathematics，2005，82（7）：793-803.

［2］李银奎，段宝荣，陈忠.完全k叉树的离散数与完整度［J］.纯粹数学与应用数学，2011，27（3）：1-7.

［3］李银奎，陈忠.完全k叉树的粘连度［J］.纯粹数学与应用数学，2013，29（5）：28-34.

［4］武燕，魏暹荪.关于图的边粘连度［J］.工程数学学报，2004，21（5）：34-39.

［5］魏暹荪.图论基础［M］.西安：陕西师范大学出版社，1991.

［6］Bagga K S，Beineke L W，Lipman M I，et al.Edge-integrity：asurvey［J］.Discrete Math.，1949，124：3-12.

［7］Piazzal B L，Roberts F S，Stueckle S K.Edge-tenacious networks［J］.Networks，1995，25：7-17.

The condition of rupture degree for a graph has k tree

Li Hongyan
（Department of Mathematics，Qinghai Nationalities College，Xining810007，China）

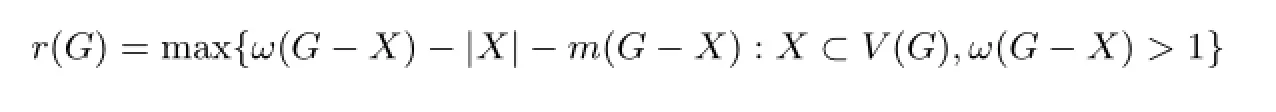
rupture degree，k-tree，induced subgraph

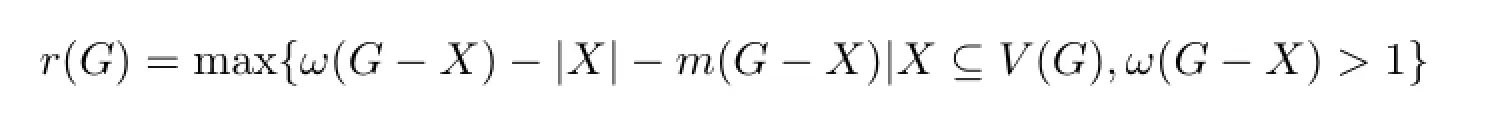
O157.5

A

1008-5513（2016）02-0127-05

10.3969/j.issn.1008-5513.2016.02.003

2015-05-08.

国家自然科学基金（11561056）.

李红燕（1977-），硕士，讲师，研究方向：图论.

其中ω（G-X）和m（G-X）分别表示G-X中的分支数目和最大分支的阶数.本文结合毁裂度给出连通图G包含一个k-树的充分条件；利用图的结构性质和毁裂度的关系逐步刻画并给出图G包含一个k-树的毁裂度条件.

2000MSC:05C15